Giải bài tập SGK Toán 11 Bài 4: Hai mặt phẳng vuông góc

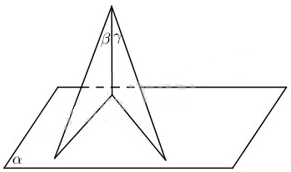
Cho ba mặt phẳng (α), (β), (γ) những mệnh đề nào sau đây đúng?

a) Nếu (α) ⊥ (β) và (α) // (γ) thì (β) ⊥ (γ).

b) Nếu (α) ⊥ (β) và (α) ⊥ (γ) thì (β) // (γ).

Phương pháp giải:

Nhận xét từng câu bằng cách vẽ phác hình, tìm phản ví dụ cho câu sai.

Hướng dẫn giải:

a) Đúng. 

Gọi m là đường thẳng vuông góc (α), n là đường thẳng vuông góc với (β).

$\Rightarrow \widehat{(\alpha ),(\beta )}=\widehat{m,n}$.

Do (α) ⊥ (β) $\Rightarrow \widehat{(\alpha ),(\beta )}=\widehat{m,n}=90^o$.

Lại có: (α) // (γ) nên m vuông góc với (γ).

$\Rightarrow\widehat{(\beta ),(\gamma )}=\widehat{m,n}=90^o$.

Vậy (β) ⊥ (γ).

b) Sai vì vẫn có thể xảy ra trường hợp hai mặt phẳng (β) và (γ) cắt nhau.

Cho hai mặt phẳng (α) và (β) vuông góc với nhau. Người ta lấy trên giao tuyến Δ của hai mặt phẳng đó hai điểm A và B sao cho AB = 8 cm. Gọi C là một điểm trên (α) và D là một điểm trên (β) sao cho AC và BD cùng vuông góc với giao tuyến Δ và AC = 6 cm, BD = 24 cm. Tính độ dài đoạn CD.

Phương pháp giải:

Chứng minh AC ⊥ AD và áp dụng định lý Pytago để tính toán.

Hướng dẫn giải:

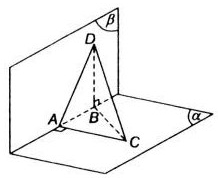
Ta có:

$\left. \matrix{ (\alpha ) \bot (\beta ) \hfill \cr AC \bot \Delta \hfill \cr AC \subset (\alpha ) \hfill \cr} \right\} \Rightarrow AC \bot (\beta ).$

Suy ra AC ⊥ AD hay tam giác ACD vuông tại A.

Áp dụng định lí Pytago vào tam giác ACD ta có:

${CD^2} = {AC^2} + {AD^2}$ (1).

Lại có: BD vuông góc với giao tuyến nên BD ⊥ AB hay tam giác ABD vuông tại B.

 Áp dụng định lí Pytago vào tam giác ABD ta được:

${AD^2} = {AB^2} + {BD^2}$ (2).

Từ (1) và (2) suy ra ${CD^2} = {AC^2} + {AB^2} + {BD^2} = {6^2} + {8^2} + {24^2} = 676$.

$\Rightarrow DC = \sqrt {676} = 26 \ cm$.

Trong mặt phẳng (α) cho tam giác ABC vuông ở B. Một đoạn thẳng AD vuông góc với (α) tại A. Chứng minh rằng:

a) $\widehat {ABD}$ là góc giữa hai mặt phẳng (ABC) và (DBC);

b) Mặt phẳng (ABD) vuông góc với mặt phẳng (BCD);

c) HK // BC với H và K lần lượt là giao điểm của DB và DC với mặt phẳng (P) đi qua A và vuông góc với DB.

Phương pháp giải:

a) Chứng minh $\widehat {ABD}$ tạo bởi hai đường thẳng lần lượt vuông góc với giao tuyến của hai mặt phẳng (ABC) và (DBC).

b) Chứng minh (BCD) chứa một đường thẳng vuông góc với (ABD).

c) Chứng minh hai đường thẳng cùng vuông góc với đường thẳng thứ ba.

Hướng dẫn giải:

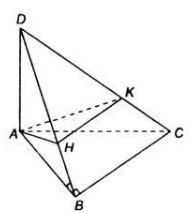
a) Ta có:

$\left\{ \begin{array}{l} AB \bot BC\ \left ( {\Delta ABC} \ vuông \ tại \ B\right)\\ AD \bot BC\ \left( {AD \bot \left( \alpha \right)} \right) \end{array} \right. \Rightarrow BC \bot \left( {ABD} \right).$

Mà BD ⊂ (ABD) suy ra BC ⊥ BD.

Lại có:

$\left\{ \begin{array}{l} \left( {ABC} \right) \cap \left( {DBC} \right) = BC\\ AB \bot BC\\ BC \bot BD \end{array} \right. \Rightarrow \left( {\widehat {\left( {ABC} \right)\left( {DBC} \right)}} \right) = \left( {\widehat {AB,BD}} \right) = \widehat {ABD}.$

b) Ta có:

$\left. \matrix{ BC \bot (ABD) (cmt) \hfill \cr BC \subset (BCD) \hfill \cr} \right\} \Rightarrow (ABD) \bot (BCD)$ (đpcm).

c) Ta có: HK ⊂ (P).

Mà (P) đi qua A và vuông góc với BD nên HK ⊥ BD.

Trong (BCD) có: HK ⊥ BD và BC ⊥ BD nên suy ra HK // BC.

Cho hai mặt phẳng (α), (β) cắt nhau và một điểm M không thuộc (α) và không thuộc (β). Chứng minh rằng qua điểm M có một và chỉ một mặt phẳng (P) vuông góc với (α) và (β). Nếu (α) song song với (β) thì kết quả trên sẽ thay đổi như thế nào?

Phương pháp giải:

Áp dụng định lí: Nếu hai mặt phẳng cắt nhau và cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba đó.

Hướng dẫn giải:

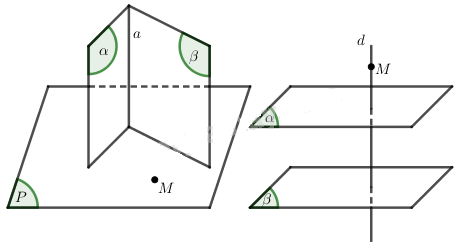
Gọi a là giao tuyến của hai mặt phẳng (α) và (β).

Ta có:

$\left\{ \begin{array}{l} \left( P \right) \bot \left( \alpha \right)\\ \left( P \right) \bot \left( \beta \right)\\ \left( \alpha \right) \cap \left( \beta \right) = a \end{array} \right. \Rightarrow a \bot \left( P \right).$

Do đó mặt phẳng (P) đi qua M và vuông góc với đường thẳng a, do đó mặt phẳng (P) là duy nhất.

Nếu (α) // (β), gọi d là đường thẳng đi qua M và vuông góc với (α) khi đó ta có d ⊥ (β).

Như vậy mọi mặt phẳng chứa d đều vuông góc với (α) và (β).

Do đó (α) // (β) thì có vô số mặt phẳng (P) đi qua M và vuông góc với (α) và (β).

Cho hình lập phương ABCD.A′B′C′D′. Chứng minh rằng:

a) Mặt phẳng (AB′C′D) vuông góc với mặt phẳng (BCD′A′);

b) Đường thẳng AC′ vuông góc với mặt phẳng (A′BD).

Phương pháp giải:

a) Chứng minh (AB′C′D) chứa một đường thẳng vuông góc với mặt phẳng (BCD′A′).

b) Chứng minh AC' vuông góc với hai đường thẳng cắt nhau trong (A'BD).

Hướng dẫn giải:

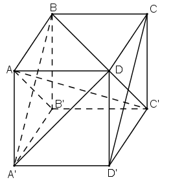
a) Ta có:

$\left\{ \begin{array}{l} BC \bot \left( {ABB'A'} \right)\ (tính \ chất \ hình \ lập \ phương)\\ AB' \subset \left( {ABB'A'} \right) \end{array} \right. \Rightarrow BC \bot AB'.$

Lại có: BA' ⊥ AB' (tính chất hình vuông).

Suy ra AB' ⊥ (BCD'A').

Mà AB′ ⊂ (AB′C′D) nên (AB′C′D) ⊥ (BCD′A′).

b) Ta có:

$\left\{ \begin{array}{l} AA' \bot BD\left(vì \ {AA' \bot \left( {ABCD} \right)} \right)\\ AC \bot BD \end{array} \right. \Rightarrow BD \bot \left( {ACC'A'} \right) \Rightarrow BD⊥AC′$ (1).

$\left\{ \begin{array}{l} AB \bot A'D\left(vì\ {AB \bot \left( {ADD'A'} \right)} \right)\\ AD' \bot A'D \end{array} \right. \Rightarrow A'D \bot \left( {ABC'D'} \right) \Rightarrow A'D \bot AC'$ (2).

Từ (1) và (2) suy ra AC' ⊥ (A'BD).

Cho hình chóp S.ABCD có đáy ABCD là một hình thoi cạnh a và có SA = SB = SC = a. Chứng minh rằng:

a) Mặt phẳng (ABCD) vuông góc với mặt phẳng (SBD);

b) Tam giác SBD là tam giác vuông.

Phương pháp giải:

a) Chứng minh (ABCD) chứa một đường thẳng vuông góc với mặt phẳng (SBD) → (ABCD) ⊥ (SBD)

b) Chứng minh tam giác SBD có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó.

Hướng dẫn giải:

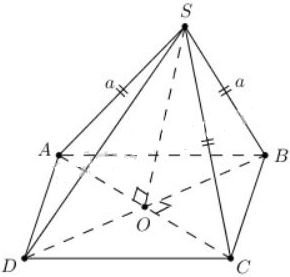
a) Gọi O là giao điểm của hai đường chéo AC và BD.

Suy ra O là trung điểm của AC, BD.

Tam giác cân SAC (vì SA = SC) có SO vừa là đường trung tuyến đồng thời là đường cao. 

=> SO ⊥ AC (1).

Lại có BD ⊥ AC (vì ABCD là hình thoi) (2).

Từ (1) và (2) suy ra AC ⊥ (SBD).

Mà $AC\subset (ABCD)\Rightarrow (ABCD)\bot (SBD)$.

b) Ta có: ΔSAC = ΔBAC (c.c.c).

Do đó các đường trung tuyến ứng với các đỉnh tương ứng của hai tam giác bằng nhau.

=> SO = BO.

Vì O là trung điểm của BD nên OB = OD = $\frac{1}{2}$.BD.

Suy ra SO=$\frac{1}{2}$.BD.

=> Tam giác SBD vuông tại S.

Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB = a, BC = b, CC′ = c.

a) Chứng minh rằng mặt phẳng (ADC′B′) vuông góc với mặt phẳng (ABB′A′).

b) Tính độ dài đường chéo AC′ theo a, b, c.

Phương pháp giải:

a) Chứng minh (ADC′B′) chứa một đường thẳng vuông góc với mặt phẳng (ABB′A′).

b) Áp dụng định lí Pytago để tính độ dài AC'.

Hướng dẫn giải:

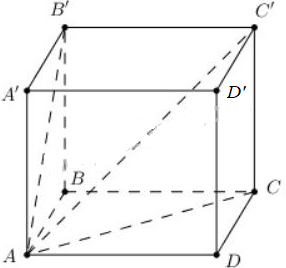
a) Ta có:

$\left\{ \begin{array}{l} DA \bot \left( {ABB'A'} \right)\\ DA \subset \left( {ADC'B'} \right) \end{array} \right. \Rightarrow \left( {ADC'B'} \right) \bot \left( {ABB'A'} \right)$.

b) Ta có:

$\left\{ \begin{array}{l} CC' \bot \left( {ABCD} \right)\\ AC \subset \left( {ABCD} \right) \end{array} \right. \Rightarrow AC \bot CC'$.

Suy ra tam giác ACC' vuông tại C, ta có:

$AC^2+CC'^2=AC'^2$ (1).

Lại có tam giác ABC vuông tại B $\Rightarrow AB^2+BC^2=AC^2$ (2).

Từ (1) và (2) suy ra:

$AC' = \sqrt {AC^2 + CC'^2} = \sqrt {AB^2 + BC^2 + CC'^2}=\sqrt{a^{2}+b^{2}+c^{2}}.$

Tính độ dài đường chéo của một hình lập phương cạnh a.

Phương pháp giải:

- Áp dụng công thức tính đường chéo của hình hộp chữ nhật có ba kích thước a, b, c là $\sqrt{a^{2}+b^{2}+c^{2}}.$

- Hình lập phương là hình hộp chữ nhật có ba kích thước bằng nhau.

Hướng dẫn giải:

Hình hộp chữ nhật có độ dài đường chéo là: $\sqrt{a^{2}+b^{2}+c^{2}}.$
Do hình lập phương có ba kích thước bằng nhau nên độ dài đường chéo của nó là: $\sqrt{a^{2}+a^{2}+a^{2}}=\sqrt{3a^2}=a\sqrt{3}$.

Cho hình chóp tam giác đều S.ABC có SH là đường cao. Chứng minh SA ⊥ BC và SB ⊥ AC.

Phương pháp giải:

- Áp dụng định nghĩa: Hình chóp đa giác đều là hình chóp có đáy là đa giác đều và chân đường cao trùng với tâm của đa giác để chứng minh SH ⊥ (ABC).

- Chứng minh BC, AC vuông góc với mặt phẳng có chứa SA, SB.

Hướng dẫn giải:

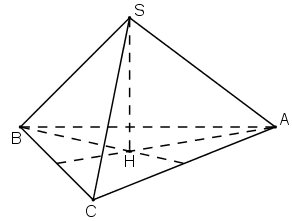
S.ABC là hình chóp tam giác đều nên H là tâm của tam giác đều ABC.

SH ⊥ (ABC) ⇒ SH ⊥ BC.

Lại có: AH ⊥ BC (vì H là trực tâm).

Suy ra BC ⊥ (SAH).

Mà SA ⊂ (SAH) ⇒ BC ⊥ SA.

Chứng minh tương tự, ta có:

SH ⊥ (ABC) ⇒ SH ⊥ AC.

Mà H là trực tâm của tam giác ABC ⇒ BH ⊥ AC.

⇒ AC ⊥ (SBH); SB ⊂ (SBH) ⇒ AC ⊥ SB.

Cho hình chóp tứ giác đều S.ABCD có các cạnh bên và cạnh đáy đều bằng a. Gọi O là tâm của hình vuông ABCD.

a) Tính độ dài đoạn thẳng SO.

b) Gọi M là trung điểm của đoạn SC. Chứng minh hai mặt phẳng (MBD) và (SAC) vuông góc với nhau.

c) Tính độ dài đoạn OM và tính góc giữa hai mặt phẳng (MBD) và (ABCD).

Phương pháp giải:

a) Áp dụng định lí Pytago để tính SO.

b) Chứng minh (MBD) chứa một đường thẳng vuông góc với (SAC).

c) Tìm hai đường thẳng lần lượt nằm trong hai mặt phẳng (MBD) và (ABCD) và vuông góc với giao tuyến.

→ Góc giữa hai mặt phẳng cần tìm là góc giữa hai đường thẳng đó.

Hướng dẫn giải:

a) Tam giác ABC vuông tại B có:

$AC=\sqrt{AB^2+BC^2}=\sqrt{a^2+a^2}=a\sqrt{2}$.

Mà O là trung điểm AC nên $OA=\frac{1}{2}.AC=a.\frac{\sqrt{2}}{2}$.

Do S.ABCD là hình chóp tứ giác đều nên SO ⊥ (ABCD) $\Rightarrow$ $SO⊥AC$.

Tam giác SOA vuông tại O có: 

$SA^2=OA^2+SO^2$

$\Rightarrow$ $SO = \sqrt{SA^{2}-AO^{2}}=\frac{a\sqrt{2}}{2}.$

b) Ta có:

$\left\{ \begin{array}{l} BD \bot AC\ \left( {tính \ chất \ hình \ vuông} \right)\\ BD \bot SO\ \left( {SO \bot \left( {ABCD} \right)} \right) \end{array} \right. \Rightarrow BD \bot \left( {SAC} \right).$

Mà BD ⊂ (MBD) do đó (MBD) ⊥ (SAC).

c) Ta có: ΔSCD ∼ ΔSCB (c.c.c) $\Rightarrow$ DM = BM $\Rightarrow$ ΔBDM cân tại M.

$\Rightarrow$ OM vừa là trung tuyến đồng thời là đường cao nên OM ⊥ BD.

Ta có:  $\left. \matrix{ (MBD) \cap (ABCD) = BD \hfill \cr OM \bot BD \hfill \cr OC \bot BD \hfill \cr} \right\}$$\Rightarrow$ góc giữa hai mặt phẳng (MBD) và (ABCD) là $\widehat {MOC}$.

Trong ΔSOC vuông tại O có OM là trung tuyến ứng với cạnh huyền SC suy ra: $OM=MC=\frac{SC}{2}=\frac{a}{2}$ hay tam giác OMC vuông cân tại M.

Nên $(\widehat{(MBD);(ABCD)})=(\widehat{MOC})=45^{o}.$

Cho hình chóp S.ABCD có đáy ABCD là một hình thoi tâm I cạnh a và có góc A bằng $60^o$, cạnh $SC=\frac{a\sqrt{6}}{2}$ và SC vuông góc với mặt phẳng (ABCD).

a) Chứng minh mặt phẳng (SBD) vuông góc với mặt phẳng (SAC). 

b) Trong tam giác SCA kẻ IK vuông góc với SA tại K. Hãy tính độ dài IK.

c) Chứng minh $\widehat{BKD}=90^{o}$ và từ đó suy ra mặt phẳng (SAB) vuông góc với mặt phẳng (SAD).

Phương pháp giải:

a) Chứng minh mặt phẳng (SBD) chứa một đường thẳng vuông góc với mặt phẳng (SAC). 

b) Chứng minh tam giác SCA và IKA đồng dạng, từ đó suy ra tỉ số các cạnh và tính IK.

c) Chứng minh tam giác BKD có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy → $\widehat{BKD}=90^{o}$.

Xác định góc giữa hai mặt phẳng (SAB) và (SAD) và chứng minh góc đó bằng $90^o$.

Hướng dẫn giải:

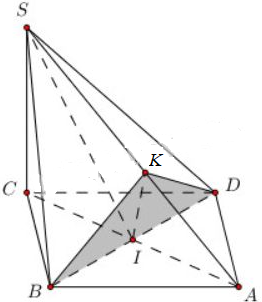
a) Ta có:

$\left\{ \begin{array}{l} SC{\rm{ }} \bot {\rm{ }}BD{\rm{ }}\ \left( {SC{\rm{ }} \bot {\rm{ }}\left( {ABCD} \right)} \right)\\ AC{\rm{ }} \bot {\rm{ }}BD\;(ABCD \ là \ hình \ thoi) \end{array} \right.$$\Rightarrow$ BD ⊥ (SAC).

Mà BD ⊂ (SBD) ⇒ (SBD) ⊥ (SAC).

b) Tam giác vuông ABI có: $cos\widehat{IAB}=\frac{AI}{AB}=>AI=AB.cos\widehat{IAB}=AB.\frac{1}{2}.\widehat{IAB}$.

$\Rightarrow$ $AI=AB.\cos 30^0={{a\sqrt 3 } \over 2}\Rightarrow AC = 2AI = a\sqrt 3$.

Tam giác vuông SAC có: $SA=\sqrt {A{C^2} + S{C^2}} = \sqrt {3{a^2} + {{6{a^2}} \over 4}} =\frac{3a}{\sqrt{2}}.$

Ta có: $\Delta SCA \sim \Delta IKA (g.g)$

$\Rightarrow$ $\frac{IK}{SC}=\frac{AI}{AS}\Rightarrow IK=\frac{AI.SC}{AS}=\frac{a}{2}.$

c) Tam giác BKD có: $IK = IB = ID = \frac{a}{2}$ $\Rightarrow$ tam giác BKD vuông tại K.

Vậy $\widehat{BKD}=90^{o}.$

Ta có:

$\left\{ \begin{array}{l} SA \bot BD\\ SA \bot IK \end{array} \right. \Rightarrow SA \bot \left( {DKB} \right) \Rightarrow SA \bot DK$.

Vì: DK và BK cùng vuông góc với SA. Vậy góc $\widehat {BKD}$ là góc giữa (SAD) và (SAB) là $\widehat{BKD}=90^{o}$ ⇒ (SAD) ⊥ (SAB).