Giải bài tập SGK Toán 11 Bài 1: Đại cương về đường thẳng và mặt phẳng
Phần hướng dẫn giải bài tập SGK bài 1 Đại cương về đường thẳng và mặt phẳng sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng tìm giao điểm của đường thẳng và mặt phẳng, của mặt phẳng và mặt phẳng, chứng minh ba đường thẳng đồng quy...từ SGK Đại số và Giải tích 11 Cơ bản và Nâng cao.
Mục lục nội dung
1. Giải bài 1 trang 53 SGK Hình học 11
2. Giải bài 2 trang 53 SGK Hình học 11
3. Giải bài 3 trang 53 SGK Hình học 11
4. Giải bài 4 trang 53 SGK Hình học 11
5. Giải bài 5 trang 53 SGK Hình học 11
6. Giải bài 6 trang 54 SGK Hình học 11
7. Giải bài 7 trang 54 SGK Hình học 11
8. Giải bài 8 trang 54 SGK Hình học 11

1. Giải bài 1 trang 53 SGK Hình học 11
Cho điểm A không nằm trong mặt phẳng (α) chứa tam giác BCD. Lấy E, F là các điểm lần lượt nằm trên các cạnh AB, AC.
a) Chứng minh đường thẳng EF nằm trong mặt phẳng (ABC).
b) Khi EF và BC cắt nhau tại I, chứng minh I là điểm chung của hai mặt phẳng (BCD) và (DEF).
Phương pháp giải:
a) Chứng minh điểm E thuộc đường thẳng mà đường thẳng đó nằm trong mặt phẳng (ABC). Chứng minh tương tự với điểm F.
b) Chứng minh điểm I thuộc hai đường thẳng, mà hai đường thẳng đó lần lượt nằm trong hai mặt phẳng (BCD) và (DEF).
Hướng dẫn giải:
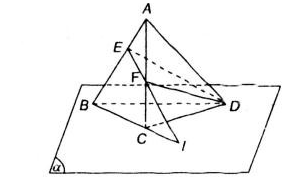
a) Ta có:
E ∈ AB ⊂ (ABC)
⇒ E ∈ (ABC).
F ∈ AC ⊂ (ABC)
⇒ F ∈ (ABC).
Đường thẳng EF có hai điểm E, F cùng thuộc (ABC) nên EF ⊂ (ABC).
b) Ta có:
I ∈ BC ⊂ (BCD) nên I ∈ (BCD) (1).
I ∈ EF ⊂ (DEF) nên I ∈ (DEF) (2).
Từ (1) và (2) suy ra I là điểm chung của hai mặt phẳng (BCD) và (DEF).
2. Giải bài 2 trang 53 SGK Hình học 11
Gọi M là giao điểm của đường thẳng d và mặt phẳng (α). Chứng minh M là điểm chung của (α) với một mặt phẳng bất kì chứa d.
Phương pháp giải:
Gọi (β) là mặt phẳng bất kì chứa d, ta chứng minh M ∈ (α) và M ∈ (β).
⇒ M là điểm chung của (α) với một mặt phẳng bất kì chứa d.
Hướng dẫn giải:
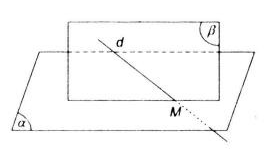
Gọi (β) là mặt phẳng bất kì chứa đường thẳng d.
Ta có \(M = d \cap \left( \alpha \right) \Rightarrow \left\{ \begin{array}{l} M \in d\\ M \in \left( \alpha \right) \ \ (1) \end{array} \right.\)
Mà d ⊂ (β) ⇒ M ∈ (β) (2).
Từ (1) và (2) suy ra M là điểm chung của (α) và (β).
Vậy M là điểm chung của (α) với một mặt phẳng bất kì chứa d.
3. Giải bài 3 trang 53 SGK Hình học 11
Cho ba đường thẳng \({d_1}\), \(d_2\), \(d_3\) không cùng nằm trong một mặt phẳng và cắt nhau từng đôi một. Chứng minh ba đường thẳng trên đồng quy.
Phương pháp giải:
- Cách 1: Gọi I = \({d_1}\) ∩ \(d_2\), M = \({d_1}\) ∩ \(d_3\), N = \(d_2 \ ∩ \ d_3\).
Chứng minh M ≡ N ≡ I bằng phương pháp phản chứng.
- Cách 2: Gọi I = \({d_1}\) ∩ \(d_2\), \((β)=(d_1,\ d_3)\), \((γ) =(d_2, \ d_3)\)
Chứng minh I ∈ (β) ∩ (γ).
Hướng dẫn giải:
Cách 1: Gọi I = \({d_1}\) ∩ \(d_2\); (P) là mặt phẳng chứa \({d_1}\) và \(d_2\).
Gọi \(d_3\) ∩ \({d_1}\) = M; \(d_3\) ∩ \(d_2\) = N.
+ M ∈ \({d_1}\), mà \({d_1}\) ⊂ (P) ⇒ M ∈ (P).
+ N ∈ \(d_2\), mà \(d_2\) ⊂ (P) ⇒ N ∈ (P).
Nếu M ≠ N ⇒ \(d_3\) có hai điểm M, N cùng thuộc (P)
⇒ \(d_3\) ⊂ (P).
⇒ \({d_1}\); \(d_2\); \(d_3\) đồng phẳng (trái với giả thiết).
⇒ M ≡ N.
⇒ M ≡ N ≡ I.
Vậy \({d_1}\); \(d_2\); \(d_3\) đồng quy.
Cách 2:
Gọi I = \({d_1}\) ∩ \(d_2\).
Ta chứng minh I ∈ \(d_3\).
Gọi (β) là mặt phẳng chứa hai đường thẳng cắt nhau \({d_1}\) và \(d_3\).
(γ) là mặt phẳng chứa hai đường thẳng cắt nhau \(d_2\) và \(d_3\).
Do ba đường thẳng không cùng nằm trong một mặt phẳng nên (β) và (γ) phân biệt.
\(\begin{array}{l} \left\{ \begin{array}{l} {d_3} \subset \left( \beta \right)\\ {d_3} \subset \left( \gamma \right) \end{array} \right. \Rightarrow \left( \beta \right) \cap \left( \gamma \right) = {d_3}\\ I \in {d_1} \subset \left( \beta \right) \Rightarrow I \in \left( \beta \right) = \left( {{d_1},{d_3}} \right)\\ I \in {d_2} \subset \left( \gamma \right) \Rightarrow I \in \left( \gamma \right) = \left( {{d_2},{d_3}} \right) \end{array}\)
Từ đó suy ra, I ∈ (β) ∩ (γ) = \(d_3\).
4. Giải bài 4 trang 53 SGK Hình học 11
Cho bốn điểm A, B, C và D không đồng phẳng. Gọi \(G_A,\ G_B, \ G_C, \ G_D\) lần lượt là trọng tâm của các tam giác BCD, CDA, ADB, ACB. Chứng minh rằng \(AG_A, \ BG_B, \ CG_C, \ DG_D\) đồng qui.
Phương pháp giải:
- Chứng minh \(AG_A, \ BG_B, \ CG_C, \ DG_D\) cắt nhau từng đôi một. Sử dụng kết quả bài tập 3 để suy ra ba đường thẳng trên đồng quy.
Hướng dẫn giải:
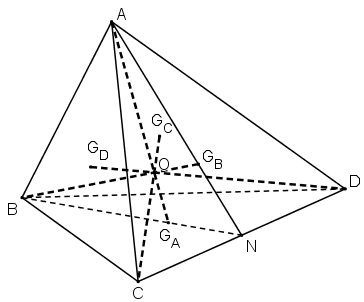
Gọi N là trung điểm CD.
Ta có \(G_A\) là trọng tâm ΔBCD.
⇒ \(G_A\) ∈ trung tuyến BN ⊂ (ANB).
⇒ \(AG_A\) ⊂ (ANB).
\(G_B\) là trọng tâm ΔACD.
⇒ \(G_B\) ∈ trung tuyến AN ⊂ (ANB).
⇒ \(BG_B\) ⊂ (ANB).
Trong (ANB): \(AG_A\) không song song với \(BG_B\).
⇒ \(AG_A\) cắt \(BG_B\) tại O.
Chứng minh tương tự: \(BG_B\) cắt \(CG_C\); \(CG_C\) cắt \(AG_A\).
\(CG_C\) không nằm trong (ANB) ⇒ \(AG_A, \ BG_B, \ CG_C\) không đồng phẳng.
⇒ \(AG_A, \ BG_B, \ CG_C\) đồng quy tại O (áp dụng kết quả bài 3).
Chứng minh hoàn toàn tương tự: \(AG_A, \ BG_B, \ DG_D\) đồng quy tại O.
Vậy \(AG_A, \ BG_B, \ CG_C, \ DG_D\) đồng quy tại O (đpcm).
5. Giải bài 5 trang 53 SGK Hình học 11
Cho tứ giác ABCD nằm trong mặt phẳng (α) có hai cạnh AB và CD không song song với nhau. S là điểm nằm ngoài mặt phẳng (α) và M là trung điểm của đoạn SC.
a) Tìm giao điểm N của đường thẳng SD và mặt phẳng (MAB).
b) Gọi O là giao điểm của AC và BD. Chứng minh rằng ba đường thẳng SO, AM và BN đồng quy.
Phương pháp giải:
a) Tìm một đường thẳng trong (MAB) cắt được SD. Khi đó giao điểm cần tìm chính là giao điểm của SD và đường thẳng đó.
b)
Cách 1: Chứng minh SO, AM và BN cắt nhau từng đôi một. Khi đó áp dụng kết quả bài tập 3 suy ra ba đường thẳng đó đồng quy.
Cách 2: Gọi I là giao điểm của AM và BN. Chứng minh I thuộc giao tuyến của hai mặt phẳng (SAC) và (SBD).
Hướng dẫn giải:
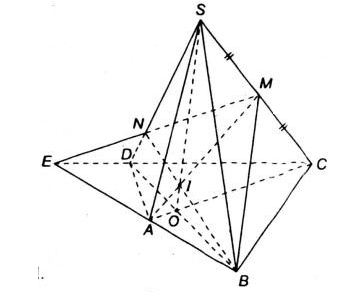
a) Trong (ABCD), gọi E là giao điểm của AB và CD, ta có:
\(\left\{ \begin{array}{l} E \in AB \subset \left( {MAB} \right) \Rightarrow {\rm{ }}E \in \left( {MAB} \right) \Rightarrow ME \subset \left( {MAB} \right)\\ E \in CD \subset \left( {SCD} \right) \Rightarrow E \in \left( {SCD} \right) \end{array} \right.\)
Mà M ∈ SC ⊂ (SCD).
⇒ ME ⊂ (SCD).
Trong (SCD), gọi N là giao điểm của ME và SD, ta có:
\(\left\{ {\begin{array}{*{20}{l}} {N \in SD}\\ {N \in EM \subset \left( {MAB} \right)} \end{array}} \right.\)
Vậy N = SD ∩ (MAB).
b) Cách 1:
Trong (SAC): SO và AM cắt nhau.
Trong (MAB) : MA và BN cắt nhau.
Trong (SBD) : SO và BN cắt nhau.
Qua AM và BN xác định được duy nhất (MAB), mà SO không nằm trong mặt phẳng (MAB) nên AM; BN; SO không đồng phẳng.
Vậy SO, MA, BN đồng quy (áp dụng kết quả bài 3).
Cách 2:
O là giao điểm của AC và BD, ta có:
\(\left\{ \begin{array}{l} O \in AC \subset \left( {SAC} \right)\\ O \in BD \subset \left( {SBD} \right) \end{array} \right. \Rightarrow O \in \left( {SAC} \right) \cap \left( {SBD} \right).\)
Lại có \(S \in \left( {SAC} \right) \cap \left( {SBD} \right).\)
Suy ra \(S O= \left( {SAC} \right) \cap \left( {SBD} \right).\)
Trong (EAN), gọi I là giao điểm của AM và BN, ta có:
\(\left\{ \begin{array}{l} I \in AM \subset \left( {SAC} \right)\\ I \in BN \subset \left( {SBD} \right) \end{array} \right. \Rightarrow I \in \left( {SAC} \right) \cap \left( {SBD} \right).\)
Suy ra I \(\in\) SO.
Vậy SO, MA, BN đồng quy tại I.
6. Giải bài 6 trang 54 SGK Hình học 11
Cho bốn điểm A, B, C và D không đồng phẳng. Gọi M và N lần lượt là trung điểm của các đoạn thẳng AC và BC. Trên đoạn BD lấy điểm P sao cho BP = 2PD.
a) Tìm giao điểm của đường thẳng CD và mặt phẳng (MNP).
b) Tìm giao tuyến của hai mặt phẳng (MNP) và (ACD).
Phương pháp giải:
a) Tìm một đường thẳng trong (NMP) cắt được CD. Khi đó giao điểm cần tìm chính là giao điểm của CD và đường thẳng đó.
b) Tìm một đường thẳng trong (MNP) và một đường thẳng trong (ACD) có thể cắt nhau tại một điểm.
→ Điểm đó chính là điểm chung của (IBC) và (DMN).
Hướng dẫn giải:
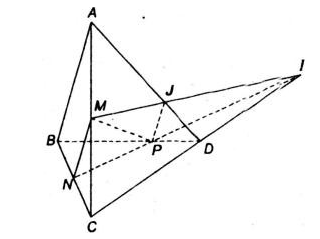
a) Ta có: \(\frac{{BN}}{{BC}} = \frac{1}{2};\frac{{BP}}{{BD}} = \frac{2}{3} \Rightarrow \frac{{BN}}{{BC}} \ne \frac{{BP}}{{BD}}\)
⇒ NP và CD không song song với nhau.
Gọi giao điểm NP và CD là I, ta có:
\(\left\{ \begin{array}{l} I \in NP \subset \left( {MNP} \right)\\ I \in CD \end{array} \right.\)
Vậy I = CD ∩ (MNP).
b) Trong (ACD), gọi J là giao điểm của AD và MI, ta có:
\(\left\{ {\begin{array}{*{20}{l}} {J \in AD \Rightarrow J \in \left( {ACD} \right)}\\ {J \in MI \Rightarrow J \in \left( {MNP} \right)} \end{array}} \right. \Rightarrow J \in \left( {ACD} \right) \cap \left( {MNP} \right)\).
Lại có: \(M \in \left( {ACD} \right) \cap \left( {MNP} \right)\).
Vậy MJ = (ACD) ∩ (MNP).
7. Giải bài 7 trang 54 SGK Hình học 11
Cho bốn điểm A, B, C và D không đồng phẳng. Gọi I, K lần lượt là trung điểm của AD và BC.
a) Tìm giao tuyến của hai mặt phẳng (IBC) và (KAD).
b) Gọi M và N là hai điểm lần lượt lấy trên hai đoạn thẳng AB và AC. Tìm giao tuyến của hai mặt phẳng (IBC) và (DMN).
Phương pháp giải:
a) Tìm hai điểm chung của hai mặt phẳng (IBC) và (KAD).
b) Tìm một đường thẳng trong (IBC) và một đường thẳng trong (DMN) có thể cắt nhau tại một điểm.
→ Điểm đó chính là điểm chung của (IBC) và (DMN).
Tương tự với điểm chung thứ hai.
Hướng dẫn giải:
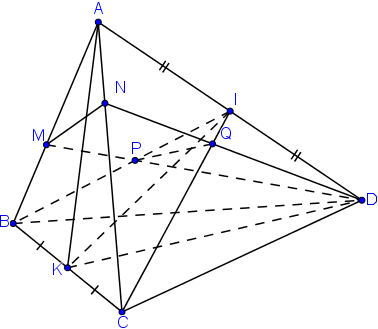
a) Ta có :
K ∈ BC ⇒ K ∈ (IBC) ⇒ K ∈ (IBC) ∩ (KAD).
I ∈ AD ⇒ I ∈ (KAD) ⇒ I ∈ (IBC) ∩ (KAD).
Vậy KI = (IBC) ∩ (KAD).
b) Trong (ABD), gọi P là giao điểm của BI và DM
⇒ P ∈ (IBC) ∩ (DMN).
Trong (ACD), gọi Q là giao điểm của CI và DN.
⇒ Q ∈ (IBC) ∩ (DMN).
Vậy (IBC) ∩ (DMN) = PQ.
8. Giải bài 8 trang 54 SGK Hình học 11
Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của các cạnh AB và CD, trên cạnh AD lấy điểm P không trùng với trung điểm của AD.
a) Gọi E là giao điểm của đường thẳng MP và đường thẳng BD. Tìm giao tuyến của hai mặt phẳng (PMN) và (BCD).
b) Tìm giao điểm của mặt phẳng (PMN) và BC.
Phương pháp giải:
a) Tìm hai điểm chung của hai mặt phẳng (PMN) và (BCD).
b) Tìm một đường thẳng trong (PMN) cắt được BC.
→ Giao điểm cần tìm chính là giao điểm của BC và đường thẳng đó.
Hướng dẫn giải:
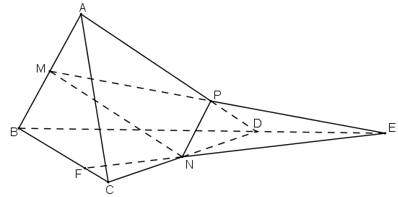
a) Trong (ABD), gọi E là giao điểm của MP và BD, ta có:
\(\left\{ \begin{array}{l} E \in MP \subset \left( {PMN} \right)\\ E \in BD \subset \left( {BCD} \right) \end{array} \right. \Rightarrow E \in \left( {PMN} \right) \cap \left( {BCD} \right).\)
Lại có: N ∈ (PMN) ∩ (BCD).
⇒ EN = (PMN) ∩ (BCD).
b) Trong (BCD), gọi giao điểm EN và BC là F, ta có:
F ∈ EN ⊂ (PMN) ⇒ F ∈ (PMN).
⇒ F = (PMN) ∩ BC.
9. Giải bài 9 trang 54 SGK Hình học 11
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Trong mặt phẳng đáy vẽ đường thẳng d đi qua A và không song song với các cạnh của hình bình hành, d cắt BC tại E. Gọi C’ là một điểm nằm trên cạnh SC.
a) Tìm giao điểm M của CD và mp(C’AE).
b) Tìm thiết diện của hình chóp cắt bởi mặt phẳng (C’AE).
Phương pháp giải:
a) Tìm một đường thẳng trong (C'AE) cắt được CD.
→ Giao điểm M chính là giao điểm của CD và đường thẳng đó.
b) Tìm giao tuyến của (P) với các mặt của khối chóp.
→ Thiết diện của một khối chóp cắt bởi mặt phẳng (P) là hình được tạo bởi các giao tuyến đó.
Hướng dẫn giải:
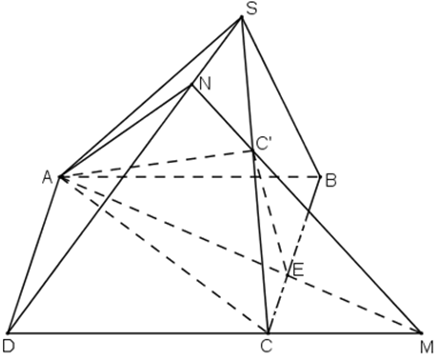
a) Trong (ABCD), d cắt CD tại M, ta có:
\(\left\{ \begin{array}{*{35}{l}} M\in CD \\ M\in d\subset \left( C'AE \right)\Rightarrow M\in \left( C'AE \right) \\ \end{array} \right. \)
Vậy M là giao điểm của CD và mp(C’AE).
b) Trong (SCD), gọi giao điểm của MC’ và SD là N, ta có:
\(\left\{ \begin{array}{*{35}{l}} N\in MC'\subset \left( C'AE \right)\Rightarrow N\text{ }\in \left( C'AE \right) \\ N\in SD\subset \left( SCD \right)\Rightarrow \text{ }N\in \left( SCD \right) \\ \end{array} \right. \)
⇒ N ∈ (C’AE) ∩ (SCD).
⇒ (C’AE) ∩ (SCD) = C’N.
Lại có:
(C’AE) ∩ (SCB) = C’E.
(C’AE) ∩ (SAD) = AN.
(C’AE) ∩ (ABCD) = AE
Vậy thiết diện của hình chóp cắt bởi mặt phẳng (C’AE) là tứ giác C’NAE.
10. Giải bài 10 trang 54 SGK Hình học 11
Cho hình chóp S.ABCD có AB và CD không song song. Gọi M là một điểm thuộc miền trong của tam giác SCD.
a) Tìm giao điểm N của đường thẳng CD và mặt phẳng (SBM).
b) Tìm giao tuyến của hai mặt phẳng (SBM) và (SAC).
c) Tìm giao điểm I của đường thẳng BM và mặt phẳng (SAC).
d) Tìm giao điểm P của SC và mặt phẳng (ABM), từ đó suy ra giao tuyến của hai mặt phẳng (SCD) và (ABM).
Phương pháp giải:
a) Tìm một đường thẳng trong (SBM) cắt được CD
→ Giao điểm N chính là giao điểm của CD và đường thẳng đó.
b) Tìm hai điểm chung của hai mặt phẳng (SBM) và (SAC).
c) Tìm một đường thẳng trong (SAC) cắt được BM
→ Giao điểm I chính là giao điểm của BM và đường thẳng đó.
d) Tìm một đường thẳng trong (ABM) cắt được SC
→ Giao điểm P chính là giao điểm của SC và đường thẳng đó.
Tìm hai điểm chung của hai mặt phẳng (SCD) và (ABM).
Hướng dẫn giải:
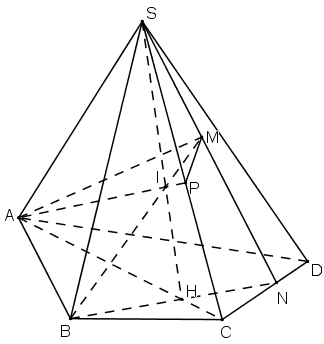
a) Trong (SCD), gọi N là giao điểm của SM và CD.
\(\Rightarrow \left\{ \begin{array}{l} N \in CD\\ N \in SM \subset \left( {SMB} \right) \end{array} \right. \Rightarrow \left( {SMB} \right) \cap CD = N\).
b) N ∈ CD ⊂ (ABCD) ⇒ BN ⊂ (ABCD).
Trong (ABCD), gọi giao điểm của AC và BN là H.
\(\left\{ \begin{array}{l} H \in AC \subset \left( {SAC} \right)\\ H{\rm{ }} \in {\rm{ }}BN{\rm{ }} \subset {\rm{ }}\left( {SBM} \right) \end{array} \right. \Rightarrow H \in \left( {SAC} \right){\rm{ }} \cap \left( {SBM} \right)\).
Lại có: \(S\in \left( {SAC} \right){\rm{ }} \cap \left( {SBM} \right)\).
⇒ (SAC) ∩ (SBM) = SH.
c) Trong (SBM), gọi giao điểm của BM và SH là I, ta có:
\(\left\{ \begin{array}{l} I \in BM\\ I \in SH \subset \left( {SAC} \right) \end{array} \right. \Rightarrow I = BM \cap \left( {SAC} \right)\).
d) Trong (SAC), gọi giao điểm của AI và SC là P, ta có:
\(\left\{ \begin{array}{l} P \in AI \subset \left( {AMB} \right)\\ P \in SC \end{array} \right. \Rightarrow P = SC \cap \left( {AMB} \right)\).
Ta có: \(P \in SC \subset \left( {SCD} \right)\).
⇒ P ∈ (AMB) ∩ (SCD).
Lại có: M ∈ (SCD) (giả thiết).
⇒ M ∈ (MAB) ∩ (SCD).
Vậy (MAB) ∩ (SCD) = MP.
Tham khảo thêm
- doc Giải bài tập SGK Toán 11 Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song
- doc Giải bài tập SGK Toán 11 Bài 3: Đường thẳng và mặt phẳng song song
- doc Giải bài tập SGK Toán 11 Bài 4: Hai mặt phẳng song song
- doc Giải bài tập SGK Toán 11 Ôn tập chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
