Giải bài tập SGK Toán 11 Bài 1: Hàm số lượng giác
Dưới đây là hướng dẫn giải bài tập SGK Toán 11 Hàm số lượng giác với nội dung gồm 8 bài tập có hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. eLib hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 11 học tập thật tốt.
Mục lục nội dung
1. Giải bài 1 trang 17 SGK Đại số & Giải tích 11
2. Giải bài 2 trang 17 SGK Đại số & Giải tích 11
3. Giải bài 3 trang 17 SGK Đại số & Giải tích 11
4. Giải bài 4 trang 17 SGK Đại số & Giải tích 11
5. Giải bài 5 trang 18 SGK Đại số & Giải tích 11
6. Giải bài 6 trang 18 SGK Đại số & Giải tích 11

1. Giải bài 1 trang 17 SGK Đại số & Giải tích 11
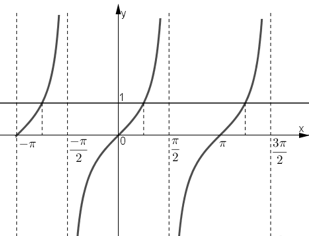
Hãy xác định các giá trị của x trên đoạn \(\small \left [- \pi ;\frac{3 \pi }{2} \right ]\) để hàm số \(\small y = tanx\)
a) Nhận giá trị bằng 0
b) Nhận giá trị bằng 1
c) Nhận giá trị dương
d) Nhận giá trị âm.
Phương pháp giải
Quan sát đồ thị hàm số, tìm các điểm thỏa mãn yêu cầu bài toán.
Hướng dẫn giải
Câu a:
Trong đoạn \(\displaystyle\left[ { - \pi ;{{3\pi } \over 2}} \right]\),
Trục hoành cắt đồ thị hàm số \(y = \tan x\) tại ba điểm có hoành độ \(- π ; 0 ; π\).
Vậy \(x = - π; x = 0 ; x = π\).
Câu b:
Đường thẳng \(y = 1\) cắt đồ thị \(y = \tan x\) tại ba điểm có hoành độ \(\displaystyle {\pi \over 4};{\pi \over 4} \pm \pi \).
Vậy \(\displaystyle x = - {{3\pi } \over 4};\,\,x = {\pi \over 4};\,\,x = {{5\pi } \over 4}\).
Câu c:
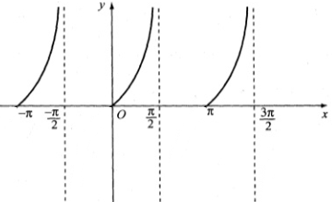
Trong các khoảng \(\displaystyle\left( { - \pi ; - {\pi \over 2}} \right)\); \(\displaystyle\left( {0;{\pi \over 2}} \right)\); \(\displaystyle \left( {\pi ;{{3\pi } \over 2}} \right)\), đồ thị hàm số nằm phía trên trục hoành.
Vậy \(\displaystyle x \in \left( { - \pi ; - {\pi \over 2}} \right) \cup \left( {0;{\pi \over 2}} \right) \cup \left( {\pi ;{{3\pi } \over 2}} \right)\)
Câu d:
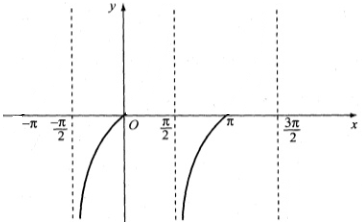
Trong các khoảng \(\displaystyle\left( { - {\pi \over 2};0} \right),\left( {{\pi \over 2};\pi } \right)\), đồ thị hàm số nằm phía dưới trục hoành.
Vậy \(\displaystyle x \in \left( { - {\pi \over 2};0} \right) \cup \left( {{\pi \over 2};\pi } \right)\).
2. Giải bài 2 trang 17 SGK Đại số & Giải tích 11
Tìm tập xác định của các hàm số
a) \(\small y=\frac{1+cosx}{sinx}\)
b) \(\small y=\sqrt{\frac{1+cosx}{1- cosx}}\)
c) \(\small y=tan(x-\frac{\pi }{3})\)
d) \(\small y=cot(x+\frac{\pi }{6})\)
Phương pháp giải
a) Hàm số có dạng \(y = \frac{A}{B}\) xác định khi và chỉ khi \(B \ne 0\).
b) Hàm số có dạng \(y = \sqrt {\frac{A}{B}} \) xác định khi và chỉ khi \(\left\{ \begin{array}{l}\frac{A}{B} \ge 0\\B \ne 0\end{array} \right.\)
c) Hàm số \(y = \tan x\) xác định khi và chỉ khi \(x \ne \frac{\pi }{2} + k\pi \,\,\left( {k \in Z} \right)\)
d) Hàm số \(y = \cot x\) xác định khi và chỉ khi \(x \ne k\pi \,\,\left( {k \in Z} \right)\)
Hướng dẫn giải
Câu a: Hàm số \(y=\frac{1+cosx}{sinx}\) xác định khi \(sinx\neq 0\Leftrightarrow x \neq k \pi,k\in \mathbb{Z}\)
Vậy tập xác định của hàm số là \(D=\mathbb{R} \setminus \left \{ k \pi,k\in \mathbb{Z} \right \}\)
Câu b: Hàm số \(y=\sqrt{\frac{1+cosx}{1-cosx}}\) xác định khi: \(\frac{{1 + \cos x}}{{1 - \cos x}} \ge 0\)
Ta thấy \(\cos x \ge - 1 \Rightarrow 1 + \cos x \ge 0\)
\(\cos x \le 1 \Rightarrow 1 - \cos x \ge 0\).
Do đó \(\frac{{1 + \cos x}}{{1 - \cos x}} \ge 0\) với mọi \(x\) thỏa mãn \(1 - \cos x \ne 0\)
\( \Leftrightarrow \cos x \ne 1\) \( \Leftrightarrow x \ne k2\pi ,k \in \mathbb{Z}\)
Vậy tập xác định của hàm số là \(D=\mathbb{R} \setminus \left \{ k 2 \pi,k\in \mathbb{Z} \right \}\)
Câu c: Hàm số xác định khi \(cos\left ( x-\frac{\pi }{3} \right )\neq 0\) \(\Leftrightarrow x-\frac{\pi }{3}\neq \frac{\pi }{2}+k\pi \Leftrightarrow x\neq \frac{5\pi }{6}+k\pi (k\in Z)\)
Vậy tập xác định của hàm số \(D=\mathbb{R} \setminus \left \{ \frac{5\pi }{6}+k \pi ,k\in Z \right \}\)
Câu d: Hàm số xác định khi \(sin \left ( x+\frac{\pi }{6} \right )\neq 0\)
\(\Leftrightarrow x+\frac{\pi }{6}\neq k\pi \Leftrightarrow x\neq -\frac{\pi }{6}+k\pi,k\in Z\)
Vậy tập xác định của hàm số là \(D=\mathbb{R} \setminus \left \{ -\frac{\pi }{6}+k \pi ,k\in Z \right \}\)
3. Giải bài 3 trang 17 SGK Đại số & Giải tích 11
Dựa vào đồ thị hàm số \(\small y = sinx\), hãy vẽ đồ thị của hàm số \(\small y = |sinx|\)
Phương pháp giải
Phương pháp vẽ đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\)
- Bước 1: Vẽ đồ thị hàm số \(y = f\left( x \right)\).
- Bước 2: Lấy đối xứng phần đồ thị phía dưới trục hoành của hàm số \(y = f\left( x \right)\) qua trục Ox.
- Bước 3: Xóa đi phần đồ thị phía dưới trục hoành của hàm số \(y = f\left( x \right)\).
Hướng dẫn giải
Ta có
\(\left| {{\mathop{\rm s}\nolimits} {\rm{inx}}} \right| = \left\{ \matrix{
{\mathop{\rm s}\nolimits} {\rm{inx}},{\mathop{\rm s}\nolimits} {\rm{inx}} \ge {\rm{0}} \hfill \cr {\rm{ - sinx}},{\mathop{\rm s}\nolimits} {\rm{inx}} \le 0 \hfill \cr} \right.\)
Bước 1: Vẽ đồ thị hàm số \(y=\sin x\).
Bước 2: Lấy đối xứng phần đồ thị phía dưới trục hoành của hàm số \(y =\sin x\) qua trục Ox.
Bước 3: Xóa đi phần đồ thị phía dưới trục hoành của hàm số \(y = \sin x\).
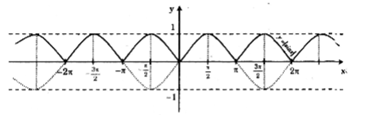
Khi đó ta được đồ thị hàm số \(y = |\sin x|\) như sau:
4. Giải bài 4 trang 17 SGK Đại số & Giải tích 11
Chứng minh rằng \(\small sin2(x + k \pi ) = sin 2x\) với mọi số nguyên k. Từ đó vẽ đồ thị hàm số \(\small y = sin2x\)
Phương pháp giải
Để vẽ được đồ thị hàm số lượng giác ta cần tìm được chu kì tuần hoàn của hàm số: \(y = \sin \left( {ax + b} \right),y = \cos \left( {ax + b} \right)\) với \(a\ne 0\) cho chu kì \(T = \frac{{2\pi }}{{\left| a \right|}}.\).
Hướng dẫn giải
Ta có \(sin2(x+k\pi)=sin(2x+2k \pi)=sin2x, k\in \mathbb{Z}\).
Từ đó suy ra hàm số y = sin2x là hàm số tuần hoàn chu kì \(\pi\), mặt khác y = sin2x là hàm số lẻ, do đó ta vẽ đồ thị hàm số y = sin2x trên \(\left [ 0;\frac{\pi }{2} \right ]\), rồi lấy đối xứng qua O ta có đồ thị trên \(\left [ -\frac{\pi }{2};\frac{\pi }{2} \right ]\) rồi sử dụng phép tịnh tiến \(\vec{v}= (\pi; 0)\) và \(-\vec{v}= (-\pi; 0)\) ta được đồ thị hàm số y = sin2x.
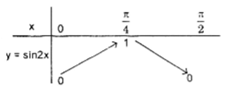
Xét y = sin2x trên \(\left [ 0;\frac{\pi }{2} \right ]\) ta có bảng biến thiên:
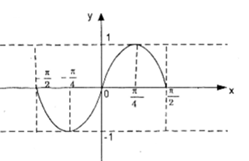
suy ra trên \(\left [ -\frac{\pi }{2};\frac{\pi }{2} \right ]\), y = sin2x có đồ thị dạng:
Do vậy đồ thị y = sin2x có dạng:
5. Giải bài 5 trang 18 SGK Đại số & Giải tích 11
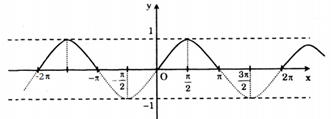
Dựa vào đồ thị hàm số y = cosx, tìm các giá trị của x để cosx = \(\frac{1}{2}\)
Phương pháp giải
\(\cos x = \dfrac{1}{2}\) là phương trình xác định hoành độ giao điểm của đường thẳng \(y= \dfrac{1}{2}\) và đồ thị \(y = \cos x\).
Hướng dẫn giải
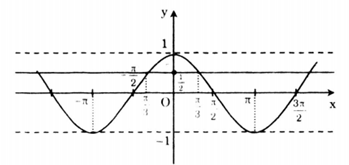
Vẽ đồ thị hàm số y = cosx và đường thẳng \(y=\frac{1}{2}\) trên cùng một hệ trục toạ độ Oxy.
Để \(cosx=\frac{1}{2}\) thì đường thẳng \(y=\frac{1}{2}\) cắt đồ thị y = cosx. Dựa vào đồ thị suy ra \(cosx=\frac{1}{2}\) khi \(x\in \left \{ ....;-\frac{7\pi }{3};-\frac{\pi }{3};\frac{\pi }{3};\frac{7\pi }{3};...\right \}\) hay \(x=\pm \frac{\pi }{3}+k2 \pi (k\in \mathbb{Z})\)
6. Giải bài 6 trang 18 SGK Đại số & Giải tích 11
Dựa vào đồ thị hàm số y = sinx, tìm các khoảng giá trị của x để hàm số đó nhận giá trị dương
Phương pháp giải
Tìm các khoảng chứa các điểm thuộc đồ thị hàm số \(y=\sin x\) và nằm phía trên trục hoành trong khoảng \([-π ; π]\) và dựa vào chu kì tuần hoàn của hàm số \(y=\sin x\) suy ra tất cả các khoảng chứa các điểm thuộc đồ thị hàm số và nằm phía trên trục hoành.
Hướng dẫn giải
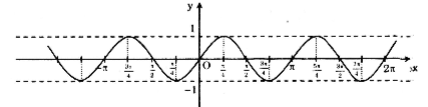
Vẽ đồ thị hàm số y = sinx.
Dựa vào đồ thị, suy ra y = sinx nhận giá trị dương khi: \(x\in \left \{ ...;(-2\pi ;-\pi );(0;\pi );(2\pi ;3\pi );... \right \}\) hay \(x\in \left \{ k2 \pi; \pi + k2 \pi \right \}\) với \(k\in \mathbb{Z}\)
7. Giải bài 7 trang 18 SGK Đại số & Giải tích 11
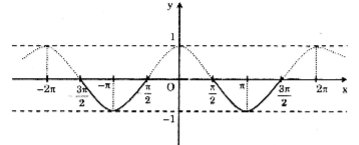
Dựa vào đồ thị hàm số y = cos x, tìm các khoảng giá trị của x để hàm số đó nhận giá trị âm
Phương pháp giải
Tìm các khoảng chứa các điểm thuộc đồ thị hàm số \(y=cosx\) và nằm phía dưới trục hoành trong khoảng \([0 ; 2π]\) và dựa vào chu kì tuần hoàn của đồ thị hàm số \(y=cosx\) suy ra tất cả các khoảng chứa các điểm thuộc đồ thị hàm số và nằm phía dưới trục hoành.
Hướng dẫn giải
Vẽ đồ thị hàm số y = cosx.
Dựa vào đồ thị hàm số, suy ra y = cosx nhận giá trị âm khi:
\(x \in \left \{ ...\left ( -\frac{7\pi}{2};-\frac{5\pi}{2} \right ); \left ( -\frac{5\pi}{3};-\frac{3\pi}{2} \right ); \left ( -\frac{3\pi}{2};-\frac{\pi}{2} \right ); \left (\frac{\pi}{2};\frac{3\pi}{2} \right ) ; \left (\frac{3\pi}{2};\frac{5\pi}{2} \right );... \right \}\)
hay \(x\in \left ( \frac{\pi }{2}+k2 \pi;\frac{3\pi}{2}+k2\pi \right ),k\in Z\)
8. Giải bài 8 trang 18 SGK Đại số & Giải tích 11
Tìm giá trị lớn nhất của hàm số
a) \(y=2\sqrt{cosx}+1\)
b) \(y=3-2sinx\)
Phương pháp giải
Sử dụng tập giá trị của hàm sin và cos: \( - 1 \le \sin x \le 1;\,\, - 1 \le \cos x \le 1\).
Hướng dẫn giải
Câu a: Ta có \(cosx \leq 1 \ \forall x.\)
\(\Rightarrow 2\sqrt{cosx}+1\leq 2.\sqrt{1}+1=3\)
⇒ max y =3 khi cosx = 1 hay khi \(x = k \pi\)
Câu b: Ta có \(sinx\geq -1 \ \ \forall x\Rightarrow 3-2sinx\leq 3+2.1=5\)
Vậy max y = 5 khi sinx = -1 hay \(x=-\frac{\pi }{2}+k2 \pi.\)