Giải bài tập SGK Toán 11 Bài 2: Hai đường thẳng vuông góc

Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa các cặp vectơ sau đây:

a) \(\overrightarrow{AB}\) và \(\overrightarrow{EG};\)

b) ​​\(\overrightarrow{AF}\) và \(\overrightarrow{EG};\)

c) \(\overrightarrow{EG}\) và \(\overrightarrow{DH}.\)

Phương pháp giải:

a) \(\left ( \overrightarrow{AB},\overrightarrow{EG} \right )=\left ( \overrightarrow{EF},\overrightarrow{EG} \right )\)

b) \(\left ( \overrightarrow{AF},\overrightarrow{EG} \right )=\left ( \overrightarrow{GD},\overrightarrow{EG} \right )\)

c) \(\left ( \overrightarrow{AB},\overrightarrow{DH} \right )=\left ( \overrightarrow{AB},\overrightarrow{AE} \right )\)

Hướng dẫn giải:

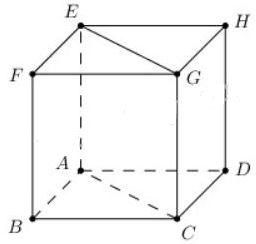
a) Ta có:

\(\overrightarrow{AB}=\overrightarrow{EF}\) \( \Rightarrow \) \(\left ( \overrightarrow{AB},\overrightarrow{EG} \right )=\left ( \overrightarrow{EF},\overrightarrow{EG} \right )=\widehat{FEG}\).

Vì EFGH là hình vuông nên \(\widehat{FEG}=45^o\).

Vậy \(\left ( \overrightarrow{AB},\overrightarrow{EG} \right )=45^o\).

b) Ta có:

\(\overrightarrow{AF}=\overrightarrow{GD}\) ​ ​\( \Rightarrow \left ( \overrightarrow{AF},\overrightarrow{EG} \right )=\left ( \overrightarrow{GD},\overrightarrow{EG} \right )=\widehat{EGD}\).

Vì EFGH, CDHG, AEHD là các hình vuông bằng nhau nên EG = GD = ED.

Suy ra tam giác EDG đều.

Vậy \((\overrightarrow{AF},\overrightarrow{EG})=60^o\).

c) Ta có:

\(\overrightarrow{DH}=\overrightarrow{AE}\)  \( \Rightarrow\left ( \overrightarrow{AB},\overrightarrow{DH} \right )=\left ( \overrightarrow{AB},\overrightarrow{AE} \right )=\widehat{EAB}\).

Mà AEFB là hình vuông nên \((\overrightarrow{AB},\overrightarrow{DH})=90^o\).

Cho hình tứ diện ABCD. 

a) Chứng minh rằng: \(\overrightarrow{AB}.\overrightarrow{CD}+\overrightarrow{AC}.\overrightarrow{DB}+\overrightarrow{AD}.\overrightarrow{BC}=0.\)

b) Từ đẳng thức trên hãy suy ra rằng nếu tứ diện ABCD có AB ⊥ CD và AC ⊥ DB thì  AD ⊥ BC. 

Phương pháp giải:

a) Áp dụng quy tắc ba điểm để chứng minh VT = VP.

b) Chứng minh \(\overrightarrow{AD}.\overrightarrow{BC}=0\Rightarrow AD ⊥ BC\).

Hướng dẫn giải:

a) Ta có:

 \(\overrightarrow{AB}.\overrightarrow{CD}=\overrightarrow{AB}.(\overrightarrow{AD}-\overrightarrow{AC})=\overrightarrow{AB}.\overrightarrow{AD}-\overrightarrow{AB}.\overrightarrow{AC}\).

\(\overrightarrow{AC}.\overrightarrow{DB}=\overrightarrow{AC}.(\overrightarrow{AB}-\overrightarrow{AD})=\overrightarrow{AC}.\overrightarrow{AB}-\overrightarrow{AC}.\overrightarrow{AD}\).

\(\overrightarrow{AD}.\overrightarrow{BC}=\overrightarrow{AD}.(\overrightarrow{AC}-\overrightarrow{AB})=\overrightarrow{AD}.\overrightarrow{AC}-\overrightarrow{AD}.\overrightarrow{AB}\).

Cộng từng vế ba đẳng thức trên ta được:

\(\overrightarrow{AB}.\overrightarrow{CD}+\overrightarrow{AC}.\overrightarrow{DB}+\overrightarrow{AD}.\overrightarrow{BC}=0\).

b) Ta có:

\(AB ⊥ CD \Rightarrow \overrightarrow{AB}.\overrightarrow{CD}=0\).

\(AC ⊥ DB \Rightarrow \overrightarrow{AC}.\overrightarrow{DB}=0\).

​\(\overrightarrow{AB}.\overrightarrow{CD}+\overrightarrow{AC}.\overrightarrow{DB}+\overrightarrow{AD}.\overrightarrow{BC}=0\)​ (cmt).

Suy ra \(\overrightarrow{AD}.\overrightarrow{BC}=0\Rightarrow AD ⊥ BC\).

a) Trong không gian nếu hai đường thẳng a và b cùng vuông góc với đường thẳng c thì a và b có song song với nhau không?

b) Trong không gian nếu đường thẳng a vuông góc với đường thẳng b và đường thẳng b vuông góc với đường thẳng c thì a có vuông góc với c không?

Phương pháp giải:

Áp dụng quan hệ vuông góc và song song giữa các đường thẳng để chỉ ra các phản ví dụ.

Hướng dẫn giải:

a) a và b chưa chắc song song vì có thể cắt nhau, chéo nhau hay vuông góc.

Ví dụ. Cho hình lập phương ABCD.A’B’C’D’ có AB và BC cùng vuông góc với BB’ nhưng AB và BC cắt nhau tại B, nghĩa là chúng không song song.

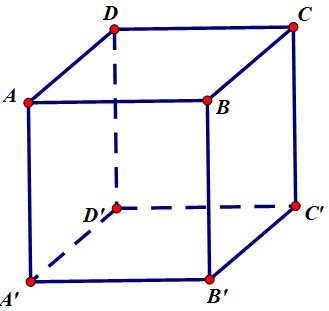
b) a và c chưa chắc vuông góc, chẳng hạn chúng có thể song song.

Ví dụ: Cho hình lập phương ABCD.A’B’C’D’ có AB và A’B’ cùng vuông góc với AA’ nhưng AB song song A'B' chứ không vuông góc.

Trong không gian cho hai tam giác đều ABC và ABC′ có chung cạnh AB và nằm trong hai mặt phẳng khác nhau. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AC, CB, B′C, C′A, Chứng minh rắng:

a) AB ⊥ CC′;

b) Tứ giác MNPQ là hình chữ nhật.

Phương pháp giải:

a) Chứng minh \(\overrightarrow{AB}.\overrightarrow{CC'}=0\) → AB ⊥ CC'.

b) Dựa vào tính chất của đường trung bình của tam giác, chứng minh MNPQ là hình bình hành, từ đó chứng minh MNPQ là hình chữ nhật.

Hướng dẫn giải:

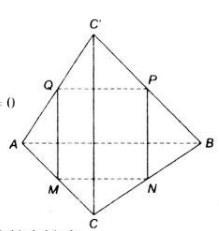
Đặt AB = a.

a) \(\overrightarrow{AB}.\overrightarrow{CC'}=\overrightarrow{AB}.(\overrightarrow{AC'}-\overrightarrow{AC})=\overrightarrow{AB}.\overrightarrow{AC'}-\overrightarrow{AB}.\overrightarrow{AC})\).

Mà \(\overrightarrow{AB}.\overrightarrow{AC'}=AB.AC'.cos\widehat{BAC'}=a.a.cos60^o\).

\(\overrightarrow{AB}.\overrightarrow{AC}=AB.AC.cos\widehat{BAC}=a.a.cos60^o\).

Suy ra \(\overrightarrow{AB}.\overrightarrow{CC'}=a.a.cos60^o-a.a.cos60^o=0\).

Vậy AB ⊥ CC′.

b) Ta có: Q, P là trung điểm của AC', BC' nên QP là đường trung bình của tam giác ABC'.

Suy ra \(QP//AB,QP={1\over 2}AB\) (1).

Chứng minh tương tự ta có:

\(PN//CC',PN={1\over 2}CC'\).

\(MN//AB,MN={1\over 2}AB\) (2).

Từ (1) và (2) suy ra \(MN//QP,MN=QP\).

Do đó MNPQ là hình bình hành.

Lại có: MN // AB, PN // CC' mà AB ⊥ CC′ do đó MN ⊥ NP.

Vậy MNPQ là hình chữ nhật.

Cho hình chóp tam giác S.ABC có SA = SB = SC và có \(\widehat{ABC}= \widehat{BSC}=\widehat{CSA}.\) Chứng minh rằng SA ⊥ BC, SB ⊥ AC, SC ⊥ AB.

Phương pháp giải:

Chứng minh \( \overrightarrow {SA} .\overrightarrow {BC} = 0\) → SA ⊥ BC.

Chứng minh tương tự với 2 trường hợp SB ⊥ AC và SC ⊥ AB.

Hướng dẫn giải:

Đặt SA = SB = SC = a, \(\widehat{ABC}= \widehat{BSC}=\widehat{CSA}=\alpha\).

\(\overrightarrow{SA}.\overrightarrow{BC}=\overrightarrow{SA}.(\overrightarrow{SC}-\overrightarrow{SB}) \\=\overrightarrow{SA}.\overrightarrow{SC}-\overrightarrow{SA}.\overrightarrow{SB} \\= SA.SC.\cos\widehat{ASC} - SA.SB.\cos\widehat{ASB} \\= a.a.cos\alpha -a.a.cos\alpha =0\)

Vậy SA ⊥ BC.

\(\overrightarrow{SB}.\overrightarrow{AC}=\overrightarrow{SB}.(\overrightarrow{SC}-\overrightarrow{SA})\\=\overrightarrow{SB}.\overrightarrow{SC}-\overrightarrow{SB}.\overrightarrow{SA} \\= SB.SC.\cos\widehat{BSC} - SB.SA.\cos\widehat{ASB} \\= a.a.cos\alpha -a.a.cos\alpha =0\)

Vậy SB ⊥ AC.

\(\overrightarrow{SC}.\overrightarrow{AB}=\overrightarrow{SC}.(\overrightarrow{SB}-\overrightarrow{SA})\\=\overrightarrow{SC}.\overrightarrow{SB}-\overrightarrow{SC}.\overrightarrow{SA} \\= SC.SB.\cos\widehat{BSC} - SC.SA.\cos\widehat{ASC} \\= a.a.cos\alpha -a.a.cos\alpha =0\)

Vậy SC ⊥ AB.

Trong không gian cho hai hình vuông ABCD và ABC′D′ có chung cạnh AB và nằm trong hai mặt phẳng khác nhau, lần lượt có tâm O và O′. Chứng minh rằng AB ⊥ OO′ và tứ giác CDD′C′ là hình chữ nhật.

Phương pháp giải:

- Chứng minh \( \overrightarrow {AB} .\overrightarrow {OO'} = 0\) → AB ⊥ OO′.

- Chứng minh tứ giác có một cặp cạnh đối song song và bằng nhau và có một góc vuông.

→ Hình chữ nhật.

Hướng dẫn giải:

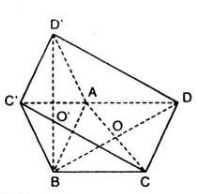
Gọi cạnh của hai hình vuông bằng nhau ABCD và ABC'D' là a.

Ta có:

\(\overrightarrow{AB}.\overrightarrow{OO'}=\overrightarrow{AB}.(\overrightarrow{AO'}-\overrightarrow{AO})\)

\(=\overrightarrow{AB}.\overrightarrow{AO'}-\overrightarrow{AB}.\overrightarrow{AO}\)

\(=AB.AO'.cos\widehat{ABO'}-AB.AO.cos\widehat{ABO}\)

\(= a.a.\cos45^{0} - a.a.\cos45^{0}=0\).

Vậy \(AB ⊥ OO'\).

\(\overrightarrow{CD}.\overrightarrow{CC'}=\overrightarrow{CD}.(\overrightarrow{AC'}-\overrightarrow{AC})\)

\(=\overrightarrow{CD}.\overrightarrow{AC'}-\overrightarrow{CD}.\overrightarrow{AC}\)

\(=CD.AC'.cos\widehat{AC'D}-CD.AC.cos\widehat{AC'D'}\)

\(= a.a.\cos45^{0} - a.a.\cos45^{0}=0\)

Suy ra \(CD \perp CC'\) (1).

Lại có: CD // C'D', CD = C'D' (do ABCD và ABC'D' là hai hình vuông bằng nhau).

Suy ra CDD'C' là hình bình hành (2).

Từ (1) và (2) suy ra CDD'C' là hình chữ nhật.

Cho S là diện tích tam giác ABC. Chứng minh rằng: \(S=\frac{1}{2}\sqrt{\overrightarrow{AB}^{2}.\overrightarrow{AC}^{2}-(\overrightarrow{AB}.\overrightarrow{AC})^{2}}.\)

Phương pháp giải:

Áp dụng các công thức:

\(\begin{array}{l} {S_{ABC}} = \frac{1}{2}.AB.AC.\sin A\\ \sin A = \sqrt {1 - {{\cos }^2}A} \\ \cos A = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}} \end{array}\)

Hướng dẫn giải:

Ta có:

\(S_{ABC}=\frac{1}{2}AB.AC.sin\widehat{A} =\frac{1}{2}AB.AC.\sqrt{1-cos^{2}\widehat{A}}\)

\(=\frac{1}{2}AB.AC.\sqrt{1-\left ( \frac{\overrightarrow{AB}.\overrightarrow{AC}}{AB.AC} \right )^{2}}\)

\(=\frac{1}{2}.AB.AC.\frac{\sqrt{\overrightarrow{AB}^{2}.\overrightarrow{AC}^{2}-(\overrightarrow{AB}.\overrightarrow{AC})^{2}}}{AB.AC}\)

\(=\frac{1}{2}\sqrt{\overrightarrow{AB}^{2}.\overrightarrow{AC}^{2}-(\overrightarrow{AB}.\overrightarrow{AC})^{2}}.\)

Cho tứ diện ABCD có AB = AC = AD và \(\widehat{BAC}=\widehat{BAD}=60^{o}.\) Chứng minh rằng: 

 a) AB ⊥ CD;

 b) Nếu M, N lần lượt là trung điểm của AB và CD thì MN ⊥ AB và MN ⊥ CD.

Phương pháp giải:

a) Chứng minh \( \overrightarrow {AB} .\overrightarrow {CD} = 0\) → AB ⊥ CD.

b) Chứng minh \( \overrightarrow {AB} .\overrightarrow {MN} = 0\) và \( \overrightarrow {MN} .\overrightarrow {CD} = 0\)

→ MN ⊥ AB và MN ⊥ CD.

Hướng dẫn giải:

Đặt AB = AC = AD = a.

a) \(\overrightarrow{AB}.\overrightarrow{CD}=\overrightarrow{AB}.(\overrightarrow{AD}-\overrightarrow{AC})=\overrightarrow{AB}.\overrightarrow{AD}-\overrightarrow{AB}.\overrightarrow{AC}\)

\(=AB.AD.\cos\widehat{BAD}-AB.AC.\cos\widehat{BAC} =a.a.cos60^o-a.a..cos60^o=0\).

Vậy AB ⊥ CD.

b) 

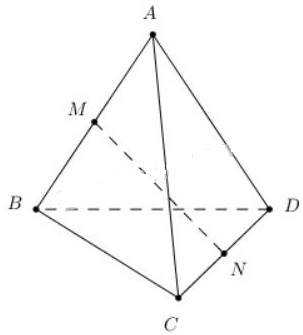
Ta có:

\(\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0}\) (M là trung điểm của AB).

\(\overrightarrow{DN}+\overrightarrow{CN}=\overrightarrow{0}\) (N là trung điểm CD).

\(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AD}+\overrightarrow{DN}\)

\(\overrightarrow{MN}=\overrightarrow{MB}+\overrightarrow{BC}+\overrightarrow{CN}\)

Suy ra

\(2.\overrightarrow{MN}=(\overrightarrow{MA}+\overrightarrow{MB})+(\overrightarrow{AD}+\overrightarrow{BC})+(\overrightarrow{DN}+\overrightarrow{CN})=\overrightarrow{AD}+\overrightarrow{BC}\)

Hay \(\overrightarrow{MN}=\frac{1}{2}(\overrightarrow{AD}+\overrightarrow{BC})=\frac{1}{2}(\overrightarrow{AD}+\overrightarrow{AC}-\overrightarrow{AB}).\)

Suy ra 

\(\overrightarrow{AB}.\overrightarrow{MN}=\frac{1}{2}.\overrightarrow {AB} .(\overrightarrow {AD} + \overrightarrow {AC} - \overrightarrow {AB} )\)

\(= {1 \over 2}(\overrightarrow{AB}.\overrightarrow{AD}+\overrightarrow{AB}.\overrightarrow{AC}-\overrightarrow{AB}^{2})\)

\(= {1 \over 2}(AB.AD.\cos\widehat{BAD}+AB.AC.\cos\widehat{BAC}-AB^2)\)

\(={1 \over 2}(a.a.\cos60^0+a.a.\cos60^0-a^2)\)

\(={1 \over 2}\left({1 \over 2}a^2+{1 \over 2}a^2-a^2\right)=0\)

\(\Rightarrow AB ⊥ MN\).

Chứng minh tương tự ra được MN ⊥ CD.