Giải bài tập SGK Toán 11 Ôn tập chương 1: Hàm số lượng giác và Phương trình lượng giác

a) Hàm số y = cos3x có phải là hàm số chẵn không? Tại sao?

b) Hàm số $y=tan\left ( x+\frac{\pi }{5} \right )$ có phải là hàm số lẻ không? Tại sao?

Phương pháp giải

- Hàm số $y = f(x)$ là hàm số chẵn nếu thỏa cả 2 điều kiện sau:

• Gọi D là tập xác định thì: $\forall x \in D$ thì $- x \in D.$
• $\forall x \in D$ thì $f( - x) = f(x).$

- Hàm số $y = f(x)$ là hàm số lẻ nếu thỏa cả 2 điều kiện sau:

• Gọi D là tập xác định thì: $\forall x \in D$ thì $- x \in D.$
• $\forall x \in D$ thì $f( - x) =  - f(x).$

Hướng dẫn giải

Câu a

Hàm số y = cos3x là hàm số chẵn. Thật vậy:

Tập xác định của hàm số: D = R.

+ $\forall x\in \mathbb{R}\Rightarrow -x\in \mathbb{R}$

+ $\forall x\in \mathbb{R}\Rightarrow y(-x) =cos(-3x)=cos3x=y(x)$

⇒ hàm số y = cos3x là hàm số chẵn.

Câu b

Hàm số $y=tan\left ( x+\frac{\pi }{5} \right )$ không phải là hàm số lẻ. Thật vậy:

Với $x=\frac{\pi }{5}\Rightarrow f(-x)=tan \left ( -\frac{\pi }{5}+\frac{\pi }{5} \right )$

$= tan 0=0\neq -f(x)=-tan\frac{2\pi }{5}$

⇒ Hàm số $y=tan\left ( x+\frac{\pi }{5} \right )$ không phải là hàm số lẻ.

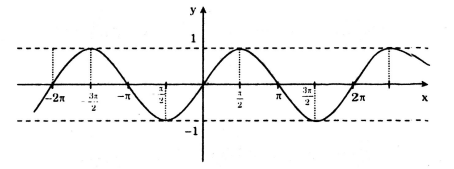
Căn cứ vào đồ thị hàm số y = sin x, tìm các giá trị của x trên đoạn $\left [ -\frac{3\pi }{2};2\pi \right ]$ để hàm số đó:

a) Nhận giá trị bằng -1

b) Nhận giá trị âm

Phương pháp giải

Vẽ đồ thị hàm số $y=sinx$ và dựa vào đồ thị hàm số.

Hướng dẫn giải

Căn cứ vào đồ thị hàm số y = sin x, trên đoạn $\left [ -\frac{3\pi }{2};2\pi \right ]$, ta có:

Câu a

sinx = -1 khi $x=-\frac{\pi }{2};x=\frac{3\pi }{2}.$

Câu b

sin x < 0 khi $x\in (-\pi ;0)\cup (\pi;2 \pi).$

Tìm giá trị lớn nhất của các hàm số

a) $y=\sqrt{2(1+cosx)}+1$

b) $y=3sin(x-\frac{\pi }{6})-2$

Phương pháp giải

Dựa vào tính chất: $- 1 \le \sin x \le 1;\,\, - 1 \le \cos x \le 1$

Hướng dẫn giải

Câu a

Ta có: $-1\leq cosx\leq 1 \ \ \ \forall x\in \mathbb{R}$

$\Rightarrow 2(1+cosx)\leq 2(1+1)=4\Rightarrow \sqrt{2(1+cosx)}+1\leq 3$

Dấu "=" xảy ra $\Leftrightarrow cosx=1\Leftrightarrow x=k2 \pi.$

Vậy Max y = 3 khi $x=k2 \pi$

Câu b

Ta có $sin\left ( x-\frac{\pi }{6} \right )\leq 1\Rightarrow 3sin \left ( x- \frac{\pi }{6} \right )-2\leq 3.1-2=1$

Dấu "=" xảy ra $\Leftrightarrow sin \left ( x-\frac{\pi }{6} \right )=1\Leftrightarrow x=\frac{2 \pi }{3}+k2 \pi.$

Vậy Max y = 1 khi $x=\frac{2 \pi}{3}+k2 \pi.$

Giải các phương trình sau

a) $sin(x+1)=\frac{2}{3}$

b) $sin^22x=\frac{1}{2}$

c) $cot^2 \frac{x}{2}=\frac{1}{3}$

d) $tan \left ( \frac{x}{12} +12x \right )=-\sqrt{3}$​

Phương pháp giải

Giải phương trình lượng giác cơ bản của hàm sin, cos, tan cot

Sử dụng công thức hạ bậc

Hướng dẫn giải

Câu a

$sin(x+1)=\frac{2}{3}$

$\Leftrightarrow \Bigg \lbrack \begin{matrix} x+1 = arcsin \frac{2}{3}+k2 \pi \ \ \ \ \ \\ \\ x+1= \pi -arcsin \frac{2}{3}+k2 \pi \end{matrix}\Leftrightarrow \Bigg \lbrack \begin{matrix} x =-1+ arcsin \frac{2}{3}+k2 \pi \ \ \ \ \ \\ \\ x= -1+\pi -arcsin \frac{2}{3}+k2 \pi \end{matrix}$

Câu b

$sin^22x=\frac{1}{2}\Leftrightarrow sin2x=\pm \frac{1}{\sqrt{2}}$

* $sin2x= \frac{1}{\sqrt{2}} \Leftrightarrow sin2x=sin\frac{\pi }{4}\Leftrightarrow \Bigg \lbrack \begin{matrix} 2x=\frac{\pi }{4}+k2\pi \ \ \\ \\ 2x=\frac{3\pi }{4}+k2\pi \ \ \end{matrix}\Leftrightarrow \Bigg \lbrack \begin{matrix} x=\frac{\pi }{8}+k\pi \ \ \\ \\ x=\frac{3\pi }{8}+k\pi \ \ \end{matrix}$

* $sin2x=- \frac{1}{\sqrt{2}} \Leftrightarrow sin2x=sin \left ( -\frac{\pi }{4} \right )\Leftrightarrow \Bigg \lbrack \begin{matrix} 2x=-\frac{\pi }{4}+k2\pi \ \ \\ \\ 2x=\frac{5\pi }{4}+k2\pi \ \ \end{matrix}\Leftrightarrow \Bigg \lbrack \begin{matrix} x=-\frac{\pi }{8}+k\pi \ \ \\ \\ x=\frac{5\pi }{8}+k\pi \ \ \end{matrix}$

Câu c

$cot^2\frac{x}{2}=\frac{1}{3}\Leftrightarrow cot \frac{x}{2}=\pm \frac{\sqrt{3}}{3}.$

* $cot \frac{x}{2}= \frac{\sqrt{3}}{3}\Leftrightarrow cot\frac{x}{2}=cot\frac{\pi}{3}\Leftrightarrow x=\frac{2\pi }{3}+k2\pi.$

* $cot \frac{x}{2}= -\frac{\sqrt{3}}{3}\Leftrightarrow cot\frac{x}{2}=cot\frac{2\pi}{3}\Leftrightarrow x=\frac{4\pi }{3}+k2\pi.$

Câu d

$tan \left ( \frac{\pi }{12} +12x\right )=-\sqrt{3}$

$tan \left (12x +\frac{\pi }{12}\right )=tan\frac{2 \pi}{3}\Leftrightarrow 12x +\frac{\pi }{12}= \frac{2 \pi}{3}+k \pi$

$\Leftrightarrow x=\frac{7 \pi}{144}+\frac{k \pi}{12}.$

Giải các phương trình sau

a) $2cos^2x – 3cosx + 1 = 0$

b) $25sin^2x + 15sin2x + 9 cos^2x = 25$

c) $2sinx + cosx = 1$

d) $sin x + 1,5cot x = 0$

Phương pháp giải

a) Đặt $t = \cos x$, đưa về phương trình bậc hai ẩn t.

b) Đưa phương trình về dạng phương trình tích.

c) Phương trình dạng $a\sin x + b\cos x = c$, chia cả 2 vế cho $\sqrt {{a^2} + {b^2}}$

d) Biến đổi, quy đồng, đưa phương trình về dạng phương trình bậc cao đối với 1 hàm số lượng giác.

Hướng dẫn giải

Câu a

$2cos^2x -3cosx + 1 = 0$

Đặt $t=cosx,- 1 \le t \le 1 \Rightarrow 2t^2-3t+1=0\Leftrightarrow \bigg \lbrack \begin{matrix} t=1\\ t=\frac{1}{2} \end{matrix}$ (Thỏa điều kiện)

* Với $t=1 \Rightarrow cosx=1\Leftrightarrow x=k 2\pi$

* Với $t=\frac{1}{2} \Rightarrow cosx=\frac{1}{2}\Leftrightarrow x= \pm \frac{\pi }{3}+k 2\pi$

Câu b

$25sin^2x + 15sin2x + 9 cos^2x = 25$  (2)

Nhận thấy $cosx =0\Leftrightarrow x=\frac{\pi }{2}+ k \pi$ là nghiệm của phương trình vì $25sin^2x=25\Leftrightarrow sin^2x =1$ luôn đúng.

Với $cosx\neq 0$. Khi đó:

$(2)\Leftrightarrow 25tan^2x + 30 tan x + 9 =25(1+tan^2 x)$

$\Leftrightarrow 30tanx=16$

$\Leftrightarrow tanx=\frac{8}{15}\Leftrightarrow x=arctan \frac{8}{15} +k \pi$

Vậy phương trình có nghiệm $x=\frac{\pi }{2}+ k \pi; x=arctan \frac{8}{15} +k \pi$

Câu c

$2sinx+cosx=1\Leftrightarrow \frac{2}{\sqrt{5}}sinx+\frac{1}{\sqrt{5}}cosx=\frac{1}{\sqrt{5}}$

Đặt $cos\alpha = \frac{2}{\sqrt{5}}; sinx =\frac{1}{\sqrt{5}}.$

Suy ra $sin(x+\alpha )=\frac{1}{\sqrt{5}}\Leftrightarrow sin(x+\alpha )= sin\alpha \Leftrightarrow \bigg \lbrack \begin{matrix} x=k 2\pi \\ x= \pi-2\alpha +k2\pi \end{matrix}$

Câu d

$sinx+1,5cotx =0$

$\Leftrightarrow sin^2x +\frac{3}{2}cosx=0\Leftrightarrow 1-cos^2x+ \frac{3}{2}cosx =0$

$\Leftrightarrow 2cos^2x-3cosx-2=0$

Đặt $t=cosx,- 1 \le t \le 1 \Rightarrow 2t^2-3t-2=0\Leftrightarrow \bigg \lbrack \begin{matrix} t=2 (loai) \\ t=-\frac{1}{2} \end{matrix}$

Với $t=-\frac{1}{2} \Rightarrow cosx=-\frac{1}{2}\Leftrightarrow cosx=cos\frac{2\pi }{3}\Leftrightarrow x=\pm \frac{3\pi }{3}+ k2\pi$

Phương trình $\cos x = \sin x$ có số nghiệm thuộc đoạn $[-π, π]$ là

(A). $2$                   (B). $4$

(C). $5$                   (D). $6$

Phương pháp giải

Đưa phương trình về dạng phương trình cơ bản của hàm tan.

Hướng dẫn giải

Ta có $cosx=sinx\Leftrightarrow sin \left ( x-\frac{\pi }{4} \right )=0 \Leftrightarrow x-\frac{\pi }{4}=k \pi\Leftrightarrow x=\frac{\pi }{4}+k\pi.$ mà $x\in [-\pi;\pi]\Rightarrow -\pi \leq \frac{\pi }{4}+k\pi\leq \pi\Leftrightarrow -\frac{5}{4}\leq k\leq \frac{3}{4}$ mà $k\in \mathbb{Z}$

$\Rightarrow k=0;k=-1$

⇒ trên [$-\pi;\pi$] phương trình có hai nghiệm.

Vậy A là đáp án cần tìm.

Phương trình ${{\cos 4x} \over {\cos 2x}} = \tan 2x$ có số nghiệm thuộc khoảng $\left( {0;\frac{\pi }{2}} \right)$ là:

A. $2$                  B. $3$

C. $4$                  D. $5$

Phương pháp giải

+) Sử dụng công thức $\tan 2x = \frac{{\sin 2x}}{{\cos 2x}}$, quy đồng, bỏ mẫu.

+) Sử dụng công thức nhân đôi: $\cos 4x = 1 - 2{\sin ^2}2x$

+) Giải phương trình bậc hai của $\sin 2x$.

+) Giải phương trình lượng giác cơ bản của hàm sin.

Hướng dẫn giải

$\frac{cos4x}{cos2x}=tan2x\Leftrightarrow cos4x=sin2x\Leftrightarrow cos4x=cos\left ( \frac{\pi }{2} -2x\right )$

$\Leftrightarrow \Bigg \lbrack \begin{matrix} 4x=\frac{\pi }{2} - 2x +k2\pi\\ \\ 4x=2x-\frac{\pi }{2} + l2\pi \end{matrix}\Leftrightarrow \Bigg \lbrack \begin{matrix} x=\frac{\pi }{12}+\frac{k\pi}{3}\\ \\ x=-\frac{\pi }{4} + l\pi \end{matrix}$

mà $x \in \left( {0;\frac{\pi }{2}} \right) \Rightarrow \left[ \begin{array}{l}0 < \frac{\pi }{{12}} + \frac{{k\pi }}{3} < \frac{\pi }{2}\\0 <  - \frac{\pi }{4} + l\pi  < \frac{\pi }{2}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l} - \frac{1}{4} < k < \frac{5}{4}\\\frac{1}{4} < l < \frac{3}{4}\end{array} \right..$

mà $k,l\in \mathbb{Z}\Rightarrow k=0, l=1.$

Phương trình có hai nghiệm thuộc $\left ( 0;\frac{\pi}{2} \right )$

Vậy (A) là đáp án cần tìm.

Nghiệm dương nhỏ nhất của phương trình $\sin x + \sin 2x = \cos x + 2 \cos^2 x$ là:

A. ${\pi  \over 6}$                B. ${{2\pi } \over 3}$

C. ${\pi  \over 4}$                D. ${\pi  \over 3}$

Phương pháp giải

Đưa phương trình về dạng tích, sau đó giải các phương trình lượng giác cơ bản, sử dụng công thức nhân đôi $\sin 2x = 2\sin x\cos x$.

Sau khi tìm được các họ nghiệm, đối với mỗi họ nghiệm ta tìm nghiệm dương nhỏ nhất và chọn đáp án đúng.

Hướng dẫn giải

$sinx+sin2x=cosx+2cos^2x$

$\Leftrightarrow (1+2cosx).sinx=cosx(1+2cosx)$

$\Leftrightarrow (2cosx+1).(sinx-cosx)=0$

$\Leftrightarrow \bigg \lbrack \begin{matrix} 2cosx +1=0\\ sinx-cosx=0 \end{matrix}\Leftrightarrow \Bigg \lbrack \begin{matrix} cosx=-\frac{1}{2}\\ \\ sin\left ( x-\frac{\pi }{4} \right )=0 \end{matrix}\Leftrightarrow \Bigg \lbrack \begin{matrix} x=\pm \frac{2\pi }{3} +k2 \pi\\ \\ x=\frac{\pi }{4}+k \pi \ \ \ \ \ \ \end{matrix}$

mà x dương nhỏ nhất suy ra: $x=\frac{\pi }{4}.$ 

Vậy (C) là đáp án cần tìm.

Nghiệm âm lớn nhất của phương trình $2{\tan ^2}x + 5\tan x + 3 = 0$ là:

A. ${{ - \pi } \over 3}$             B. ${{ - \pi } \over 4}$

C. ${{ - \pi } \over 6}$               D. ${{ - 5\pi } \over 6}$

Phương pháp giải

Giải phương trình bậc hai của hàm tan. Sau đó giải phương trình lượng giác cơ bản và biểu diễn các nghiệm trên đường tròn lượng giác.

Hướng dẫn giải

Ta có $2tan^2x+5tanx+3=0\Leftrightarrow \bigg \lbrack \begin{matrix} tanx=-1\\ tanx=-\frac{3}{4} \end{matrix}\Leftrightarrow \bigg \lbrack \begin{matrix} x=-\frac{\pi }{4} + k \pi\\ \\ x=arctan \left ( -\frac{3}{2} \right )+k \pi \end{matrix}$

Mà x là âm lớn nhất $\Rightarrow x=-\frac{\pi }{4}$

($\arctan \left( { - \frac{3}{2}} \right) \approx  - {56^0}19'$)

Vậy (B) là đáp án cần tìm.

Phương trình $2\tan x – 2 \cot x – 3 = 0$ có số nghiệm thuộc khoảng $({{ - \pi } \over 2},\pi )$ là:

A. $1$            B. $2$            C. $3$            D. $4$

Phương pháp giải

Đưa phương trình về dạng phương trình bậc hai của tanx, sử dụng công thức $\cot x = \frac{1}{{\tan x}}$.

Hướng dẫn giải

Xét phương trình: $2tan x-2cotx-3=0$

Điều kiện: $\tan x.\cot x \ne 0$

Khi đó nhân 2 vế cho $\tan x$ ta có:

$2tan x-2cotx-3=0$ $\Leftrightarrow 2tan^2x-3tanx-2=0$

$\Leftrightarrow \bigg \lbrack \begin{matrix} tanx=2\\ tanx=-\frac{1}{2} \end{matrix}\Leftrightarrow \Bigg \lbrack \begin{matrix} x=arctan 2 + k \pi\\ x = arctan \left ( -\frac{1}{2} \right )+k\pi \end{matrix}$

mà $x\in \left ( -\frac{\pi }{2}; \pi \right )\Rightarrow$ trên $\left ( -\frac{\pi }{2}; \pi \right )$ phương trình có 3 nghiệm.

Vậy (C) là đáp án cần tìm.