Giải bài tập SGK Toán 11 Bài 3: Đường thẳng và mặt phẳng song song
Nội dung giải bài tập dưới đây gồm các phương pháp và hướng dẫn giải chi tiết tương ứng cho từng bài tập, giúp các em học sinh nắm được phương pháp và rèn luyện kĩ năng giải các dạng bài tập của bài Đường thẳng và mặt phẳng song song Toán 11.
Mục lục nội dung

1. Giải bài 1 trang 63 SGK Hình học 11
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng.
a) Gọi O và O’ lần lượt là tâm của các hình bình hành ABCD và ABEF. Chứng minh rằng đường thẳng OO’ song song và các mặt phẳng (ADF) và (BCF).
b) Gọi M và N lần lượt là trọng tâm của tam giác ABD và ABE. Chứng minh đường thẳng MN song song với mặt phẳng (CEF).
Phương pháp giải:
a) Chứng minh OO' song song với đường thẳng nằm trong các mặt phẳng (ADF) và (BCF) bằng định lí đường trung bình.
b) Chứng minh MN song song với một đường thẳng nằm trong mặt phẳng (CEF) bằng định lí Talet đảo.
Hướng dẫn giải:
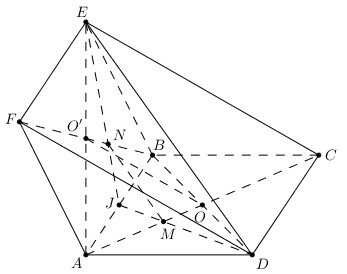
a) Ta có: các tứ giác ABCD và ABEF là các hình bình hành.
=> O là trung điểm của AC và BD và O’ là trung điểm của AE và BF. (t/c hình bình hành).
Xét tam giác BFD có OO’ là đường trung bình nên OO’ // DF.
Mà DF ⊂ (ADF) ⇒ OO' // (ADF).
Xét tam giác AEC có OO’ là đường trung bình nên OO’ // EC.
Mà EC ⊂ (BCE) ⇒ OO’ // (BCE).
b) Ta thấy mp(CEF) chính là mp(CEFD).
Gọi J là trung điểm của AB:
Ta có:
M là trọng tâm ΔABD ⇒ \(\frac{{JM}}{{JD}} = \frac{1}{3}\) (1).
N là trọng tâm ΔABE ⇒ \(\frac{{JN}}{{JE}} = \frac{1}{3}\) (2).
Từ (1) và (2) suy ra \(\frac{{JM}}{{JD}} =\frac{{JN}}{{JE}} \)
⇒ MN // DE (định lí Talet đảo).
Mà ED ⊂ (CEFD)
nên MN // (CEFD) hay MN // (CEF).
2. Giải bài 2 trang 63 SGK Hình học 11
Cho tứ diện ABCD. Trên cạnh AB lấy một điểm M. Cho (α) là mặt phẳng qua M, song song với hai đường thẳng AC và BD.
a) Tìm giao tuyến của (α) với các mặt của tứ diện.
b) Thiết diện của tứ diện cắt bởi mặt phẳng (α) là hình gì?
Phương pháp giải:
a) Tìm giao tuyến của (α) với các mặt của tứ diện bằng cách sử dụng định lí:
Cho đường thẳng a song song với mặt (α). Nếu mặt phẳng (β) chứa a cắt (α) theo giao tuyến b thì b song song với a.
b)
- Thiết diện của tứ diện cắt bởi mặt phẳng (α) là hình được tạo bởi các giao tuyến đã tìm được ở câu a.
- Xác định hình tính của thiết diện bằng các kiến thức hình học lớp 8.
Hướng dẫn giải:
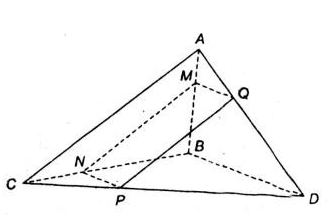
a) Ta có: (α) // AC.
⇒ Giao tuyến của (α) và (ABC) là đường thẳng song song với AC.
Mà M \(\in\) (ABC) ∩ (α).
⇒ (ABC) ∩ (α) = MN là đường thẳng qua M, song song với AC (N ∈ BC) (1).
Tương tự ta có:
(α) ∩ (ABD) = MQ là đường thẳng qua M song song với BD (Q ∈ AD) (2).
(α) ∩ (BCD) = NP là đường thẳng qua N song song với BD (P ∈ CD) (3).
(α) ∩ (ACD) = QP (4).
b) Từ (1), (2), (3) và (4) suy ra thiết diện là tứ giác MNPQ.
Ta có:
\(\left\{ \begin{array}{l} \left( \alpha \right) \cap \left( {ACD} \right) = PQ\\ AC//\left( \alpha \right)\\ AC \subset \left( {ACD} \right) \end{array} \right. \Rightarrow PQ//AC.\)
Tứ giác MNPQ có:
\(\left\{ \begin{array}{l} MQ//NP(vì \ cùng \ song \ song \ với BD)\\ MN//PQ(vì \ cùng \ song \ song \ với AC) \end{array} \right.\)
Vậy tứ giác MNPQ là hình bình hành.
3. Giải bài 3 trang 63 SGK Hình học 11
Cho hình chóp S.ABCD có đáy ABCD là một tứ giác lồi. Gọi O là giao điểm của hai đường chéo AC và BD . Xác định thiết diện của hình chóp cắt bởi mặt phẳng (α) đi qua O, song song với AB và SC. Thiết diện đó là hình gì?
Phương pháp giải:
- Tìm giao tuyến của (α) với các mặt của hình chóp.
→ Thiết diện cần tìm là hình được tạo bởi các giao tuyến đó.
- Xác định hình tính của thiết diện bằng các kiến thức hình học lớp 8.
Hướng dẫn giải:
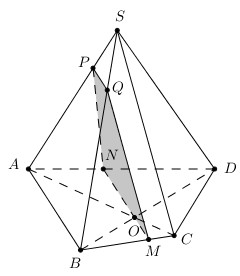
Ta có:
+ (α) // AB ⇒ giao tuyến (α) và (ABCD) song song với AB.
Mà O \(\in\) (ABCD) ∩ (α).
⇒ (ABCD) ∩ (α) = MN là đường thẳng qua O và song song với AB (M ∈ BC, N ∈ AD).
+ (α) // SC ⇒ giao tuyến của (α) và (SBC) song song với SC.
Mà M \(\in\) (SBC) ∩ (α).
⇒ (SBC) ∩ (α) = MQ là đường thẳng đi qua M và song song với SC (Q ∈ SB).
+ (α) // AB ⇒ giao tuyến của (α) và (SAB) song song với AB.
Mà Q ∈ (SAB) ∩ (α).
⇒ (SAB) ∩ (α) = QP là đường thẳng đi qua Q và song song với AB (P ∈ SA).
+ (α) ∩ (SAD) = PN.
Vậy thiết diện của hình chóp cắt bởi (α) là tứ giác MNPQ.
Ta có: PQ // AB và NM // AB.
=> PQ // NM
Vậy tứ giác MNPQ là hình thang.
Tham khảo thêm
- doc Giải bài tập SGK Toán 11 Bài 1: Đại cương về đường thẳng và mặt phẳng
- doc Giải bài tập SGK Toán 11 Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song
- doc Giải bài tập SGK Toán 11 Bài 4: Hai mặt phẳng song song
- doc Giải bài tập SGK Toán 11 Ôn tập chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
