Giải bài tập SBT Toán 11 Bài 3: Hàm số liên tục
eLib xin giới thiệu đến quý thầy cô giáo và các em học sinh nội dung giải bài tập SBT môn Hình học 11 bên dưới đây, tài liệu cung cấp cho các em hệ thống 15 bài tập trang 170, 171, 172 với đầy đủ phương pháp và hướng dẫn giải giúp các em ôn tập và hệ thống lại toàn bộ kiến thức đã học trong bài Hàm số liên tục. Mời các em tham khảo!
Mục lục nội dung
1. Giải bài 4.32 trang 170 SBT Đại số & Giải tích 11
2. Giải bài 4.33 trang 170 SBT Đại số & Giải tích 11
3. Giải bài 4.34 trang 171 SBT Đại số & Giải tích 11
4. Giải bài 4.35 trang 171 SBT Đại số & Giải tích 11
5. Giải bài 4.36 trang 171 SBT Đại số & Giải tích 11
6. Giải bài 4.37 trang 171 SBT Đại số & Giải tích 11
7. Giải bài 4.38 trang 171 SBT Đại số & Giải tích 11
8. Giải bài 4.39 trang 171 SBT Đại số & Giải tích 11
9. Giải bài 4.40 trang 171 SBT Đại số & Giải tích 11
10. Giải bài 4.41 trang 172 SBT Đại số & Giải tích 11
11. Giải bài 4.42 trang 172 SBT Đại số & Giải tích 11
12. Giải bài 4.43 trang 172 SBT Đại số & Giải tích 11
13. Giải bài 4.44 trang 172 SBT Đại số & Giải tích 11

1. Giải bài 4.32 trang 170 SBT Đại số & Giải tích 11
Cho hàm số \(f\left( x \right) = {{\left( {x - 1} \right)\left| x \right|} \over x}\)
Vẽ đồ thị của hàm số này. Từ đồ thị dự đoán các khoảng trên đó hàm số liên tục và chứng minh dự đoán đó.
Phương pháp giải:
- Đưa hàm số về dạng khoảng rồi vẽ đồ thị.
- Quan sát đồ thị nhận xét tính liên tục và kết luận.
Hướng dẫn giải:
\( f\left( x \right) = {{\left( {x - 1} \right)\left| x \right|} \over x} = \left\{ \matrix{x - 1,\,{\rm{ nếu }}\,\,x > 0 \hfill \cr 1 - x,\,{\rm{ nếu\,\, x < 0}} \hfill \cr} \right.\)
Hàm số này có tập xác định là \(R\backslash \left\{ 0 \right\}\)
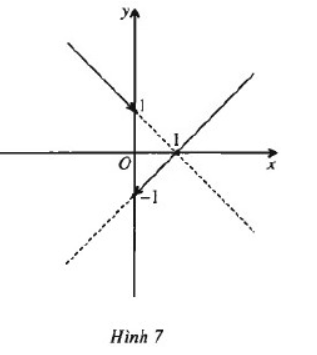
Từ đồ thị dự đoán f(x) liên tục trên các khoảng \(\left( { - \infty {\rm{ }};{\rm{ }}0} \right),\;\left( {0{\rm{ }};{\rm{ }} + \infty } \right)\) nhưng không liên tục trên R.
Thật vậy,
- Với \(x > 0, f(x) = x - 1\) là hàm đa thức nên liên tục trên R do đó liên tục trên \(\left( {0{\rm{ }};{\rm{ }} + \infty } \right)\)
- Với \(x < 0,f\left( x \right) = 1 - x\) cũng là hàm đa thức nên liên tục trên R do đó liên tục trên \(\left( { - \infty {\rm{ }};{\rm{ }}0} \right)\)
Dễ thấy hàm số gián đoạn tại x = 0 vì \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = - 1,{\rm{ }}\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = 1\)
2. Giải bài 4.33 trang 170 SBT Đại số & Giải tích 11
Cho ví dụ về một hàm số liên tục trên (a; b] và trên (b; c) nhưng không liên tục trên (a; c).
Phương pháp giải:
Lấy ví dụ hàm số dạng khoảng và chứng minh.
Hướng dẫn giải:
Xét hàm số
\( f\left( x \right) = \left\{ \matrix{ x + 2,\,{\rm{nếu}} \le {\rm{0}} \hfill \cr {1 \over {{x^2}}}{\rm\,{,nếu }}\,\,x > 0 \hfill \cr} \right.\)
- Trường hợp \(x \le 0\)
\( f\left( x \right) = x + 2\) là hàm đa thức, liên tục trên R nên nó liên tục trên (-2; 0]
- Trường hợp x > 0
\( f\left( x \right) = {1 \over {{x^2}}}\) là hàm số phân thức hữu tỉ xác định trên \(D = R\backslash \left\{ 0 \right\}\) nên liên tục trên (0; 2).
Như vậy f(x) liên tục trên (-2; 0] và trên (0; 2)
Tuy nhiên, vì \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} {1 \over {{x^2}}} = + \infty \) nên hàm số f(x) không có giới hạn hữu hạn tại x = 0.
Do đó, nó không liên tục tại x = 0.
Nghĩa là không liên tục trên (-2; 2).
3. Giải bài 4.34 trang 171 SBT Đại số & Giải tích 11
Chứng minh rằng nếu một hàm số liên tục trên (a; b] và trên [b; c) thì nó liên tục trên (a; c).
Phương pháp giải:
Chứng minh hàm số liên tục tại điểm b suy ra điều phải chứng minh
Hướng dẫn giải:
Vì hàm số liên tục trên (a; b] nên liên tục trên (a; b) và \(\mathop {\lim }\limits_{x \to {b^ - }} f\left( x \right) = f\left( b \right) \) (1)
Vì hàm số liên tục trên [b; c) nên liên tục trên (b; c) và \(\mathop {\lim }\limits_{x \to {b^ + }} f\left( x \right) = f\left( b \right) \) (2)
Từ (1) và (2) suy ra f(x) liên tục trên các khoảng (a; b), (b; c) và liên tục tại x = b (vì \(\mathop {\lim }\limits_{x \to b} f\left( x \right) = f\left( b \right) \)).
Nghĩa là nó liên tục trên (a; c).
4. Giải bài 4.35 trang 171 SBT Đại số & Giải tích 11
Cho hàm số y = f(x) xác định trên khoảng (a; b) chứa điểm x0
Chứng minh rằng nếu \(\mathop {\lim }\limits_{x \to {x_0}} {{f\left( x \right) - f\left( {{x_0}} \right)} \over {x - {x_0}}} = L\) thì hàm số f(x) liên tục tại điểm x0.
Hướng dẫn: Đặt \(g\left( x \right) = {{f\left( x \right) - f\left( {{x_0}} \right)} \over {x - {x_0}}} - L\) và biểu diễn f(x) qua g(x).
Phương pháp giải:
Đặt \(g\left( x \right) = {{f\left( x \right) - f\left( {{x_0}} \right)} \over {x - {x_0}}} - L\) và biểu diễn f(x) qua g(x).
Hướng dẫn giải:
Đặt \(g\left( x \right) = {{f\left( x \right) - f\left( {{x_0}} \right)} \over {x - {x_0}}} - L\)
Suy ra g(x) xác định trên \(\left( {a{\rm{ }};{\rm{ }}b} \right)\backslash \left\{ {{x_0}} \right\}\) và \(\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = 0\)
Mặt khác, \(f\left( x \right) = f\left( {{x_0}} \right) + L\left( {x - {x_0}} \right) + \left( {x - {x_0}} \right)g\left( x \right)\) nên
\( \eqalign{ & \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( {{x_0}} \right) + L\left( {x - {x_0}} \right) + \left( {x - {x_0}} \right)g\left( x \right)} \right] \cr & = \mathop {\lim }\limits_{x \to {x_0}} f\left( {{x_0}} \right) + \mathop {\lim }\limits_{x \to {x_0}} L\left( {x - {x_0}} \right) + \mathop {\lim }\limits_{x \to {x_0}} \left( {x - {x_0}} \right).\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = f\left( {{x_0}} \right). \cr} \)
Vậy hàm số y = f(x) liên tục tại x0.
5. Giải bài 4.36 trang 171 SBT Đại số & Giải tích 11
Xét tính liên tục của các hàm số sau:
a) \( f\left( x \right) = \sqrt {x + 5}\) tại x = 4
b) \( g\left( x \right) = \left\{ \matrix{ {{x - 1} \over {\sqrt {2 - x} - 1}},\,\,{\rm{ nếu }}\,\,x < 1 \hfill \cr - 2x{\rm{ ,\,\, nếu }}\,\,x \ge 1 \hfill \cr} \right. tại x = 1\)
Phương pháp giải:
Hàm số y = f(x) liên tục tại \({x_0} \Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Hướng dẫn giải:
a) Hàm số \(f\left( x \right) = \sqrt {x + 5}\) có tập xác định là \( {\rm{[}} - 5{\rm{ }};{\rm{ }} + \infty ). \)
Do đó, nó xác định trên khoảng \(\left( { - 5{\rm{ }};{\rm{ }} + \infty } \right)\) chứa x = 4
Vì \(\mathop {\lim }\limits_{x \to 4} f\left( x \right) = \mathop {\lim }\limits_{x \to 4} \sqrt {x + 5} = 3 = f\left( 4 \right)\) nên f(x) liên tục tại x = 4
b) Hàm số: \(g\left( x \right) = \left\{ \matrix{ {{x - 1} \over {\sqrt {2 - x} - 1}},\,\,{\rm{ nếu }}\,\,x < 1 \hfill \cr - 2x{\rm{ ,\,\, nếu }}\,\,x \ge 1 \hfill \cr} \right.\) có tập xác định là R
Ta có, \(g\left( 1 \right) = - 2 \) (1)
\( \eqalign{ & \mathop {\lim }\limits_{x \to {1^ - }} g\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} {{x - 1} \over {\sqrt {2 - x} - 1}} \cr & = \mathop {\lim }\limits_{x \to {1^ - }} {{\left( {x - 1} \right)\left( {\sqrt {2 - x} + 1} \right)} \over {1 - x}} \cr & = \mathop {\lim }\limits_{x \to {1^ - }} \left( { - \sqrt {2 - x} - 1} \right) = - 2 \ (2) \cr } \\ \mathop {\lim }\limits_{x \to {1^ + }} g\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( { - 2x} \right) = - 2 \ (3)\)
Từ (1), (2) và (3) suy ra \(\mathop {\lim }\limits_{x \to 1} g\left( x \right) = - 2 = g\left( 1 \right)\)
Vậy g(x) liên tục tại x = 1.
6. Giải bài 4.37 trang 171 SBT Đại số & Giải tích 11
Xét tính liên tục của các hàm số sau trên tập xác định của chúng:
a) \(f\left( x \right) = \left\{ \matrix{ {{{x^2} - 2} \over {x - \sqrt 2 }},\,{\rm{ nếu }}\,\,x \ne \sqrt 2 \hfill \cr 2\sqrt 2 {\rm{ , \,\,nếu }}\,\,x = \sqrt 2 \hfill \cr} \right.\)
b) \( g\left( x \right) = \left\{ \matrix{ {{1 - x} \over {{{\left( {x - 2} \right)}^2}}},\,\,{\rm{ nếu }}\,\,x \ne 2 \hfill \cr 3{\rm{ ,\,\, nếu }}\,\,x = 2 \hfill \cr} \right.\)
Phương pháp giải:
- Tìm tập xác định của hàm số.
- Hàm số y = f(x) liên tục tại \({x_0} \Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Hướng dẫn giải:
a) \( f\left( x \right) = \left\{ \matrix{ {{{x^2} - 2} \over {x - \sqrt 2 }},\,{\rm{ nếu }}\,\,x \ne \sqrt 2 \hfill \cr 2\sqrt 2 {\rm{ , \,\,nếu }}\,\,x = \sqrt 2 \hfill \cr} \right. \)
Tập xác định của hàm số là D = R
- Nếu \(x \ne \sqrt 2 \) thì \(f\left( x \right) = {{{x^2} - 2} \over {x - \sqrt 2 }}\)
Đây là hàm phân thức hữu tỉ nên liên tục trên các khoảng \(\left( { - \infty {\rm{ }};{\rm{ }}\sqrt 2 } \right)\) và \(\left( {\sqrt 2 {\rm{ }};{\rm{ }} + \infty } \right)\)
- Tại \(x = \sqrt 2 \):
\( \eqalign{ & \mathop {\lim }\limits_{x \to \sqrt 2 } f\left( x \right) = \mathop {\lim }\limits_{x \to \sqrt 2 } {{{x^2} - 2} \over {x - \sqrt 2 }} \cr & = \mathop {\lim }\limits_{x \to \sqrt 2 } {{\left( {x - \sqrt 2 } \right)\left( {x + \sqrt 2 } \right)} \over {x - \sqrt 2 }} \cr & = \mathop {\lim }\limits_{x \to \sqrt 2 } \left( {x + \sqrt 2 } \right) = 2\sqrt 2 = f\left( {\sqrt 2 } \right) \cr}\)
Vậy hàm số liên tục tại \(x = \sqrt 2 \).
Kết luận: y = f(x) liên tục trên R.
b) \(g\left( x \right) = \left\{ \matrix{ {{1 - x} \over {{{\left( {x - 2} \right)}^2}}},\,\,{\rm{ nếu }}\,\,x \ne 2 \hfill \cr 3{\rm{ ,\,\, nếu }}\,\,x = 2 \hfill \cr} \right.\)
Tập xác định là D = R
- Nếu \(x \ne 2\) thì \(g\left( x \right) = {{1 - x} \over {{{\left( {x - 2} \right)}^2}}}\) là hàm phân thức hữu tỉ, nên nó liên tục trên các khoảng \(\left( { - \infty ,2} \right)\) và \(\left( {2, + \infty } \right)\)
Tại x = 2: \(\mathop {\lim }\limits_{x \to 2} g\left( x \right) = \mathop {\lim }\limits_{x \to 2} {{1 - x} \over {{{\left( {x - 2} \right)}^2}}} = - \infty\)
Vậy hàm số y = g(x) không liên tục tại x = 2
Kết luận: y = g(x) liên tục trên các khoảng \(\left( { - \infty ,2} \right)\) và \(\left( {2, + \infty } \right)\) nhưng gián đoạn tại x = 2.
7. Giải bài 4.38 trang 171 SBT Đại số & Giải tích 11
Tìm giá trị của tham số m để hàm số \( f\left( x \right) = \left\{ \matrix{ {{\sqrt x - 1} \over {{x^2} - 1}},\,\,{\rm{ nếu }}\,\,x \ne 1 \hfill \cr {m^2}{\rm{ ,\,\, nếu }}\,\,x = 1 \hfill \cr} \right. \) liên tục trên \(\left( {0; + \infty } \right) .\)
Phương pháp giải:
Hàm số y = f(x) liên tục tại \({x_0} \Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Hướng dẫn giải:
Trên \(\left( {0; + \infty } \right)\backslash \left\{ 1 \right\}\) thì \(f\left( x \right) = \dfrac{{\sqrt x - 1}}{{{x^2} - 1}}\) là hàm phân thức nên liên tục.
Tại x = 1 ta có:
\( \begin{array}{l}\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} \dfrac{{\sqrt x - 1}}{{{x^2} - 1}}\\ = \mathop {\lim }\limits_{x \to 1} \dfrac{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}{{\left( {{x^2} - 1} \right)\left( {\sqrt x + 1} \right)}}\\ = \mathop {\lim }\limits_{x \to 1} \dfrac{{x - 1}}{{\left( {x - 1} \right)\left( {x + 1} \right)\left( {\sqrt x + 1} \right)}}\\ = \mathop {\lim }\limits_{x \to 1} \dfrac{1}{{\left( {x + 1} \right)\left( {\sqrt x + 1} \right)}}\\ = \dfrac{1}{{\left( {1 + 1} \right)\left( {\sqrt 1 + 1} \right)}} = \dfrac{1}{4}\end{array}\)
Để hàm số liên tục trên \(\left( {0; + \infty } \right)\) thì nó liên tục tại x = 1
\( \Leftrightarrow \mathop {\lim }\limits_{x \to 1} f\left( x \right) = f\left( 1 \right) \\ \Leftrightarrow \dfrac{1}{4} = {m^2} \Leftrightarrow m = \pm \dfrac{1}{2}\)
Vậy \(m = \pm \dfrac{1}{2} .\)
8. Giải bài 4.39 trang 171 SBT Đại số & Giải tích 11
Chứng minh rằng phương trình:
a) \({x^5} - 3x - 7 = 0\) luôn có nghiệm;
b) \( \cos 2x = \sin x - 2\) có ít nhất hai nghiệm trong khoảng \(\left( { - {\pi \over 6};\pi } \right) \);
c) \( \sqrt {{x^3} + 6x + 1} - 2 = 0\) có nghiệm dương.
Phương pháp giải:
a) Chọn [a;b] sao cho f(a).f(b) < 0 ⇒ Phương trình f(x) có nghiệm thuộc [a; b].
b) Chọn [a;b] và [c; d] sao cho f(a).f(b) < 0, f(c).f(d) < 0 ⇒ Phương trình f(x) có nghiệm thuộc [a; b], [c; d].
c) Chọn [a;b] \((0\le a<b)\) sao cho f(a).f(b) < 0 ⇒ Phương trình f(x) có nghiệm thuộc [a; b].
Hướng dẫn giải:
a) Hàm số \(f\left( x \right) = {x^5} - 3x - 7\) liên tục trên R nên liên tục trên \(\left[ {0;2} \right]\)
Ta có: \(f\left( 0 \right) = - 7,f\left( 2 \right) = 19 \Rightarrow f\left( 0 \right).f\left( 2 \right) < 0\)
Vậy phương trình f(x) = 0 luôn có ít nhất một nghiệm thuộc \(\left( {0;2} \right) .\)
b) Hàm số \(f\left( x \right) = \cos 2x - 2\sin x + 2\) liên tục trên R nên liên tục trên \(\left[ { - \dfrac{\pi }{6};\dfrac{\pi }{2}} \right]\) và \(\left[ {\dfrac{\pi }{2};\pi } \right]\)
Ta có:
\( f\left( { - \dfrac{\pi }{6}} \right) = \cos \left( { - \dfrac{\pi }{3}} \right) - 2\sin \left( { - \dfrac{\pi }{6}} \right) + 2 = \dfrac{7}{2} \\ f\left( {\dfrac{\pi }{2}} \right) = - 1 \\ f\left( \pi \right) = 3\)
\( \Rightarrow f\left( { - \dfrac{\pi }{6}} \right).f\left( {\dfrac{\pi }{2}} \right) < 0\) nên phương trình \(f\left( x \right) = 0\) có ít nhất một nghiệm thuộc \(\left( { - \dfrac{\pi }{6};\dfrac{\pi }{2}} \right) .\)
\( f\left( {\dfrac{\pi }{2}} \right).f\left( \pi \right) < 0\) nên phương trình \(f\left( x \right) = 0\) có ít nhất một nghiệm thuộc \(\left( {\dfrac{\pi }{2};\pi } \right) .\)
Vậy phương trình \(f\left( x \right) = 0\) có ít nhất hai nghiệm thuộc \(\left( { - \dfrac{\pi }{6};\pi } \right) .\)
c) Ta có:
\( \eqalign{ & \sqrt {{x^3} + 6x + 1} - 2 = 0 \cr & \Leftrightarrow {x^3} + 6x + 1 = 4 \cr & \Leftrightarrow {x^3} + 6x - 3 = 0 \cr}\)
Hàm số \(f(x)={x^3} + 6x - 3\) liên tục trên R nên liên tục trên đoạn [0; 1] (1)
Ta có \(f\left( 0 \right)f\left( 1 \right) = - 3.4 < 0 \) (2)
Từ (1) và (2) suy ra phương trình \({x^3} + 6x - 3 = 0\) có ít nhất một nghiệm thuộc (0; 1)
Do đó, phương trình \(\sqrt {{x^3} + 6x + 1} - 2 = 0\) có ít nhất một nghiệm dương.
9. Giải bài 4.40 trang 171 SBT Đại số & Giải tích 11
Chứng minh các phương trình sau luôn có nghiệm với mọi giá trị của tham số m:
a) \( \left( {1 - {m^2}} \right){\left( {x + 1} \right)^3} + {x^2} - x - 3 = 0\)
b) \(m\left( {2\cos x - \sqrt 2 } \right) = 2\sin 5x + 1\)
Phương pháp giải:
Chọn [a;b] sao cho f(a).f(b) < 0 với mọi giá trị m ⇒ Phương trình f(x) có nghiệm thuộc [a; b].
Hướng dẫn giải:
a) \( \left( {1 - {m^2}} \right){\left( {x + 1} \right)^3} + {x^2} - x - 3 = 0 \)
\( f\left( x \right) = \left( {1 - {m^2}} \right){\left( {x + 1} \right)^3} + {x^2} - x - 3\) là hàm đa thức liên tục trên R. Do đó nó liên tục trên [-2; -1]
Ta có \(f\left( { - 1} \right) = - 1 < 0\) và \(f\left( { - 2} \right) = {m^2} + 2 > 0\) nên \(f\left( { - 1} \right)f\left( { - 2} \right) < 0\) với mọi m.
Do đó, phương trình \(f\left( x \right) = 0\) luôn có ít nhất một nghiệm trong khoảng (-2; -1) với mọi m.
Vậy phương trình \(\left( {1 - {m^2}} \right){\left( {x + 1} \right)^3} + {x^2} - x - 3 = 0\) luôn có nghiệm với mọi m.
b) \(m\left( {2\cos x - \sqrt 2 } \right) = 2\sin 5x + 1\)
Xét hàm số \(f\left( x \right) = m\left( {2\cos x - \sqrt 2 } \right) - 2\sin 5x - 1\) trên đoạn \(\left[ { - {\pi \over 4};{\pi \over 4}} \right] .\)
Hàm số \(f\left( x \right) = m\left( {2\cos x - \sqrt 2 } \right) - 2\sin 5x - 1\) là hàm số lượng giác có TXĐ D = R
⇒ Liên tục trên \(\left[ { - \dfrac{\pi }{4};\dfrac{\pi }{4}} \right]\)
Ta có:
\( f\left( { - \dfrac{\pi }{4}} \right) = m\left( {2\cos \left( { - \dfrac{\pi }{4}} \right) - \sqrt 2 } \right) - 2\sin \left( { - \dfrac{{5\pi }}{4}} \right) - 1 = - 1 - \sqrt 2 < 0 \\ f\left( {\dfrac{\pi }{4}} \right) = m\left( {2\cos \left( {\dfrac{\pi }{4}} \right) - \sqrt 2 } \right) - 2\sin \left( {\dfrac{{5\pi }}{4}} \right) - 1 = - 1 + \sqrt 2 > 0 \\ \Rightarrow f\left( { - \dfrac{\pi }{4}} \right).f\left( {\dfrac{\pi }{4}} \right) < 0\)
Vậy phương trình \(f\left( x \right) = 0\) có ít nhất một nghiệm trong khoảng \(\left( { - \dfrac{\pi }{4};\dfrac{\pi }{4}} \right)\) với mọi m .
10. Giải bài 4.41 trang 172 SBT Đại số & Giải tích 11
Chứng minh phương trình \( {x^n} + {a_1}{x^{n - 1}} + {a_2}{x^{n - 2}} + ... + {a_{n - 1}}x + {a_n} = 0\) luôn có nghiệm với n là số tự nhiên lẻ.
Phương pháp giải:
Hàm số y = f(x) xác định và liên tục trên (a; b). Nếu \(f\left( a \right).f\left( b \right) < 0\) thì tồn tại ít nhất một số \(c \in \left( {a;b} \right)\) sao cho\( f\left( c \right) = 0 .\)
Hướng dẫn giải:
Hàm số \(f\left( x \right) = {x^n} + {a_1}{x^{n - 1}} + {a_2}{x^{n - 2}} + ... + {a_{n - 1}}x + {a_n}\) xác định trên R
Ta có
\( \eqalign{ & \mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {{x^n} + {a_1}{x^{n - 1}} + {a_2}{x^{n - 2}} + ... + {a_{n - 1}}x + {a_n}} \right) \cr & {\rm{ = }}\mathop {\lim }\limits_{x \to + \infty } {x^n}\left( {1 + {{{a_1}} \over x} + {{{a_2}} \over {{x^2}}} + ... + {{{a_{n - 1}}} \over {{x^{n - 1}}}} + {{{a_n}} \over {{x^n}}}} \right) = + \infty \cr}\)
Vì \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty \) nên với dãy số \(\left( {{x_n}} \right)\) bất kì mà \({x_n} \to + \infty \) ta luôn có \(\lim f\left( {{x_n}} \right) = + \infty\)
Do đó, \(f\left( {{x_n}} \right)\) có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Nếu số dương này là 1 thì \(f\left( {{x_n}} \right) > 1\) kể từ một số hạng nào đó trở đi.
Nói cách khác, luôn tồn tại số a sao cho \(f\left( a \right) > 1 \) (1)
\( \eqalign{ & \mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to - \infty } \left( {{x^n} + {a_1}{x^{n - 1}} + {a_2}{x^{n - 2}} + ... + {a_{n - 1}}x + {a_n}} \right) \cr & {\rm{ = }}\mathop {\lim }\limits_{x \to - \infty } {x^n}\left( {1 + {{{a_1}} \over x} + {{{a_2}} \over {{x^2}}} + ... + {{{a_{n - 1}}} \over {{x^{n - 1}}}} + {{{a_n}} \over {{x^n}}}} \right) = - \infty \cr} \)
(do n lẻ)
Vì \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - \infty\) nên với dãy số \(\left( {{x_n}} \right)\) bất kì mà \({x_n} \to - \infty \) ta luôn có \(\lim f\left( {{x_n}} \right) = - \infty \) hay \(\lim \left[ { - f\left( {{x_n}} \right)} \right] = + \infty\)
Do đó, \(- f\left( {{x_n}} \right)\) có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Nếu số dương này là 1 thì \( - f\left( {{x_n}} \right) > 1\) kể từ số hạng nào đó trở đi.
Nói cách khác, luôn tồn tại b sao cho \( - f\left( b \right) > 1 \ hay \ f\left( b \right) < - 1 \) (2)
Từ (1) và (2) suy ra \(f\left( a \right)f\left( b \right) < 0\)
Mặt khác, f(x) hàm đa thức liên tục trên R nên liên tục trên [a; b]
Do đó, phương trình f(x) = 0 luôn có nghiệm.
11. Giải bài 4.42 trang 172 SBT Đại số & Giải tích 11
Cho hàm số y = f(x) liên tục trên đoạn [a; b]. Nếu \(f\left( a \right).f\left( b \right) > 0\) thì phương trình \(f\left( x \right) = 0\) có nghiệm hay không trong khoảng (a; b)? Cho ví dụ minh hoạ.
Phương pháp giải:
Lấy ví dụ một phương trình đơn giản và nhận xét.
Hướng dẫn giải:
Nếu hàm số y = f(x) liên tục trên đoạn [a; b] và \(f\left( a \right).f\left( b \right) > 0\) thì phương trình f(x) = 0 có thể có nghiệm hoặc vô nghiệm trong khoảng (a; b)
Ví dụ minh hoạ:
+ \(f\left( x \right) = {x^2} - 1\) liên tục trên đoạn \(\left[ { - 2;2} \right],f\left( { - 2} \right)f\left( 2 \right) = 9 > 0\)
Phương trình \({x^2} - 1 = 0\) có nghiệm \(x = \pm 1\) trong khoảng (-2; 2)
+ \(f\left( x \right) = {x^2} + 1\) liên tục trên đoạn [-1; 1] và \(f\left( { - 1} \right)f\left( 1 \right) = 4 > 0 \). Còn phương trình \({x^2} + 1 = 0\) lại vô nghiệm trong khoảng (-1; 1).
12. Giải bài 4.43 trang 172 SBT Đại số & Giải tích 11
Nếu hàm số y = f(x) không liên tục trên đoạn [a; b] nhưng \(f\left( a \right)f\left( b \right) < 0\) thì phương trình \(f\left( x \right) = 0\) có nghiệm hay không trong khoảng (a; b)? Hãy giải thích câu trả lời bằng minh hoạ hình học.
Phương pháp giải:
Vẽ các dáng đồ thị thỏa mãn bài toán và nhận xét.
Hướng dẫn giải:
Nếu hàm số y = f(x) không liên tục trên đoạn [a; b] nhưng \(f\left( a \right)f\left( b \right) < 0\) thì phương trình \(f\left( x \right) = 0\) có thể có nghiệm hoặc vô nghiệm trong khoảng (a; b)
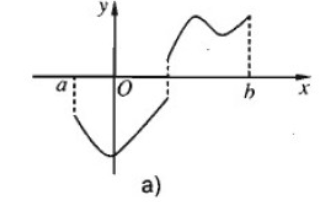
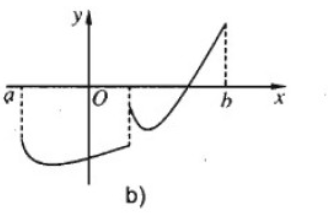
13. Giải bài 4.44 trang 172 SBT Đại số & Giải tích 11
Cho hàm số f(x) xác định trên khoảng K chứa a. Hàm số f(x) liên tục tại x = a nếu:
A. f(x) có giới hạn hữu hạn khi x → a
B. \(\mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {a^ - }} f\left( x \right) = + \infty\)
C. \(\mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {a^ - }} f\left( x \right) = a\)
D. \(\mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {a^ - }} f\left( x \right) = f\left( a \right)\)
Phương pháp giải:
Hàm số y = f(x) liên tục tại \({x_0} \Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Hướng dẫn giải:
Hàm số f(x) liên tục tại x = a nếu \(\mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {a^ - }} f\left( x \right) = f\left( a \right) .\)
Chọn đáp án D.
14. Giải bài 4.45 trang 172 SBT Đại số & Giải tích 11
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{{x^2} + 3x + 2}}{{{x^2} + x}}\, \ nếu\,x \ne - 1\\3x + a\, \ nếu\,x = - 1\end{array} \right.\)
Với giá trị nào của tham số a thì hàm số f(x) liên tục tại x = -1?
A. a = 2 B. a = 4
C. a = 3 D. a = 6
Phương pháp giải:
- Tính f(-1)
- Tính \(\mathop {\lim }\limits_{x \to - 1} f\left( x \right)\)
- Giải phương trình \(\mathop {\lim }\limits_{x \to - 1} f\left( x \right)=f(-1)\) để tìm a.
Hướng dẫn giải:
Ta có: \(f\left( { - 1} \right) = 3.\left( { - 1} \right) + a = a - 3\)
\( \begin{array}{l}\mathop {\lim }\limits_{x \to - 1} f\left( x \right) = \mathop {\lim }\limits_{x \to - 1} \dfrac{{{x^2} + 3x + 2}}{{{x^2} + x}}\\ = \mathop {\lim }\limits_{x \to - 1} \dfrac{{\left( {x + 1} \right)\left( {x + 2} \right)}}{{x\left( {x + 1} \right)}}\\ = \mathop {\lim }\limits_{x \to - 1} \dfrac{{x + 2}}{x}\\ = \dfrac{{ - 1 + 2}}{{ - 1}}\\ = - 1\end{array}\)
Hàm số liên tục tại \(x = - 1 \)
\(\Leftrightarrow \mathop {\lim }\limits_{x \to - 1} f\left( x \right) = f\left( { - 1} \right) \Leftrightarrow - 1 = a - 3 \Leftrightarrow a = 2 .\)
Chọn đáp án: A.
15. Giải bài 4.46 trang 172 SBT Đại số & Giải tích 11
Phương trình x4 - 3x2 + 1 = 0
A. Không có nghiệm trong (-1; 3)
B. Không có nghiệm trong (0; 1)
C. Có ít nhất hai nghiệm
D. Chỉ có một nghiệm duy nhất
Phương pháp giải:
Tính f(0), f(1), f(3) và nhận xét về dấu của chúng để kết luận.
Hướng dẫn giải:
Xét hàm \(f\left( x \right) = {x^4} - 3{x^2} + 1\) trên \(\left( {0;1} \right),\left( {1;3} \right)\) ta có:
Hàm số liên tục trên R nên liên tục trên các khoảng đó.
\( f\left( 0 \right) = 1 > 0 \\ f\left( 1 \right) = - 1 < 0 \\ f\left( 3 \right) = 55 > 0\)
Do đó \(f\left( 0 \right).f\left( 1 \right) < 0\) nên phương trình \(f\left( x \right) = 0\) có ít nhất một nghiệm thuộc \(\left( {0;1} \right)\)
⇒ A, B sai.
Lại có \(f\left( 1 \right).f\left( 3 \right) < 0\) nên phương trình \(f\left( x \right) = 0\) có ít nhất một nghiệm thuộc \(\left( {1;3} \right)\)
⇒ Phương trình \(f\left( x \right) = 0\) có ít nhất hai nghiệm.
Chọn đáp án: C
