Giải bài tập SBT Toán 11 Bài 4: Hai mặt phẳng vuông góc
Dưới đây là hướng dẫn giải bài tập SBT Toán 11 Bài Hai mặt phẳng vuông góc trang 150-152 với nội dung gồm 11 bài tập có hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. eLib hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 11 học tập thật tốt.
Mục lục nội dung
1. Giải bài 3.22 trang 150 SBT Hình học 11
2. Giải bài 3.23 trang 150 SBT Hình học 11
3. Giải bài 3.24 trang 150 SBT Hình học 11
4. Giải bài 3.25 trang 150 SBT Hình học 11
5. Giải bài 3.26 trang 151 SBT Hình học 11
6. Giải bài 3.27 trang 151 SBT Hình học 11
7. Giải bài 3.28 trang 151 SBT Hình học 11
8. Giải bài 3.29 trang 151 SBT Hình học 11
9. Giải bài 3.30 trang 151 SBT Hình học 11

1. Giải bài 3.22 trang 150 SBT Hình học 11
Hình hộp ABCD.A’B’C’D’ có tất cả các cạnh đều bằng nhau. Chứng minh rằng \(AC \bot B'D',AB' \bot C{\rm{D}}'\) và \(A{\rm{D}}' \bot CB'\). Khi nào mặt phẳng (AA’C’C) vuông góc với mặt phẳng (BB’D’D)?
Phương pháp giải:
- Dựa vào tính chất hai đường chéo vuông góc của hình thoi để chứng minh các cặp đường thẳng song song.
Hướng dẫn giải:
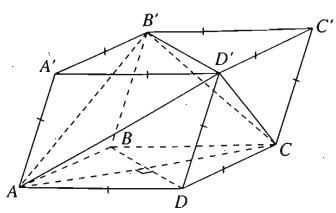
Theo giả thiết các mặt của hình hộp đều là hình thoi.
Ta có ABCD là hình thoi nên \(AC \bot B{\rm{D}}\)
Theo tính chất của hình hộp: BD // B'D' ,do đó \(AC \bot B'{\rm{D'}}\).
Chứng minh tương tự ta được \(AB' \bot C{\rm{D', AD}}' \bot CB'\)
Hai mặt phẳng (AA’C’C) và (BB’D’D) vuông góc với nhau khi hình hộp ABCD.A’B’C’D’là hình lập phương.
2. Giải bài 3.23 trang 150 SBT Hình học 11
Cho tứ diện ABCD có ba cặp cạnh đối diện bằng nhau là AB = CD, AC = BD và AD = BC. Gọi M và N lần lượt là trung điểm của AB và CD. Chứng minh \(MN \bot AB\) và \(MN \bot C{\rm{D}}\). Mặt phẳng (CDM) có vuông góc với mặt phẳng (ABN) không? Vì sao?
Phương pháp giải:
Sử dụng tam giác bằng nhau, tính chất tam giác cân để chứng minh đường thẳng MN vuông góc với hai đường thẳng AB, CD.
Hướng dẫn giải:
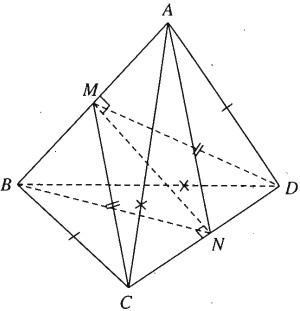
Hai tam giác ABC và BAD bằng nhau ( c.c.c) nên có các đường trung tuyến tương ứng bằng nhau: CM = DM
Ta có tam giác MCD cân tại M, do đó \(MN \bot C{\rm{D}}\) vì N là trung điểm của CD.
Tương tự ta chứng minh được NA = NB và suy ra \(MN \bot AB\).
Mặt phẳng (CDM) không vuông góc với mặt phẳng (ABN) vì (CDM) chứa MN vuông góc với chỉ một đường thẳng AB thuộc (ABN) mà thôi.
3. Giải bài 3.24 trang 150 SBT Hình học 11
Chứng minh rằng nếu tứ diện ABCD có \(AB \bot C{\rm{D}}\) và \(AC \bot B{\rm{D}}\) thì \(AD \bot BC\).
Phương pháp giải:
Vẽ \(AH \bot \left( {BC{\rm{D}}} \right)\), chứng minh H là trực tâm của tam giác BCD.
→ \(AD \bot BC\).
Hướng dẫn giải:
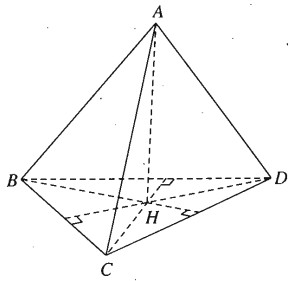
Vẽ \(AH \bot \left( {BC{\rm{D}}} \right)\) tại H, ta có \(C{\rm{D}} \bot AH\) và vì \(C{\rm{D}} \bot AB\) ta suy ra \(C{\rm{D}} \bot BH\).
Tương tự vì \({\rm{BD}} \bot AC\) ta suy ra \({\rm{BD}} \bot CH\)
Vậy H là trực tâm của tam giác BCD tức là \(DH \bot BC\)
Vì \(AH \bot BC\) nên ta suy ra \(BC \bot A{\rm{D}}\)
4. Giải bài 3.25 trang 150 SBT Hình học 11
Cho tam giác ABC vuông tại B. Một đoạn thẳng AD vuông góc với mặt phẳng (ABC). Chứng minh rằng mặt phẳng (ABD) vuông góc với mặt phẳng (BCD).
Từ điểm A trong mặt phẳng (ABD) ta vẽ AH vuông góc với BD, chứng minh rằng AH vuông góc với mặt phẳng (BCD).
Phương pháp giải:
- Chứng minh (BCD) chứa đường thẳng vuông góc với mặt phẳng (ABD).
- Chứng minh AH vuông góc với BD → AH vuông góc với mặt phẳng (BCD).
Hướng dẫn giải:
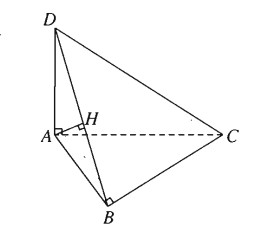
Vì \(A{\rm{D}} \bot \left( {ABC} \right)\) nên \(A{\rm{D}} \bot BC\)
Ngoài ra \(BC \bot AB\) nên ta có \(BC \bot \left( {ABD} \right)\)
Vì mặt phẳng (BCD) chứa BC mà \(BC \bot \left( {ABD} \right)\) nên ta suy ra mặt phẳng (BCD) vuông góc với mặt phẳng (ABD).
Hai mặt phẳng (BCD) và (ABD) vuông góc với nhau và có giao tuyến là BD.
Đường thẳng AH thuộc mặt phẳng (ABD) và vuông góc với giao tuyến BD nên AH vuông góc với mặt phẳng (BCD).
5. Giải bài 3.26 trang 151 SBT Hình học 11
Hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a và có SA = SB = SC = a. Chứng minh:
a) Mặt phẳng (ABCD) vuông góc với mặt phẳng (SBD)
b) Tam giác SBD là tam giác vuông tại S.
Phương pháp giải:
a) (ABCD) chứa đường thẳng vuông góc với mặt phẳng (SBD).
b) Chứng minh tam giác SBD có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó.
Hướng dẫn giải:
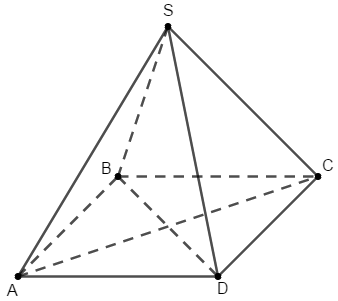
a) Gọi O là tâm của hình thoi, ta có \(AC \bot BD\) tại O
Vì SA = SC nên \(SO \bot AC.\)
Do đó AC vuông góc với mặt phẳng (SBD)
Ta suy ra mặt phẳng (ABCD) vuông góc với mặt phẳng (SBD).
b) Ba tam giác SAC, BAC, DAC bằng nhau ( c.c.c) nên ta suy ra OS = OB = OD.
Vậy tam giác SBD vuông tại S.
6. Giải bài 3.27 trang 151 SBT Hình học 11
a) Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Chứng minh rằng đường thẳng AC’ vuông góc với mặt phẳng (A’BD) và mặt phẳng (ACC’A’) vuông góc với mặt phẳng (A’BD).
b) Tính đường chéo AC’ của hình lập phương đã cho.
Phương pháp giải:
a) Chứng minh A và C’ thuộc trục đường tròn ngoại tiếp tam giác BDA’.
b) Áp dụng định lý Pytago vào tam giác ACC'.
Hướng dẫn giải:
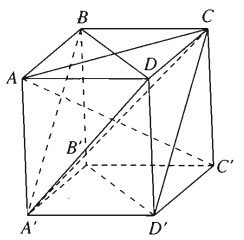
a) Ta có AB = AD = AA' = a và C'B = C'D = C'A' = \(a\sqrt 2\)
Vì hai điểm A và C’ cách đều ba đỉnh của tam giác A’BD nên A và C’ thuộc trục đường tròn ngoại tiếp tam giác BDA’.
Vậy \(AC' \bot \left( {B{\rm{D}}A'} \right).\)
Mặt khác vì mặt phẳng (ACC’A’) chứa đường thẳng AC’ mà \(AC' \bot \left( {B{\rm{D}}A'} \right)\) nên ta suy ra mặt phẳng (ACC’A’) vuông góc với mặt phẳng (BDA’)
b) Ta có ACC’ là tam giác vuông có cạnh \(AC = a\sqrt 2 \) và CC’ = a
Vậy \(AC{'^2} = A{C^2} + CC{'^2} \Rightarrow AC{'^2} = 2{{\rm{a}}^2} + {a^2} = 3{{\rm{a}}^2}\)
Vậy \(AC' = a\sqrt 3.\)
7. Giải bài 3.28 trang 151 SBT Hình học 11
Cho hình chóp đều S.ABC. Chứng minh:
a) Mỗi cạnh bên của hình chóp đó vuông góc với cạnh đối diện;
b) Mỗi mặt phẳng chứa một cạnh bên và đường cao của hình chóp đều vuông góc với cạnh đối diện.
Phương pháp giải:
a) Dùng định lí ba đường vuông góc để chứng minh.
b) Chứng minh đường thẳng vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.
Hướng dẫn giải:
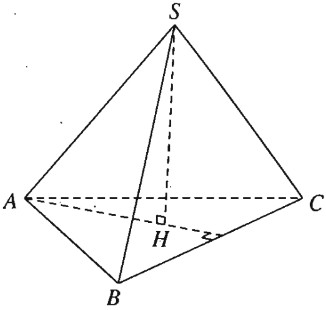
a) Vì S.ABC là hình chóp đều nên ∆ABC là tam giác đều và có SA = SB = SC.
Do đó khi ta vẽ \(SH \bot \left( {ABC} \right)\) thì H là trọng tâm của tam giác đều ABC và ta có \(AH \bot BC\).
Theo định lí ba đường vuông góc ta có \(SA \bot BC\).
Chứng minh tương tự ta có \(SB \bot AC\) và \(SC \bot AB\)
b) Vì \(BC \bot AH\) và \(BC \bot SH\) nên \(BC \bot \left( {SAH} \right)\)
Chứng minh tương tự ta có \(CA \bot \left( {SBH} \right)\) và \(AB \bot \left( {SCH} \right).\)
8. Giải bài 3.29 trang 151 SBT Hình học 11
Tứ diện SABC có SA vuông góc với mặt phẳng (ABC). Gọi H và K lần lượt là trực tâm của các tam giác ABC và SBC. Chứng minh rằng:
a) AH, SK và BC đồng quy.
b) SC vuông góc với mặt phẳng (BHK) và \(\left( {SAC} \right) \bot \left( {BHK} \right)\)
c) HK vuông góc với mặt phẳng (SBC) và \(\left( {SBC} \right) \bot \left( {BHK} \right)\)
Phương pháp giải:
a) Gọi A’ là giao điểm của AH và BC. Chứng minh ba điểm S, K, A’ thẳng hàng.
b) Chứng minh SC vuông góc với hai đường thẳng cắt nhau thuộc (BHK) → \(\left( {SAC} \right) \bot \left( {BHK} \right)\).
c) Chứng minh HK vuông góc với hai đường thẳng cắt nhau thuộc (SBC) → \(\left( {SBC} \right) \bot \left( {BHK} \right)\)
Hướng dẫn giải:
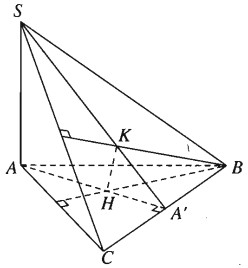
a) Vì H là trực tâm của tam giác ABC nên
Mặt khác theo giả thiết ta có: \(SA \bot \left( {ABC} \right)\), do đó \(SA \bot BC\).
Từ đó ta suy ra \(BC \bot \left( {SAA'} \right)\) và \(BC \bot SA'\).
⇒ SA’ là đường cao của tam giác SBC nên SA’ là phải đi qua trực tâm K.
Vậy ba đường thẳng AH, SK và BC đồng quy.
b) Vì K là trực tâm của tam giác SBC nên \(BK \bot SC\left( 1 \right)\)
Mặt khác ta có \(BH \bot AC\) vì H là trực tâm của tam giác ABC và \(BH \bot SA\) vì \(SA \bot \left( {ABC} \right).\)
Do đó \(BH \bot \left( {ABC} \right)\) nên \(BH \bot SC\left( 2 \right).\)
Từ (1) và (2) ta suy ra \(SC \bot \left( {BHK} \right)\).
Vì mặt phẳng (SAC) chứa SC mà \(SC \bot \left( {BHK} \right)\) nên ta có \(\left( {SAC} \right) \bot \left( {BHK} \right).\)
c) Ta có:
\( \left. \matrix{ BC \bot \left( {SAA'} \right),BC \bot HK \hfill \cr SC \bot \left( {BHK} \right),SC \bot HK \hfill \cr} \right\} \Rightarrow HK \bot \left( {SBC} \right)\)
Mặt phẳng (BHK) chứa HK mà \(HK \bot \left( {SBC} \right)\) nên \(\left( {BHK} \right) \bot \left( {SBC} \right).\)
9. Giải bài 3.30 trang 151 SBT Hình học 11
Tứ diện SABC có ba đỉnh A, B, C tạo thành tam giác vuông cân đỉnh B và, có cạnh SA vuông góc với mặt phẳng (ABC) và SA = a.
a) Chứng minh mặt phẳng (SAB) vuông góc với mặt phẳng (SBC).
b) Trong mặt phẳng (SAB) vẽ AH vuông góc với SB tại H, chứng minh \(AH \bot \left( {SBC} \right)\)
c) Tính độ dài đoạn AH.
d) Từ trung điểm O của đoạn AC vẽ OK vuông góc với (SBC) cắt (SBC) tại K. Tính độ dài đoạn OK.
Phương pháp giải:
a) Chứng minh (SBC) chứa hai đường thẳng cắt nhau vuông góc với (SAB).
b) Chứng minh AH vuông góc với đường thẳng thuộc (SBC).
c) Áp dụng hệ thức lượng trong tam giác vuông SAB.
d) Chứng minh OK là đường trung bình của tam giác AHC.
Hướng dẫn giải:
.jpg)
a) Ta có:
\( \displaystyle \left. \matrix{ BC \bot AB \hfill \cr BC \bot SA \hfill \cr} \right\} \Rightarrow BC \bot \left( {SAB} \right) \displaystyle \Rightarrow \left( {SBC} \right) \bot \left( {SAB} \right)\)
b) \(\displaystyle AH \bot SB\) mà SB giao tuyến của hai mặt phẳng vuông góc là (SBC) và (SAB) nên \(\displaystyle AH \bot \left( {SBC} \right).\)
c) Xét tam giác vuông SAB với đường cao AH ta có:
\( \displaystyle {1 \over {A{H^2}}} = {1 \over {A{S^2}}} + {1 \over {A{B^2}}} \displaystyle = {1 \over {{a^2}}} + {1 \over {2{a^2}}} = {3 \over {2{a^2}}}\)
Vậy \(\displaystyle AH = {{a\sqrt 6 } \over 3}\)
d) Vì \(\displaystyle OK \bot \left( {SBC} \right)\) mà \(\displaystyle AH \bot \left( {SBC} \right)\) nên \(\displaystyle OK\parallel AH\), ta có K thuộc CH.
\(\displaystyle OK = {{AH} \over 2} = {{a\sqrt 6 } \over 6} \)
10. Giải bài 3.31 trang 151 SBT Hình học 11
Hình chóp S.ABCD có đáy là hình vuông ABCD tâm O và có cạnh SA vuông góc với mặt phẳng (ABCD). Giả sử \(\left( \alpha \right)\) là mặt phẳng đi qua A và vuông góc với cạnh SC, \(\left( \alpha \right)\) cắt SC tại I.
a) Xác định giao điểm K của SO với mặt phẳng \(\left( \alpha \right).\)
b) Chứng minh mặt phẳng (SBD) vuông góc với mặt phẳng (SAC) và \(BD//\left( \alpha \right)\)
c) Xác định giao tuyến d của mặt phẳng (SBD) và mặt phẳng \(\left( \alpha \right)\). Tìm thiết diện cắt hình chóp S.ABCD bởi mặt phẳng \(\left( \alpha \right)\)
Phương pháp giải:
a) Gọi \(I=SC \cap(\alpha)\) → K là giao điểm của AI và SO
b) Chứng minh (SBD) chứa hai đường thẳng vuông góc với mặt phẳng (SAC).
c) - Giao tuyến d của mặt phẳng (SBD) và mặt phẳng \((\alpha)\) song song với BD và qua K.
- Thiết diện cần tìm là hình tạo bởi các giao tuyến của \((\alpha)\) với các mặt của hình chóp.
Hướng dẫn giải:
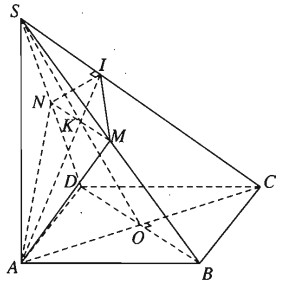
a) Gọi I là giao điểm của mặt phẳng \(\left( \alpha \right)\) với cạnh SC.
Ta có \(\left( \alpha \right) \bot SC\), \(AI \subset \left( \alpha \right) \Rightarrow SC \bot AI\).
Vậy AI là đường cao của tam giác vuông SAC.
Trong mặt phẳng (SAC), đường cao AI cắt SO tại K và \(AI \subset \left( \alpha \right)\), nên K là giao điểm của SO với \(\left( \alpha \right)\).
b) Ta có
\( \left. \matrix{ B{\rm{D}} \bot AC \hfill \cr B{\rm{D}} \bot SA \hfill \cr} \right\} \Rightarrow B{\rm{D}} \bot \left( {SAC} \right) \Rightarrow B{\rm{D}} \bot SC\)
Mặt khác \(B{\rm{D}} \subset \left( {SB{\rm{D}}} \right)\) nên \(\left( {SB{\rm{D}}} \right) \bot \left( {SAC} \right).\)
Vì \(B{\rm{D}} \bot SC\) và \(\left( \alpha \right) \bot SC\) nhưng BD không chứa trong \(\left( \alpha \right)\) nên \(BD//\left( \alpha \right)\)
c) Ta có \( K = SO \cap \left( \alpha \right)\) và SO thuộc mặt phẳng (SBD) nên K là một điểm chung của \(\left( \alpha \right)\) và (SBD).
Mặt phẳng (SBD) chứa \(BD//\left( \alpha \right)\) nên cắt theo giao tuyến d // BD.
Giao tuyến này đi qua K là điểm chung của \(\left( \alpha \right)\) và (SBD).
Gọi M và N lần lượt là giao điểm của d với SB và SD.
Ta được thiết diện là tứ giác AIMN vuông góc với SC và đường chéo MN song song với BD.
11. Giải bài 3.32 trang 152 SBT Hình học 11
Hình chóp S.ABCD có đáy là hình thang svuông ABCD vuông tại A và D, có AB = 2a, AD = DC = a, có cạnh SA vuông góc với mặt phẳng (ABCD) và SA = a.
a) Chứng minh mặt phẳng (SAD) vuông góc với mặt phẳng (SDC), mặt phẳng (SAC) vuông góc với mặt phẳng (SCB).
b) Gọi \(\varphi \) là góc giữa hai mặt phẳng (SBC) và (ABCD), tính \(\tan \varphi.\)
c) Gọi \(\left( \alpha \right)\) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC). Hãy xác định \(\left( \alpha \right)\) và xác định thiết diện của hình chóp S.ABCD với \(\left( \alpha \right)\).
Phương pháp giải:
a) Chứng minh mặt phẳng này chứa hai đường thẳng cắt nhau thuộc mặt phẳng kia.
b) \( \varphi = \widehat {SCA}\) → Tính \(\tan \varphi \)
c) Thiết diện cần tìm là hình tạo bởi các giao tuyến của \((\alpha)\) với các mặt của hình chóp.
Hướng dẫn giải:
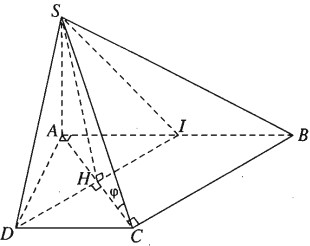
a) Ta có:
\( \left. \matrix{ C{\rm{D}} \bot A{\rm{D}} \hfill \cr C{\rm{D}} \bot SA \hfill \cr} \right\} \Rightarrow C{\rm{D}} \bot \left( {SA{\rm{D}}} \right) \Rightarrow \left( {SC{\rm{D}}} \right) \bot \left( {SA{\rm{D}}} \right)\)
Gọi I là trung điểm của đoạn AB.
Ta có AICD là hình vuông và IBCD là hình bình hành.
Vì DI // CB và \(DI \bot CA\) nên \(AC \bot CB\). Do đó \(CB \bot \left( {SAC} \right).\)
Vậy \(\left( {SBC} \right) \bot \left( {SAC} \right).\)
b) Ta có:
\( \varphi = \widehat {SCA} \Rightarrow \tan \varphi = {{SA} \over {AC}} = {a \over {a\sqrt 2 }} = {{\sqrt 2 } \over 2}\)
c) Ta có:
\( \left. \matrix{ DI \bot AC \hfill \cr DI \bot SA \hfill \cr} \right\} \Rightarrow DI \bot \left( {SAC} \right)\)
Vậy \(\left( \alpha \right)\) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC) chính là mặt phẳng (SDI).
Do đó thiết diện của \(\left( \alpha \right)\) với hình chóp S.ABCD là tam giác đều SDI có chiều dài mỗi cạnh bằng \(a\sqrt 2. \)
Gọi H là tâm hình vuông AICD ta có \(SH \bot DI\) và \(SH = {{DI\sqrt 3 } \over 2} = {{a\sqrt 6 } \over 2}. \)
Tam giác SDI có diện tích:
\(S_{ \Delta S{\rm{D}}I} = {1 \over 2}SH.DI = {1 \over 2}{{a\sqrt 6 } \over 2}.a\sqrt 2 = {{{a^2}\sqrt 3 } \over 2} \)
Tham khảo thêm
- doc Giải bài tập SBT Toán 11 Bài 1: Vectơ trong không gian
- doc Giải bài tập SBT Toán 11 Bài 2: Hai đường thẳng vuông góc
- doc Giải bài tập SBT Toán 11 Bài 3: Đường thẳng vuông góc với mặt phẳng
- doc Giải bài tập SBT Toán 11 Bài 5: Khoảng cách
- doc Giải bài tập SBT Hình học 11 Ôn tập chương 3: Vectơ trong không gian. Quan hệ vuông góc trong không gian
