Giải bài tập SBT Toán 11 Bài 3: Đường thẳng vuông góc với mặt phẳng

Một đoạn thẳng AB không vuông góc với mặt phẳng \(\left( \alpha \right)\) cắt mặt phẳng này tại trung điểm O của đoạn thẳng đó. Các đường thẳng vuông góc với \(\left( \alpha \right)\) qua A và B lần lượt cắt mặt phẳng \(\left( \alpha \right)\) tại A’ và B’. Chứng minh ba điểm A’, O, B’ thẳng hàng và AA’ = BB’.

Phương pháp giải:

- Chứng minh ba điểm O, A', B' cùng thuộc giao tuyến của (AA’, BB’) với \(\left( \alpha \right)\).

- Chứng minh hai tam giác bằng nhau theo trường hợp cạnh huyền góc nhọn.

Hướng dẫn giải:

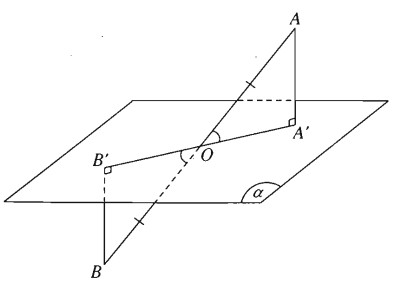
\( \left\{ \matrix{ AA' \bot \left( \alpha \right) \hfill \cr BB' \bot \left( \alpha \right) \hfill \cr} \right. \Rightarrow AA'\parallel BB'\)

Mặt phẳng (AA’, BB’)  xác định bởi hai đường thẳng song song (AA’, BB’)  cắt mặt phẳng \(\left( \alpha \right)\) theo giao tuyến qua O, A’, B’.

Do đó ba điểm O, A’, B’  thẳng hàng.

Hai tam giác vuông OAA’  và OBB’  bằng nhau vì có một cạnh huyền và một góc nhọn bằng nhau nên từ đó ta suy ra AA’ = BB’.

Cho tam giác ABC. Gọi \(\left( \alpha \right)\) là mặt phẳng vuông góc với đường thẳng CA tại A và \(\left( \beta \right)\) là mặt phẳng vuông góc với đường thẳng CB tại B. Chứng minh rằng hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) cắt nhau và giao tuyến d của chúng vuông góc với mặt phẳng (ABC).

Phương pháp giải:

Biện luận từng trường hợp để chứng minh \((\alpha)\) cắt \((\beta)\).

Hướng dẫn giải:

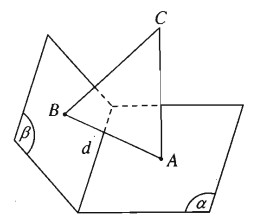
Hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) không thể trùng nhau vì nếu chúng trùng nhau thì từ một điểm C ta dựng được hai đường thẳng CA, CB cùng vuông góc với một mặt phẳng (vô lí).

Mặt khác \(\left( \alpha \right)\) và \(\left( \beta \right)\) cũng không song song với nhau.

Vì nếu \(\left( \alpha \right) // \left( \beta \right)\), thì từ \(CB \bot \left( \beta \right)\) ta suy ra \(CB \bot \left( \alpha \right)\)

Như vậy từ một điểm C ta dựng được hai đường thẳng CA, CB cùng vuông góc với \(\left( \alpha \right)\) (vô lí).

Vậy \(\left( \alpha \right)\) và \(\left( \beta \right)\) là hai mặt phẳng không trùng nhau, không song song với nhau và chúng phải cắt nhau theo giao tuyến d, nghĩa là \(d = \left( \alpha \right) \cap \left( \beta \right)\)

\( \eqalign{ & \left\{ \matrix{ d \subset \left( \alpha \right) \hfill \cr CA \bot \left( \alpha \right) \hfill \cr} \right. \Rightarrow CA \bot d\,\,\,\,\,\,\left( 1 \right) \cr & \left\{ \matrix{ d \subset \left( \beta \right) \hfill \cr CB \bot \left( \beta \right) \hfill \cr} \right. \Rightarrow CB \bot d\,\,\,\,\,\left( 2 \right) \cr}\)

Từ (1) và (2) suy ra \(d \bot \left( {ABC} \right).\)

Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi H là trực tâm của tam giác ABC và biết rằng A’H vuông góc với mặt phẳng (ABC). Chứng minh rằng:

a) AA' ⊥ BC và AA’ ⊥ B’C’.

b) Gọi MM’ là giao tuyến của mặt phẳng (AHA’) với mặt bên BCC’B’, trong đó M ∈ BC và M’ ∈ B’C’. Chứng minh rằng tứ giác BCC’B là hình chữ nhật và MM’ là đường cao của hình chữ nhật đó.

Phương pháp giải:

a) - Chứng minh BC vuông góc với mặt phẳng chứa AA'.

- Chứng minh AA' vuông góc với một đường thẳng song song B'C'.

b) - Chứng minh BCC'B là hình bình hành có 1 góc vuông.

- Chứng minh MM' \(\bot\) BC và MM' \(\bot\) B'C'.

Hướng dẫn giải:

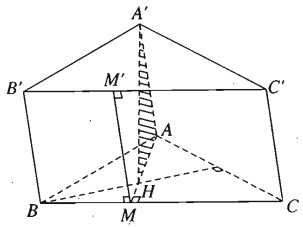
a) Ta có:

\(BC \bot AH,BC \bot A'H \\ \Rightarrow BC \bot \left( {A'HA} \right) \Rightarrow BC \bot AA'\)

Và \(B'C' \bot AA' \) vì BC // B'C'.

b) Ta có AA' // BB' // CC' mà BC \(\bot\) AA' nên tứ giác BCC’B’ là hình chữ nhật.

Vì AA' // (BCC'B') nên ta suy ra MM' \(\bot\) BC và MM' \(\bot\) B'C' hay MM’ là đường cao của hình chữ nhật BCC’B’.

Hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại A và có cạnh bên SA vuông góc với mặt phẳng đáy là (ABC). Gọi D là điểm đối xứng của của điểm B qua trung điểm O của cạnh AC. Chứng minh rằng \(C{\rm{D}} \bot CA\) và \(C{\rm{D}} \bot \left( {SCA} \right).\)

Phương pháp giải:

- Chứng minh CA vuông góc với đường thẳng song song với CD.

- Chứng minh CD vuông góc với hai đường thẳng cắt nhau thuộc (SCA).

Hướng dẫn giải:

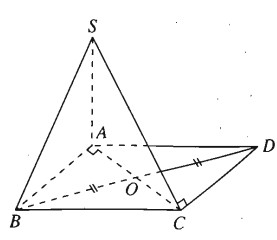
Ta có

\( SA \bot \left( {ABC} \right) \Rightarrow SA \bot DC \subset \left( {ABC} \right)\)

Vì AC và BD cắt nhau tại trung điểm O của mỗi đoạn nên tứ giác ABCD là hình bình hành và ta có AB // CD.

Vì AB \(\bot\) AC nên \(C{\rm{D}} \bot CA.\)

Mặt khác ta có \(C{\rm{D}} \bot SA\), do đó \(C{\rm{D}} \bot \left( {SCA} \right).\)

Hai tam giác cân ABC và DBC nằm trong hai mặt phẳng khác nhau có chung cạnh đáy BC tạo nên tứ diện ABCD. Gọi I là trung điểm của cạnh BC.

a) Chứng minh \(BC \bot A{\rm{D}}\)

b) Gọi AH là đường cao của tam giác ADI

Chứng minh rằng AH vuông góc với mặt phẳng (BCD).

Phương pháp giải:

a) Chứng minh BC vuông góc với mặt phẳng chứa SD.

b) Chứng minh AH vuông góc với hai đường thẳng cắt nhau thuộc (BCD).

Hướng dẫn giải:

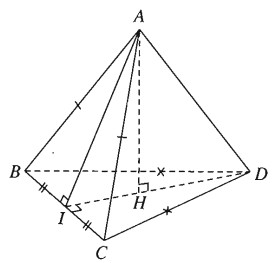
a) Tam giác ABC cân đỉnh A và có I là trung điểm của BC nên AI \(\bot\) BC.

Tương tự tam giác DBC cân đỉnh D và có có I là trung điểm của BC nên DI \(\bot\) BC. Ta suy ra:

\( BC \bot \left( {AI{\rm{D}}} \right) \) nên \(BC \bot A{\rm{D}}.\)

b) Vì \(BC \bot \left( {AI{\rm{D}}} \right)\) nên \(BC \bot AH\)

Mặt khác \(AH \bot I{\rm{D}}\) nên ta suy ra AH vuông góc với mặt phẳng (BCD).

Chứng minh rằng tập hợp những điểm cách đều ba đỉnh của tam giác ABC là đường thẳng d vuông góc với mặt phẳng (ABC) tại tâm O của đường tròn (C) ngoại tiếp tam giác ABC đó.

Phương pháp giải:

Chứng minh hai chiều:

- Giả sử M cách đều A,B,C suy ra M nằm trên đường thẳng vuông góc với (ABC) tại tâm đường tròn ngoại tiếp tam giác ABC.

- Giả sử M thuộc đường thẳng vuông góc với (ABC) tại tâm đường tròn ngoại tiếp tam giác ABC và chứng minh M cách đều A,B,C.

Hướng dẫn giải:

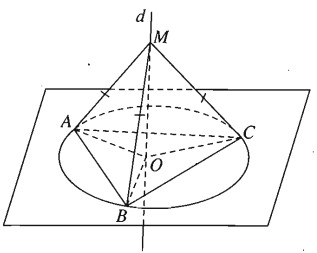
- Phần thuận

Nếu MA = MB = MC nghĩa là M cách đều ba đỉnh của tam giác ABC và MO vuông góc với mặt phẳng (ABC) thì ta có ba tam giác vuông MOA, MOB, MOC bằng nhau.

Từ đó ta suy ra OA = OB = OC nghĩa là A, B, C nằm trên đường tròn tâm O ngoại tiếp tam giác ABC.

Vậy điểm M cách đều ba đỉnh của tam giác ABC thì nằm trên đường thẳng d vuông góc với mặt phẳng (ABC) tại tâm O của đường tròn ngoại tiếp tam giác ABC.

- Phần đảo

Nếu ta lấy một điểm M bất kì thuộc đường thẳng d nói trên thì ta có ba tam giác vuông MOA, MOB, MOC bằng nhau.

Do đó ta suy ra MA = MB = MC nghĩa là điểm M cách đều ba đỉnh của tam giác ABC.

Kết luận. Tập hợp những điểm cách đều ba đỉnh của tam giác ABC là đường thẳng d vuông góc với mặt phẳng (ABC) tại tâm O của đường tròn (C) ngoại tiếp tam giác ABC đó.