Giải bài tập SBT Hình học 11 Ôn tập chương 3: Vectơ trong không gian. Quan hệ vuông góc trong không gian
Gửi đến các em nội dung giải bài tập SBT Ôn tập chương 3: Vectơ trong không gian. Quan hệ vuông góc trong không gian môn Hình học 11 được eLib biên soạn và tổng hợp bên dưới đây. Tài liệu gồm các câu hỏi theo chuẩn kiến thức, kĩ năng có đáp án và phương pháp giải chi tiết để các em tham khảo. Tài liệu giúp các em kiểm tra năng lực của bản thân cũng như đúc rút thêm kinh nghiệm làm bài. Cùng cố gắng để đạt kết quả cao nhé!. Chúc các em thành công.
Mục lục nội dung
1.1. Giải bài 3.41 trang 161 SBT Hình học 11
1.2. Giải bài 3.42 trang 161 SBT Hình học 11
1.3. Giải bài 3.43 trang 161 SBT Hình học 11
1.4. Giải bài 3.44 trang 162 SBT Hình học 11
1.5. Giải bài 3.45 trang 162 SBT Hình học 11
1.6. Giải bài 3.45 trang 162 SBT Hình học 11
1.7. Giải bài 3.47 trang 162 SBT Hình học 11
1.8. Giải bài 3.48 trang 162 SBT Hình học 11
2.1. Giải bài 3.49 trang 163 SBT Hình học 11
2.2. Giải bài 3.50 trang 163 SBT Hình học 11
2.3. Giải bài 3.51 trang 163 SBT Hình học 11
2.4. Giải bài 3.52 trang 163 SBT Hình học 11
2.5. Giải bài 3.53 trang 163 SBT Hình học 11
3.1. Giải bài 3.54 trang 164 SBT Hình học 11
3.2. Giải bài 3.55 trang 164 SBT Hình học 11
3.3. Giải bài 3.56 trang 164 SBT Hình học 11
3.4. Giải bài 3.57 trang 164 SBT Hình học 11
3.5. Giải bài 3.58 trang 164 SBT Hình học 11
3.6. Giải bài 3.59 trang 164 SBT Hình học 11
3.7. Giải bài 3.60 trang 165 SBT Hình học 11
3.8. Giải bài 3.61 trang 165 SBT Hình học 11
3.9. Giải bài 3.62 trang 165 SBT Hình học 11
3.10. Giải bài 3.63 trang 165 SBT Hình học 11
3.11. Giải bài 3.64 trang 166 SBT Hình học 11
3.12. Giải bài 3.65 trang 166 SBT Hình học 11
3.13. Giải bài 3.66 trang 166 SBT Hình học 11
3.14. Giải bài 3.67 trang 166 SBT Hình học 11
3.15. Giải bài 3.68 trang 167 SBT Hình học 11
3.16. Giải bài 3.69 trang 167 SBT Hình học 11
3.17. Giải bài 3.70 trang 167 SBT Hình học 11
3.18. Giải bài 3.71 trang 167 SBT Hình học 11

1. Câu hỏi và bài tập
1.1. Giải bài 3.41 trang 161 SBT Hình học 11
Trong các mệnh đề sau đây mệnh đề nào đúng? Mệnh đề nào sai?
a) Cho hai đường thẳng a và b song song với nhau. Nếu có một đường thẳng d vuông góc với a thì d vuông góc với b.
b) Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì chúng song song với nhau.
c) Một mặt phẳng \(\left( \alpha \right)\) và một đường thẳng a cùng vuông góc với đường thằng b thì \(a// \left( \alpha \right).\)
d) Hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) phân biệt cùng vuông góc với một mặt phẳng \(\left( \gamma \right)\) thì \(\left( \alpha \right)// \left( \beta \right).\)
e) Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song với nhau.
f) Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song.
Phương pháp giải:
Suy luận từng mệnh đề, cho ví dụ nếu mệnh đề sai.
Hướng dẫn giải:
a) Đúng
b) Đúng
c) Sai vì có thể xảy ra \(a \subset \left( \alpha \right)\)
d) Sai vì có thể xảy ra hai mặt phẳng cắt nhau theo giao tuyến vuông góc với \(\left( \gamma \right)\)
e) Sai vì chúng có thể cắt nhau và cùng nằm trong mặt phẳng chứa hai đường thẳng đó.
f) Đúng.
1.2. Giải bài 3.42 trang 161 SBT Hình học 11
Xét các khẳng định sau đây xem khẳng định nào đúng, khẳng định nào sai?
a) Qua một điểm, có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
b) Qua một đường thẳng, có duy nhất một mặt phẳng vuông góc với một đường thẳng cho trước.
c) Qua một điểm, có duy nhất một mặt phẳng vuông góc với một đường thẳng cho trước.
d) Cho hai đường thẳng a và b. Nếu có mặt phẳng \(\left( \alpha \right)\) không chứa cả a và b thì a và b chéo nhau.
Phương pháp giải:
Suy luận từng mệnh đề, cho ví dụ nếu mệnh đề sai.
Hướng dẫn giải:
a) Sai vì có vô số mặt phẳng thỏa mãn.
b) Sai vì có vô số mặt phẳng thỏa mãn.
c) Đúng.
d) Sai vì a, b vẫn có thể cắt nhau, song song, trùng nhau, chéo nhau mà vẫn có vô số mặt phẳng không chứa cả hai đường thẳng.
1.3. Giải bài 3.43 trang 161 SBT Hình học 11
Trên mặt phẳng \(\left( \alpha \right)\) cho hình vuông ABCD. Các tia Ax, By, Cz, Dt vuông góc với mặt phẳng \(\left( \alpha \right)\) và nằm về một phía đối với mặt phẳng \(\left( \alpha \right)\). Một mặt phẳng \(\left( \beta \right)\) lần lượt cắt Ax, By, Cz, Dt tại A’, B’, C’, D’.
a) Tứ giác A’B’C’D’ là hình gì? Chứng minh rằng: AA' + CC' = BB' + DD'
b) Chứng minh rằng điều kiện để tứ giác A’B’C’D’ là hình thoi là nó có hai đỉnh đối diện cách đều mặt phẳng \(\left( \alpha \right).\)
c) Chứng minh rằng điều kiện để tứ giác A’B’C’D’ là hình chữ nhật là nó có hai đỉnh kề nhau cách đều mặt phẳng \(\left( \alpha \right).\)
Phương pháp giải:
a) - Chứng minh A’B’C’D’ có hai cặp cạnh đối song song.
- Gọi O là tâm của hình vuông ABCD và O’ là tâm của hình bình hành A’B’C’D’.
⇒ Dựa vào tính chất đường trung bình để chứng minh AA' + CC' = BB' + DD'.
b) Muốn hình bình hành A’B’C’D’ là hình thoi ta cần phải có A’C’⊥B’D’.
c) Muốn hình bình hành A’B’C’D’ là hình chữ nhật ta cần có A’B’⊥B’C’.
Hướng dẫn giải:
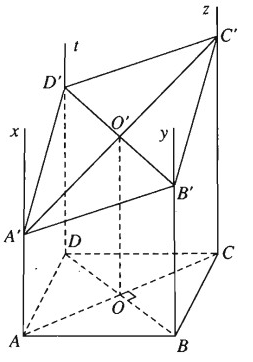
a) Ta có hai mặt phẳng song song là: \( \left( {Ax,AD} \right) // \left( {By,BC} \right)\)
Hai mặt phẳng này bị cắt bởi mặt phẳng \(\left( \beta \right)\) nên ta suy ra các giao tuyến của chúng phải song song nghĩa là A'D' // B'C'.
Tương tự ta chứng minh được A'B' // D'C'.
Vậy A’,B’,C’,D’ là hình bình hành.
Gọi O là tâm của hình vuông ABCD và O’ là tâm của hình bình hành A’B’C’D’
⇒ Các hình thang AA’C’C và BB’D’D đều có OO’ là đường trung bình
⇒ AA' + CC' = BB' + DD' = 2OO'
b) Muốn hình bình hành A’B’C’D’ là hình thoi ta cần phải có A’C’⊥B’D’.
Ta đã có AC⊥BD.
Vậy A’B’C’D’ là hình thoi khi và chỉ khi A’C’ hoặc B’D’ song song với mặt phẳng \(\left( \alpha \right)\) cho trước. Khi đó ta có AA’ = CC’ hoặc BB’ = DD’.
c) Muốn hình bình hành A’B’C’D’ là hình chữ nhật ta cần có A’B’⊥B’C’
⇒ A’B’ hoặc B’C’ phải song song với mặt phẳng \(\left( \alpha \right)\). Khi đó ta có AA’ = BB’ hoặc BB’ = CC’
Nghĩa là hình bình hành A’B’C’D’ có hai đỉnh kề nhau cách đều mặt phẳng \(\left( \alpha \right)\) cho trước.
1.4. Giải bài 3.44 trang 162 SBT Hình học 11
Hình chóp tam giác S.ABC có đáy là tam giác đều ABC cạnh 7a, có cạnh SC vuông góc với mặt phẳng đáy (ABC) và SC = 7a.
a) Tính góc giữa SA và BC.
b) Tính khoảng cách giữa hai đường thẳng chéo nhau SA và BC.
Phương pháp giải:
a) Áp dụng định lí ba đường vuông góc để chứng minh SD⊥DA
⇒ Góc giữa SA và BC là góc SAD.
b) - Chứng minh BC // (SAD).
⇒ d(SA, BC) = d(BC, (SAD)).
- Áp dụng hệ thứ lượng trong tam giác vuông SCD để tính d(SA, BC).
Hướng dẫn giải:
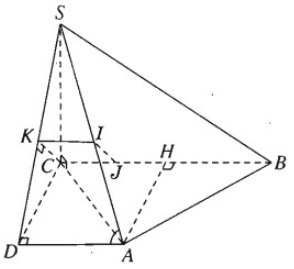
a) Gọi H là trung điểm của đoạn BC.
Qua A vẽ AD song song với BC và bằng đoạn HC thì góc giữa BC và SA là góc SAD.
Theo định lí ba đường vuông góc, ta có SD⊥DA và khi đó:
\( \cos \widehat {SAD} = {{AD} \over {SA}} = {{HC} \over {SA}} = {{{{7a} \over 2}} \over {7a\sqrt 2 }} = {{\sqrt 2 } \over 4}\)
Vậy góc giữa BC và SA được xác định sao cho \(\cos \widehat {SAD} = {{\sqrt 2 } \over 4}\)
b) Vì BC // (lAD) nên BC song song với mặt phẳng (SAD).
Do đó khoảng cách giữa SA và BC chính là khoảng cách từ đường thẳng BC đến mặt phẳng (SAD).
Ta kẻ CK⊥SD, suy ra CK⊥(SAD), do đó CK chính là khoảng cách nói trên.
Xét tam giác vuông SCD với đường cao CK xuất phát từ đỉnh góc vuông C ta có hệ thức:
\( {1 \over {C{K^2}}} = {1 \over {S{C^2}}} + {1 \over {C{D^2}}} \Rightarrow {1 \over {C{K^2}}} = {1 \over {{{\left( {7{\rm{a}}} \right)}^2}}} + {1 \over {{{\left( {{{7{\rm{a}}\sqrt 3 } \over 2}} \right)}^2}}}\)
(vì \(CD = AH = {{BC\sqrt 3 } \over 2} = {{7{\rm{a}}\sqrt 3 } \over 2} \))
Do đó \({1 \over {C{K^2}}} = {1 \over {49{{\rm{a}}^2}}} + {4 \over {3.49{{\rm{a}}^2}}} = {{3 + 4} \over {3.49{{\rm{a}}^2}}} = {1 \over {21{{\rm{a}}^2}}}\)
Vậy \(CK = a\sqrt {21}\)
1.5. Giải bài 3.45 trang 162 SBT Hình học 11
Cho tứ diện ABCD. Chứng minh rằng AB vuông góc với CD khi và chỉ khi \( A{C^2} + B{{\rm{D}}^2} = A{{\rm{D}}^2} + B{C^2}\)
Phương pháp giải:
- Chiều thuận: Áp dụng định lí Py-ta-go cho các tam giác vuông AEC, BEC, AED và BED ⇒ đpcm.
- Chiều nghịch:
+ TH1: \(A{C^2} - A{D^2} = B{C^2} - B{{\rm{D}}^2} = {k^2}\)
+ TH2: \(A{C^2} - A{D^2} = B{C^2} - B{{\rm{D}}^2} = -{k^2}\)
⇒ Chứng minh A, B thuộc đường thẳng vuông góc với CD.
Hướng dẫn giải:
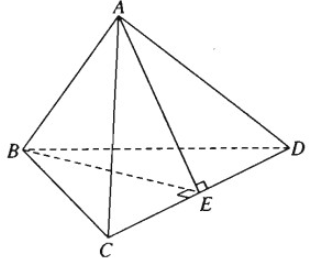
Giả sử AB⊥CD ta phải chứng minh \(A{C^2} + B{{\rm{D}}^2} = A{{\rm{D}}^2} + B{C^2}.\)
Thật vậy, kẻ BE⊥CD tại E, do AB⊥CD ta suy ra CD⊥(ABE) nên CD⊥AE.
Áp dụng định lí Py-ta-go cho các tam giác vuông AEC, BEC, AED và BED ta có:
\( \eqalign{ & A{C^2} = A{{\rm{E}}^2} + C{E^2} \cr & B{{\rm{D}}^2} = B{E^2} + E{{\rm{D}}^2} \cr & B{C^2} = A{{\rm{E}}^2} + E{C^2} \cr & {\rm{A}}{{\rm{D}}^2} = A{E^2} + E{{\rm{D}}^2} \cr} \)
Từ đó ta suy ra \(A{C^2} + B{{\rm{D}}^2} = A{D^2} + B{C^2}\)
Ngược lại nếu tứ diện ABCD có \(A{C^2} + B{{\rm{D}}^2} = A{{\rm{D}}^2} + B{C^2}\)
⇒ \(A{C^2} - A{D^2} = B{C^2} - B{{\rm{D}}^2}.\)
Nếu \(A{C^2} - A{D^2} = B{C^2} - B{{\rm{D}}^2} = {k^2}\):
Trong mặt phẳng (ACD) điểm A thuộc đường thẳng vuông góc với CD tại điểm H trên tia ID với I là trung điểm của CD sao cho \(I{H^2} = {{{k^2}} \over {2C{\rm{D}}}}.\)
Tương tự điểm B thuộc đường thẳng vuông góc với CD cũng tại điểm H nói trên.
Từ đó suy ra CD vuông góc với mặt phẳng (ABH) hay CD⊥AB.
Nếu \(A{C^2} - A{D^2} = B{C^2} - B{{\rm{D}}^2} = - {k^2}\) thì ta có và đưa về trường hợp xét như trên \(A{D^2} - A{C^2} = B{{\rm{D}}^2} - B{C^2} = - {k^2}.\)
1.6. Giải bài 3.46 trang 162 SBT Hình học 11
Cho hình lập phương ABCD.A’B’C’D’. Hãy tính góc của các cặp đường thẳng sau đây:
a) AB’ và BC’
b) AC’ và CD’
Phương pháp giải:
a) Tìm đường thẳng song song với AB' và nằm cùng mp với BC'
⇒ Góc cần tìm tạo bởi đường thẳng đó và BC'.
b) Chứng minh CD’⊥AC’.
Hướng dẫn giải:
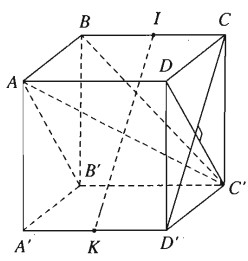
a) Ta có AB' // DC'. Gọi \(\alpha\) là góc giữa AB’và BC’, khi đó \(\alpha = \widehat {DC'B}.\)
Vì tam giác BC’D đều nên \(\alpha = {60^0}\)
b) Gọi \(\beta \) là góc giữa AC’ và CD’.
Vì CD’⊥C’D và CD’⊥AD
( do AD⊥(CDD’C’)
Ta suy ra CD’⊥(ADC’B’)
Vậy CD’⊥AC’ hay \(\beta = {90^0}\)
1.7. Giải bài 3.47 trang 162 SBT Hình học 11
Cho hai tia Ax và By vuông góc với nhau nhận AB làm đoạn vuông góc chung. Gọi M và N là hai điểm di động lần lượt trên Ax và By sao cho AM + BN = MN.
Đặt AB = 2a, gọi O là trung điểm của AB và H là hình chiếu vuông góc điểm O trên đường thẳng MN
a) Chứng minh rằng OH = a, HM = AN, HN = BN.
b) Gọi Bx' là tia song song và cùng chiều với tia Ax và K là hình chiếu vuông góc của H trên mặt phẳng (Bx'; By). Chứng minh BK là phân giác của góc x'By.
c) Chứng minh điểm H nằm trên một đường tròn cố định.
Phương pháp giải:
a) Chứng minh hai tam giác bằng nhau ⇒ đpcm.
b) Chứng minh \(\dfrac{{AM}}{{BN}} = \dfrac{{BM'}}{{BN}}\) ⇒ BK là phân giác của góc x'By.
c) Chứng minh H thuộc đường tròn đường kính AB.
Hướng dẫn giải:
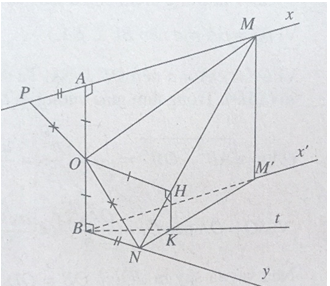
Theo giả thiết ta có M và N là hai điểm di động lần lượt trên hai tia Ax và By sao cho AM + BN = MN.
a) Kéo dài MA một đoạn AP = BN, ta có MP = MN và OP = ON.
Do đó ΔOMP = ΔOMN (c.c.c)
⇒ OA = OH nên OH = a.
Ta suy ra HM = AM và HN = BN.
b) Gọi M’ là hình chiếu vuông góc của điểm M trên mặt phẳng (Bx’, By) ta có:
HK // MM’ với K ∈ NM’.
Khi đó \(\dfrac{{KM'}}{{KN}} = \dfrac{{HM}}{{HN}} = \dfrac{{AM}}{{BN}} = \dfrac{{BM'}}{{BN}}\)
Do đó đối với tam giác BNM’ đường thẳng BK là phân giác của góc (x'By).
c) Gọi (β) là mặt phẳng (AB, BK).
Vì HK // AB nên HK nằm trong mặt phẳng (β) và do đó H thuộc mặt phẳng (β).
Trong mặt phẳng (β) ta có OH = a.
Vậy điểm H luôn luôn nằm trên đường tròn cố định, đường kính AB và nằm trong mặt phẳng cố định (β) = (AB, BK)
1.8. Giải bài 3.48 trang 162 SBT Hình học 11
Hình thoi ABCD tâm O, có cạnh a và có OB = (a√3)/3. Trên đường thẳng vuông góc với mặt phẳng (ABCD) tại O ta lấy một điểm S sao cho SB = a.
a) Chứng minh tam giác SAC là tam giác vuông và SC vuông góc với BD.
b) Chứng minh (SAD) ⊥ (SAB), (SCB) ⊥ (SCD).
c) Tính khoảng cách giữa hai đường thẳng SA và BD.
Phương pháp giải:
a) - Chứng minh tam giác SAC có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó.
- Chứng minh BD vuông góc với mặt phẳng chứa SC.
b) Chứng minh góc giữa hai mặt phẳng bằng 90o.
c) Tìm đoạn thẳng cùng vuông góc với SA và BD.
Hướng dẫn giải:
a) Hai tam giác vuông SOB và AOB có cạnh OB chung và SB = AB = a nên bằng nhau.
Do dó SO = OA = OC nên tam giác SAC vuông tại S.
Mặt khác, vì BD ⊥ AC và BD ⊥ SO nên BD ⊥ (SAC) ⇒ BD ⊥ SC.
b) Gọi I là trung điểm SA.
Vì BS = BA = a nên tam giác BSA cân tại B ⇒ BI ⊥ SA.
Vì DS = DA = a nên DI ⊥ SA.
Mà \(\left( {SAB} \right) \cap \left( {SAD} \right) = SA\) nên góc giữa (SAB) và (SAD) là \(\widehat {BID}.\)
Trong tam giác vuông AOB có:
\( OA = \sqrt {A{B^2} - O{B^2}} = \sqrt {{a^2} - \dfrac{{{a^2}}}{3}} = \dfrac{{a\sqrt 6 }}{3} (vì \ OB = \dfrac{{a\sqrt 3 }}{3} )\)
Vì SO = OA nên \(OI = \dfrac{{OA\sqrt 2 }}{2} = \dfrac{{a\sqrt 6 }}{2}.\dfrac{{\sqrt 2 }}{2} = \dfrac{{a\sqrt 3 }}{3}\)
Do đó OI = OB = OD nên tam giác IBD vuông tại I hay \(\widehat {BID} = {90^0}\)
Vậy \(\left( {SAB} \right) \bot \left( {SAD} \right).\)
Tương tự có \(\left( {SCB} \right) \bot \left( {SCD} \right).\)
c) Dễ thấy OI ⊥ SA do tam giác SOA cân tại O.
Lại có \(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SO\end{array} \right. \Rightarrow BD \bot \left( {SOA} \right) \Rightarrow BD \bot OI\)
Do đó OI là đoạn vuông góc chung của BD và SA.
Vậy \(d\left( {BD,SA} \right) = OI = \dfrac{{a\sqrt 3 }}{3}.\)
2. Bài tập tổng hợp
2.1. Giải bài 3.49 trang 163 SBT Hình học 11
Cho hình chóp tứ giác đều S.ABCD. Gọi M, N lần lượt là trung điểm của SA và SC.
a) Chứng minh AC ⊥ SD
b) Chứng minh MN ⊥ (SBD)
c) Cho AB = SA = a. Tính cosin của góc giữa (SBC) và (ABCD)
Phương pháp giải:
a) Chứng minh AC vuông góc với mặt phẳng chứa SD.
b) Chứng minh MN vuông góc với hai đường thẳng thuộc (SBD).
c) Gọi I là trung điểm của BC. Chứng minh góc giữa (SBC) và (ABCD) là góc SIH.
Hướng dẫn giải:
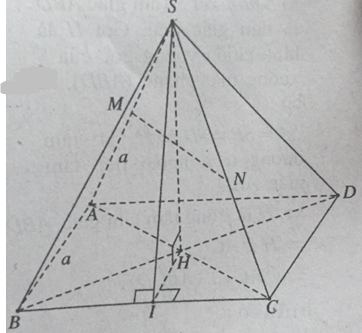
a) Gọi H là tâm hình vuông \(ABCD \Rightarrow SH \bot \left( {ABCD} \right).\)
Ta có: AC ⊥ SH và AC ⊥ BD
⇒ AC ⊥ (SBD) ⇒ AC ⊥ SD.
b) MN là đường trung bình của tam giác SAC nên MN // AC.
Mà AC ⊥ (SBD) ⇒ MN ⊥ (SBD).
c) + Xác định góc α giữa (SBC) và (ABCD)
Gọi I là trung điểm của BC, ta có:
BC ⊥ IH & BC ⊥ SH ⇒ BC ⊥ (SIH)
⇒ BC ⊥ SI.
Ta có:
\(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\\SI \bot BC\\HI \bot BC\end{array} \right.\)
Nên góc giữa (SBC) và (ABCD) là góc giữa SI và HI hay \(\widehat {SIH} = \alpha.\)
+ Tính α:
Ta có: \(IH = \dfrac{1}{2}AB = \dfrac{a}{2}\)
\( SI = \sqrt {S{C^2} - I{C^2}} = \sqrt {{a^2} - \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 3 }}{2} \\ \Rightarrow \cos \alpha = \dfrac{{IH}}{{SI}} = \dfrac{a}{2}:\dfrac{{a\sqrt 3 }}{2} = \dfrac{1}{{\sqrt 3 }}\)
2.2. Giải bài 3.50 trang 163 SBT Hình học 11
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA vuông góc với đáy.
a) Chứng minh tam giác SBC vuông
b) Gọi H là chân đường cao vẽ từ B của tam giác ABC.
Chứng minh (SAC) ⊥ (SBH)
c) Cho AB = a, BC = 2a. Tính khoảng cách từ B đến mặt phẳng (SAC)
Phương pháp giải:
a) Chứng minh BC vuông với SB.
b) Chứng minh (SBH) chứa đường thẳng vuông góc với (SAC).
c) - Dựa vào câu b suy ra d(B, SAC) = BH.
- Áp dụng hệ thức lượng trong tam giác vuông ABC để tính BH.
Hướng dẫn giải:
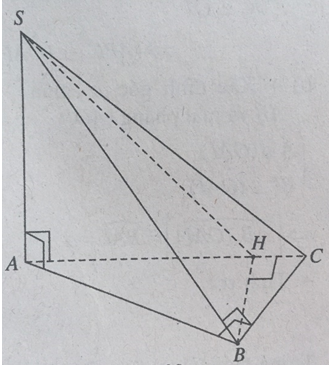
a) Ta có: \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC\)
Mà \(BC \bot AB \ nên \ BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB\)
⇒ Tam giác SBC vuông tại B.
b) Ta có: \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot BH\)
Mà \(BH \bot AC\) nên \(BH \bot \left( {SAC} \right)\)
Lại có \(\left\{ \begin{array}{l}BH \subset \left( {SBH} \right)\\BH \bot \left( {SAC} \right)\end{array} \right. \Rightarrow \left( {SBH} \right) \bot \left( {SAC} \right)\)
c) Do \(BH \bot \left( {SAC} \right)\) nên \(d\left( {B,\left( {SAC} \right)} \right) = BH.\)
Tam giác ABC vuông tại B đường cao BH nên:
\( \dfrac{1}{{B{H^2}}} = \dfrac{1}{{B{A^2}}} + \dfrac{1}{{B{C^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{4{a^2}}} = \dfrac{5}{{4{a^2}}} \\ \Rightarrow B{H^2} = \dfrac{{4{a^2}}}{5} \\ \Rightarrow BH = \dfrac{{2a}}{{\sqrt 5 }} = \dfrac{{2a\sqrt 5 }}{5}\)
2.3. Giải bài 3.51 trang 163 SBT Hình học 11
Cho hình chóp S.ABCD, đáy ABCD là hình thoi cạnh a, góc BAD = 60o, SA = SB = SD = a.
a) Chứng minh (SAC) vuông góc với (ABCD).
b) Chứng minh tam giác SAC vuông.
c) Tính khoảng cách từ S đến (ABCD).
Phương pháp giải:
a) Chứng minh (SAC) chứa đường thẳng vuông góc với đáy.
b) Áp dụng định lí Pytago đảo để chứng minh tam giác SAC vuông.
c) Dựa trên kết quả câu a ⇒ d(S, (ABCD))= SH.
Hướng dẫn giải:
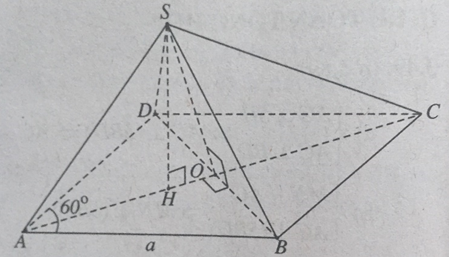
a) Nhận xét: Tam giác ABD là tam giác đều.
Gọi H là hình chiếu vuông góc của S xuống mặt phẳng (ABD), ta có:
SA = SB = SD ⇒ H là tâm đường tròn ngoại tiếp tam giác ABD
⇒ H là trọng tâm tam giác ABD
⇒ H ∈ AC.
\( \Rightarrow SH \subset \left( {SAC} \right)\)
Mà \(SH \bot \left( {ABCD} \right) \Rightarrow \left( {SAC} \right) \bot \left( {ABCD} \right)\)
b) AO là đường cao trong tam giác đều ABD cạnh a nên \(AO = \dfrac{{a\sqrt 3 }}{2}.\)
\( \Rightarrow AH = \dfrac{2}{3}AO = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3} \\ \Rightarrow SH = \sqrt {S{A^2} - A{H^2}} = \sqrt {{a^2} - \dfrac{{{a^2}}}{3}} = \dfrac{{a\sqrt 6 }}{3}\)
Ta có: \(HC = AC - AH = 2AO - AH = 2.\dfrac{{a\sqrt 3 }}{2} - \dfrac{{a\sqrt 3 }}{3} = \dfrac{{2a\sqrt 3 }}{3}\)
\( \Rightarrow SC = \sqrt {S{H^2} + H{C^2}} = \sqrt {\dfrac{{6{a^2}}}{9} + \dfrac{{12{a^2}}}{9}} = a\sqrt 2\)
Tam giác SAC có:
\( S{A^2} + S{C^2} = {a^2} + 2{a^2} = 3{a^2} \)
\(A{C^2} = {\left( {2AO} \right)^2} = {\left( {2.\dfrac{{a\sqrt 3 }}{2}} \right)^2} = 3{a^2}\)
Do đó \(S{A^2} + S{C^2} = A{C^2}\) hay tam giác vuông tại S.
c) Ta có: \(SH \bot \left( {ABCD} \right) \Rightarrow d\left( {S,\left( {ABCD} \right)} \right) = SH = \dfrac{{a\sqrt 6 }}{3}\)
2.4. Giải bài 3.52 trang 163 SBT Hình học 11
Cho tứ diện O.ABC có OA, OB, OC đôi một vuông góc và các cạnh OA = OB = OC = a, gọi I là trung điểm BC.
a) Chứng minh rằng: BC ⊥ (AOI), (OAI) ⊥ (ABC).
b) Tính góc giữa AB và mặt phẳng (AOI).
c) Tính góc giữa các đường thẳng AI và OB.
Phương pháp giải:
a) Chứng minh BC vuông với một đường thẳng thuộc (AOI)
⇒ BC ⊥ (AOI) ⇒ (OAI) ⊥ (ABC)
b) Tìm hình chiếu vuông góc của AB lên (AOI).
⇒ Góc cần tìm là góc tạo bởi hình chiếu với AB.
c) Tìm đường thẳng song song với OB
⇒ Góc cần tìm là góc tạo bởi AI và đường thẳng đó.
Hướng dẫn giải:
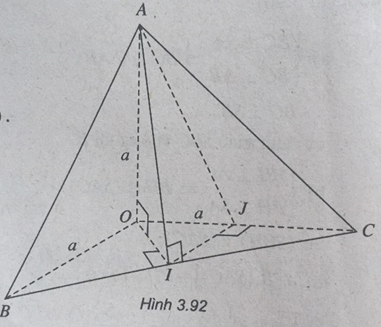
a) Ta có:
\(\left\{ \begin{array}{l}OA \bot OB\\OA \bot OC\end{array} \right. \Rightarrow OA \bot \left( {OBC} \right) \Rightarrow OA \bot BC\)
Mà tam giác OBC vuông cân tại O nên \(OI \bot BC\)
Do đó
\(\left\{ \begin{array}{l}BC \bot OA\\BC \bot OI\end{array} \right. \Rightarrow BC \bot \left( {OAI} \right).\)
Mà \(BC \subset \left( {ABC} \right)\) nên \(\left( {ABC} \right) \bot \left( {OAI} \right).\)
b) Ta có:
\(\left\{ \begin{array}{l}BI \bot OI\\BI \bot OA\end{array} \right. \Rightarrow BI \bot \left( {OAI} \right) \)
⇒ I là hình chiếu của B trên (OAI)
Mà \(BA \cap \left( {OAI} \right) = A\) nên AI là hình chiếu của AB trên (OAI).
Do đó góc giữa AB và (OAI) bằng góc giữa AB và AI hay là góc \(\widehat {BAI}.\)
Tam giác ABC có: AB = BC = AC do các tam giác vuông cân OAB, OAC, OBC bằng nhau.
Do đó ABC là tam giác đều nên \(\widehat A = {60^0}\)
I là trung điểm BC nên AI là phân giác góc A
Nên \(\widehat {BAI} = \dfrac{1}{2}\widehat A = {30^0}.\)
c) Gọi J là trung điểm OC, khi đó IJ // OB
Do \(OB \bot \left( {OAC} \right)\) nên \(IJ \bot \left( {OAC} \right) \Rightarrow IJ \bot AJ\) hay tam giác AIJ vuông tại J.
Vậy góc giữa AI và OB bằng góc giữa AI và IJ hay góc \(\widehat {AIJ}.\)
Có \(IJ = \dfrac{1}{2}OB = \dfrac{a}{2}.\)
\( AJ = \sqrt {O{A^2} + O{J^2}} = \sqrt {{a^2} + \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 5 }}{2}.\)
Tam giác AIJ vuông tại J nên
\(\tan \widehat {AIJ} = \dfrac{{AJ}}{{IJ}} = \dfrac{{a\sqrt 5 }}{2}:\dfrac{a}{2} = \sqrt 5 \Rightarrow \widehat {AIJ} = {65^0}54' \)
2.5. Giải bài 3.53 trang 163 SBT Hình học 11
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a và SA ⊥ (ABCD).
a) Chứng minh BD ⊥ SC.
b) Chứng minh (SAB) ⊥ (SBC).
c) Cho \(SA=\dfrac{a\sqrt6}3 \). Tính góc giữa SC và mặt phẳng (ABCD).
Phương pháp giải:
a) Chứng minh BD vuông góc với mặt phẳng chứa SC ⇒ BD ⊥ SC.
b) Chứng minh (SBC) chứa đường thẳng vuông góc với (SAB).
c) Tìm hình chiếu vuông góc của SC lên mặt đáy
⇒ Góc cần tìm là góc tạo bởi hình chiếu đó và SC.
Hướng dẫn giải:
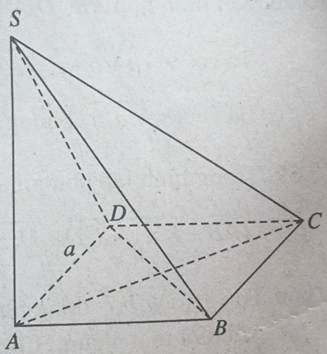
a) Ta có: \(BD \bot AC\) (ABCD là hình vuông)
\( SA \bot \left( {ABCD} \right) \Rightarrow SA \bot BD\)
Do đó
\(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SA\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow BD \bot SC\)
b) Ta có:
\(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right)\)
Mà \(BC \subset \left( {SBC} \right)\) nên \(\left( {SBC} \right) \bot \left( {SAB} \right).\)
c) Vì \(SA \bot \left( {ABCD} \right)\) nên A là hình chiếu của S trên (ABCD).
Mà \(SC \cap \left( {ABCD} \right) = C\) nên AC là hình chiếu của SC trên (ABCD)
Do đó góc giữa SC và (ABCD) bằng góc giữa SC và AC hay là góc \(\widehat {SCA}.\)
Ta có: \( AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2\)
Tam giác SAC vuông tại A nên:
\(\tan \widehat {SCA} = \dfrac{{SA}}{{AC}} = \dfrac{{a\sqrt 6 }}{3}:a\sqrt 2 = \dfrac{{\sqrt 3 }}{3} \Rightarrow \widehat {SCA} = {30^0}.\)
3. Bài tập trắc nghiệm
3.1. Giải bài 3.54 trang 164 SBT Hình học 11
Cho hình hộp ABCD.A'B'C'D' với tâm O. Đẳng thức nào sau đây là Sai?
A. \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \)
B. \(\overrightarrow {AB} + \overrightarrow {BC'} + \overrightarrow {CD} + \overrightarrow {D'A} = \overrightarrow 0 \)
C. \(\overrightarrow {AB} + \overrightarrow {AA'} = \overrightarrow {AD} + \overrightarrow {DD'} \)
D. \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CC'} = \overrightarrow {AD'} + \overrightarrow {D'O} + \overrightarrow {OC'} \)
Phương pháp giải:
Chứng minh từng đáp án để tìm đáp án sai.
Hướng dẫn giải:
\(\overrightarrow {AB} + \overrightarrow {AA'} = \overrightarrow {AD} + \overrightarrow {DD'} \) là sai vì:
\(\begin{array}{l} \overrightarrow {AB} + \overrightarrow {AA'} = \overrightarrow {AB'} \\ \overrightarrow {AD} + \overrightarrow {DD'} = \overrightarrow {AD'} \ne \overrightarrow {AB'}\\ \end{array}\)
Chọn đáp án C.
3.2. Giải bài 3.55 trang 164 SBT Hình học 11
Cho hình lăng trụ tam giác ABC.A'B'C', Đặt \(\overrightarrow {AA'} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b , \overrightarrow {AC} = \overrightarrow c ,\overrightarrow {BC} = \overrightarrow d \). Đẳng thức nào sau đây đúng?
A. \(\overrightarrow a = \overrightarrow b + \overrightarrow c \)
B. \(\overrightarrow a + \overrightarrow b + \overrightarrow c + \overrightarrow d = \overrightarrow 0 \)
C. \(\overrightarrow b + \overrightarrow d - \overrightarrow c = \overrightarrow 0 \)
D. \(\overrightarrow a + \overrightarrow b + \overrightarrow c = \overrightarrow d \)
Phương pháp giải:
Chứng minh từng đáp án để tìm đáp án đúng
Hướng dẫn giải:
\(\overrightarrow b + \overrightarrow d - \overrightarrow c = \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} = \overrightarrow {AA} = \overrightarrow 0 \)
Chọn đáp án C.
3.3. Giải bài 3.56 trang 164 SBT Hình học 11
Cho tứ diện đều ABCD có cạnh bằng a. Khẳng định nào sau đây Sai?
A. \(\overrightarrow {AB} .\overrightarrow {AC} = \dfrac{{{a^2}}}{2}\)
B. \(AB \bot CD \ hay \ \overrightarrow {AB} .\overrightarrow {CD} = \overrightarrow 0 \)
C. \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {DA} = \overrightarrow 0 \)
D. \(\overrightarrow {AC} .\overrightarrow {AD} = \overrightarrow {AC} .\overrightarrow {CD} \)
Phương pháp giải:
Chứng minh từng đáp án để tìm đáp án sai.
Hướng dẫn giải:
Khẳng định \(\overrightarrow {AC} .\overrightarrow {AD} = \overrightarrow {AC} .\overrightarrow {CD} \) là sai vì:
\(\begin{array}{l} \overrightarrow {AC} .\overrightarrow {AD} = \dfrac{{{a^2}}}{2}\\ \overrightarrow {AC} .\overrightarrow {CD} = - \dfrac{{{a^2}}}{2} \end{array}\)
Chọn đáp án D.
3.4. Giải bài 3.57 trang 164 SBT Hình học 11
Khẳng định nào sau đây là đúng?
A. Cho hình chóp S.ABCD. Nếu có \(\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \) thì tứ giác ABCD là hình bình hành.
B. Tứ giác ABCD là hình bình hành nếu \(\overrightarrow {AB} = \overrightarrow {CD}\)
C. Tứ giác ABCD là hình bình hành nếu \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \overrightarrow 0\)
D. Tứ giác ABCD là hình bình hành nếu \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD}\)
Phương pháp giải:
Dựa vào tính chất hình bình hành để tìm khẳng định đúng.
Hướng dẫn giải:
Cho hình chóp S.ABCD.
Nếu có \(\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \) thì tứ giác ABCD có hai đường chéo BD và AC có cùng trung điểm nên là hình bình hành.
Chọn đáp án: A
3.5. Giải bài 3.58 trang 164 SBT Hình học 11
Khẳng định nào sau đây là Sai?
A. Ba vectơ \(\overrightarrow a,\overrightarrow b,\overrightarrow c \) đồng phẳng nếu có một trong ba vectơ đó bằng vectơ \(\overrightarrow 0\)
B. Ba vectơ \(\overrightarrow a,\overrightarrow b,\overrightarrow c \) đồng phẳng nếu có hai trong ba vectơ đó cùng phương.
C. Trong hình hộp ABCD.A'B'C'D' ba vectơ \(\overrightarrow {AB'},\overrightarrow {C'A'},\overrightarrow {DA'} \) đồng phẳng.
D. Vectơ \(\overrightarrow x = \overrightarrow a + \overrightarrow b + \overrightarrow c \) luôn đồng phẳng với hai vectơ \(\overrightarrow a \) và \(\overrightarrow b.\)
Phương pháp giải:
Áp dụng định lí ba vectơ đồng phẳng để xét tính đúng sai
Hướng dẫn giải:
Xét hình hộp ABCD.A'B'C'D", đặt \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {AD} = \overrightarrow b ,\overrightarrow {AA'} = \overrightarrow c \)
Ta có: \(\overrightarrow x = \overrightarrow a + \overrightarrow b + \overrightarrow c = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} =\overrightarrow {AC'} \)
Ba vectơ \(\overrightarrow x ,\overrightarrow a ,\overrightarrow b \) không đồng phẳng.
Chọn đáp án D.
3.6. Giải bài 3.59 trang 164 SBT Hình học 11
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khẳng định nào sau đây là sai?
A. \(\left| {\overrightarrow {AC'} } \right| = a\sqrt 3 \)
B. \(\overrightarrow {AD'} .\overrightarrow {AB'} = {a^2}\)
C. \(\overrightarrow {AB'} .\overrightarrow {CD'} = 0\)
D. \(2\overrightarrow {AB} + \overrightarrow {B'C'} + \overrightarrow {CD} + \overrightarrow {D'A'} = \overrightarrow 0 \)
Phương pháp giải:
Dựa vào tính chất hình lập phương, chứng minh từng đáp áp để tìm đáp án sai.
Hướng dẫn giải:
Trong hình lập phương ABCD.A’B’C’D’ ta có
\( \begin{array}{l}2\overrightarrow {AB} + \overrightarrow {B'C'} + \overrightarrow {CD} + \overrightarrow {D'A'} \\ = \overrightarrow {AB} + \overrightarrow {AB} + \overrightarrow {B'C'} + \overrightarrow {C'D'} + \overrightarrow {D'A'} \\ = \overrightarrow {AB} + \overrightarrow {A'B'} + \overrightarrow {B'C'} + \overrightarrow {C'D'} + \overrightarrow {D'A'} \\ = \overrightarrow {AB} + \left( {\overrightarrow {A'B'} + \overrightarrow {B'C'} + \overrightarrow {C'D'} + \overrightarrow {D'A'} } \right)\\ = \overrightarrow {AB} + \overrightarrow 0 \\ = \overrightarrow {AB} \ne \overrightarrow 0 \end{array}\)
Chọn đáp án: D
3.7. Giải bài 3.60 trang 165 SBT Hình học 11
Khẳng định nào sau đây là Sai?
A. Cho hai vectơ không cùng phương \(\overrightarrow a\) và \(\overrightarrow b\). Khi đó ba vectơ \(\overrightarrow a,\overrightarrow b,\overrightarrow c \) đồng phẳng khi và chỉ khi có cặp số m, n sao cho \(\overrightarrow c = m\overrightarrow a + n\overrightarrow b\), ngoài ra cặp số m, n là duy nhất.
B. Nếu có \(m\overrightarrow a + n\overrightarrow b + p\overrightarrow c = \overrightarrow 0 \) và một trong ba số m, n, p khác 0 thì ba vectơ \(\overrightarrow a,\overrightarrow b,\overrightarrow c \) đồng phẳng.
C. Ba vectơ \(\overrightarrow a,\overrightarrow b,\overrightarrow c \) đồng phẳng khi và chỉ khi ba vectơ đó cùng có giá thuộc một mặt phẳng.
D. Ba tia Ox, Oy, Oz vuông góc với nhau từng đôi một thì ba tia đó không đồng phẳng.
Phương pháp giải:
Áp dụng định lý ba vectơ đồng phẳng để tìm khẳng định sai.
Hướng dẫn giải:
Ba vectơ đồng phẳng khi và chỉ khi ba vectơ đó có giá cùng song song hoặc nằm trên một mặt phẳng.
Chọn đáp án: C
3.8. Giải bài 3.61 trang 165 SBT Hình học 11
Cho hai điểm phân biệt A, B và một điểm O bất kì. Khẳng định nào sau đây là đúng?
A. Điểm M thuộc đường thẳng AB khi và chỉ khi \(\overrightarrow {OM} = \overrightarrow {OB} = k\overrightarrow {BA}\)
B. Điểm M thuộc đường thẳng AB khi và chỉ khi \(\overrightarrow {OM} = \overrightarrow {OB} = k\left( {\overrightarrow {OB} - \overrightarrow {OA} } \right)\)
C. Điểm M thuộc đường thẳng AB khi và chỉ khi \(\overrightarrow {OM} = k\overrightarrow {OA} + \left( {1 - k} \right)\overrightarrow {OB}\)
D. Điểm M thuộc đường thẳng AB khi và chỉ khi \(\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {OB}\)
Phương pháp giải:
Áp dụng quy tắc ba điểm để tìm đẳng thức đúng.
Hướng dẫn giải:
\(\begin{array}{l} \overrightarrow {OM} = k\overrightarrow {OA} + \left( {1 - k} \right)\overrightarrow {OB} \\ \Leftrightarrow \overrightarrow {OM} \left( {k + 1 - k} \right) = k\overrightarrow {OA} + \left( {1 - k} \right)\overrightarrow {OB} \\ \Leftrightarrow \overrightarrow 0 = k\left( {\overrightarrow {OA} - \overrightarrow {OM} } \right) + \left( {1 - k} \right)\left( {\overrightarrow {OB} - \overrightarrow {OM} } \right)\\ \Leftrightarrow \overrightarrow 0 = k\overrightarrow {MA} + \left( {1 - k} \right)\overrightarrow {MB} \end{array}\)
⇒ Điểm M thuộc đường thẳng AB.
Chọn đáp án: C
3.9. Giải bài 3.62 trang 165 SBT Hình học 11
Khẳng định nào sau đây là đúng?
A. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song với nhau.
C. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thứ ba thì song song với nhau.
D. Mặt phẳng (α) và đường thẳng a cùng vuông góc với đường thẳng b thì song song với nhau.
Phương pháp giải:
Suy luận từng đáp án để tìm đáp án sai.
Hướng dẫn giải:
Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau ⇒ Đúng.
Chọn đáp án: A
3.10. Giải bài 3.63 trang 165 SBT Hình học 11
Với a, b, c là các đường thẳng, khẳng định nào sau đây là Sai?
A. Nếu a ⊥ b và b ⊥ c thì a // c;
B. Nếu a// b và b ⊥ c thì a ⊥ c;
C. Nếu a vuông góc với mặt phẳng (α) và b song song với mặt phẳng (α) thì a ⊥ b;
D. Nếu a ⊥ b, c ⊥ b và a cắt c thì b vuông góc với mặt phẳng (a, c)
Phương pháp giải:
Suy luận từng đáp án để tìm đáp án sai, cho ví dụ đáp án sai.
Hướng dẫn giải:
Khẳng định “Nếu a ⊥ b và b ⊥ c thì a // c” là SAI vì có thể xảy ra \(b \bot \left( {a,c} \right)\) (trường hợp a,c cắt nhau).
Chọn đáp án: A
3.11. Giải bài 3.64 trang 166 SBT Hình học 11
Cho các mệnh đề sau với (α) và (β) là hai mặt phẳng vuông góc với nhau với giao tuyến m = (α) ∩ (β) và a, b, c, d là các đường thẳng. Khẳng định nào sau đây là đúng?
A. Nếu a ⊂ (α) và a ⊥ m thì a ⊥ (β).
B. Nếu b ⊥ m thì b ⊂ (α) hoặc b ⊂ (β).
C. Nếu c // m thì c // (α) hoặc c // (β).
D. Nếu d ⊥ m thì d ⊥ (α)
Phương pháp giải:
Suy luận từ đáp án để tìm đáp án đúng.
Hướng dẫn giải:
Khẳng định “Nếu a ⊂ (α) và a ⊥ m thì a ⊥ (β) là đúng.
Chọn đáp án: A
3.12. Giải bài 3.65 trang 166 SBT Hình học 11
Cho a, b, c là các đường thẳng. Khẳng định nào sau đây là đúng?
A. Nếu a ⊥ b và mặt phẳng (α) chứa a; mặt phẳng (β) chứa b thì (α) ⊥ (β)
B. Cho a ⊥ b và b nằm trong mặt phẳng (α). Mọi mặt phẳng (β) chứa a và vuông góc với b thì (β) ⊥ (α)
C. Cho a ⊥ b. Mọi mặt phẳng chứa b đều vuông góc với a.
D. Cho a // b. Mọi mặt phẳng (α) chứa c trong đó c ⊥ a và c ⊥ b thì đều vuông góc với mặt phẳng (a, b).
Phương pháp giải:
Suy luận từ đáp án để tìm đáp án đúng.
Hướng dẫn giải:
Khẳng định “Cho a ⊥ b và b nằm trong mặt phẳng (α). Mọi mặt phẳng (β) chứa a và vuông góc với b thì (β) ⊥ (α) là đúng.
Chọn đáp án: B
3.13. Giải bài 3.66 trang 166 SBT Hình học 11
Khẳng định nào sau đây là đúng?
A. Qua một đường thẳng, có duy nhất một mặt phẳng vuông góc với một đường thẳng khác.
B. Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
C. Cho hai đường thẳng a và b vuông góc với nhau. Nếu mặt phẳng (α) chứa a và mặt phẳng (β) chứa b thì (α) ⊥ (β).
D. Cho hai đường thẳng chéo nhau a và b đồng thời a ⊥ b. Luôn có mặt phẳng (α) chứa a để (α) ⊥ b.
Phương pháp giải:
Suy luận từ đáp án để tìm đáp án đúng, cho ví dụ đáp án sai.
Hướng dẫn giải:
Đáp án A sai vì phải có giả thiết hai đường thẳng đó vuông góc.
Đáp án B sai vì có vô số mặt phẳng.
Đáp án C sai vì có trường hợp a \bot b,a \cap b = I và hai mặt phẳng \left( \alpha \right),\left( \beta \right) trùng nhau cùng chứa a,b.
Chọn đáp án: D
3.14. Giải bài 3.67 trang 166 SBT Hình học 11
Khẳng định nào sau đây là đúng?
A. Cho hai đường thẳng a và b vuông góc với nhau, nếu mặt phẳng (α) chứa a và mặt phẳng (β) chứa b thì (α) ⊥ (β)
B. Cho đường thẳng a vuông góc với mặt phẳng (α), mọi mặt phẳng (β) chứa a thì (β)⊥(α)
C. Cho hai đường thẳng a và b vuông góc với nhau, mặt phẳng nào vuông góc với đường này thì song song với đường kia.
D. Cho hai đường thẳng chéo nhau a và b, luôn luôn có một mặt phẳng chứa đường này và vuông góc với đường thẳng kia.
Phương pháp giải:
Suy luận từ đáp án để tìm đáp án đúng.
Hướng dẫn giải:
Chỉ có khẳng định B là đúng: “Cho đường thẳng a vuông góc với mặt phẳng (α), mọi mặt phẳng (β) chứa a thì (β) ⊥ (α).
Chọn đáp án: B
3.15. Giải bài 3.68 trang 167 SBT Hình học 11
Cho tứ diện đều ABCD. Khoảng cách từ điểm D tới mặt phẳng (ABC) KHÔNG BẰNG độ dài đoạn thẳng nào dưới đây?
A. Đoạn nối từ D đến trọng tâm của tam giác ABC
B. Đoạn nối từ D đến hình chiếu vuông góc của điểm D trên mặt phẳng (ABC)
C. Đoạn nối từ D đến tâm đường tròn ngoại tiếp tam giác ABC
D. Đoạn nối từ D đến trung điểm của đoạn AM với M là trung điểm của đoạn BC.
Phương pháp giải:
Dựa vào tính chất của tứ diện đều để tìm ra hình chiếu của D trên (ABC)
⇒ Tìm đáp án sai.
Hướng dẫn giải:
Do tam giác ABC đều và tứ diện ABCD đều nên gọi H là hình chiếu của D trên (ABC)
⇒ H là tâm đường tròn ngoại tiếp tam giác ABC, cũng là trọng tâm tam giác nên A, B, C đúng.
Chỉ có khẳng định D là SAI: “ Độ dài đoạn DI trong đó I là trung điểm của đoạn AM với M là trung điểm của đoạn BC”.
Chọn đáp án: D
3.16. Giải bài 3.69 trang 167 SBT Hình học 11
Cho hình lập phương ABCD.A'B'C'D' cạnh a Khẳng định nào sau đây là đúng?
A. Khoảng cách từ điểm A đến mặt phẳng (A'BD) bằng \(\dfrac13\)
B. Độ dài đoạn AC' bằng \(a\sqrt3\)
C. Khoảng cách từ điểm A đến mặt phẳng (CDD'C') bằng \(a\sqrt2\)
D. Khoảng cách từ điểm A đến mặt phẳng (BCC'B') bằng \(\dfrac{3a}2\)
Phương pháp giải:
Tính từng khoảng cách và chọn đáp án đúng.
Hướng dẫn giải:
Độ dài đoạn AC’ bằng \(a\sqrt3\)
Chọn đáp án: B
3.17. Giải bài 3.70 trang 167 SBT Hình học 11
Khoảng cách giữa hai cạnh đối trong một tứ diện đều cạnh a là
A. \(\dfrac{a\sqrt2}2\) B. \(\dfrac{a\sqrt3}3\)
C. \(\dfrac{2a}3\) D. 2a
Phương pháp giải:
Khoảng cách cần tìm bằng độ dài đoạn thẳng nối hai trung điểm của hai cạnh đó.
Hướng dẫn giải:
Xét tứ diện đều ABCD, gọi M, N lần lượt là trung điểm của cặp cạnh đối AB và CD.
Khi đó MN là khoảng cách cần tìm.
Ta có tam giác AMN vuông tại M, do đó:
\( MN = \sqrt {A{N^2} - A{M^2}} = \sqrt {\dfrac{{3{a^2}}}{4} - \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 2 }}{2}\)
Chọn đáp án: A
3.18. Giải bài 3.71 trang 167 SBT Hình học 11
Hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Khoảng cách từ đỉnh S tới mặt phẳng đáy là
A. 1,5a B. a
C. \(a\sqrt2\) D. \(a\sqrt3\)
Phương pháp giải:
Khoảng cách cần tìm bằng độ dài đoạn thẳng nối S và trọng tâm tam giác ABC.
Hướng dẫn giải:
Tam giác ABC đều cạnh 3a nên chiều cao tam giác là \(\dfrac{{3a\sqrt 3 }}{2}.\)
Gọi G là trọng tâm tam giác ABC, ta có \(AG = \dfrac{2}{3}.\dfrac{{3a\sqrt 3 }}{2} = a\sqrt 3.\)
Trong tam giác vuông SAG ta có:
\( SG = \sqrt {S{A^2} - A{G^2}} = \sqrt {4{a^2} - 3{a^2}} = a\)
Vậy khoảng cách từ đỉnh S tới mặt phẳng đáy là SG = a.
Chọn đáp án: B
3.19. Giải bài 3.72 trang 167 SBT Hình học 11
Khẳng định nào sau đây là đúng?
A. Đường thẳng vuông góc chung của hai đường thẳng a và b chéo nhau là một đường thẳng d vừa vuông góc với a và vừa vuông góc với b.
B. Đoạn vuông góc chung của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn nối hai điểm bất kì lần lượt nằm trên hai đường ấy là ngược lại.
C. Cho hai đường thẳng chéo nhau a và b. Đường vuông góc chung luôn luôn nằm trong mặt phẳng vuông góc với a và chứa đường thẳng b.
D. Hai đường thẳng chéo nhau là hai đường thẳng không song song với nhau.
Phương pháp giải:
Dựa vào định nghĩa đường vuông góc chung để tìm đáp án đúng.
Hướng dẫn giải:
Chỉ có khẳng định B là đúng: “Đoạn vuông góc chung của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn nối hai điểm bất kì lần lượt nằm trên hai đường thẳng ấy và ngược lại”.
Chọn đáp án: B
3.20. Giải bài 3.73 trang 168 SBT Hình học 11
Cho hình hộp ABCD.A'B'C'D' có ba kích thước AB = a, AD = b, AA' = c. Khẳng định nào sau đây là SAI?
A. Độ dài đường chéo BD' bằng \(\sqrt {{a^2} + {b^2} + {c^2}}\)
B. Khoảng cách giữa hai đường thẳng AB và CC' bằng b.
C. Khoảng cách giữa hai đường thẳng BB' và DD' bằng \(\sqrt {{a^2} + {b^2}}.\)
D. Khoảng cách từ A đến mặt phẳng (A'BD) bằng \(\dfrac{1}{3}\sqrt {{a^2} + {b^2} + {c^2}}\)
Phương pháp giải:
Tính từng độ dài, khoảng cách ở các đáp án để tìm đáp án sai.
Hướng dẫn giải:
Khẳng định D là SAI vì khoảng cách d từ điểm A đến mặt phẳng (A’BD) được tính bởi công thức:
\( \dfrac{1}{{{d^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}} + \dfrac{1}{{{c^2}}} \\ \Leftrightarrow d = \dfrac{{abc}}{{\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }}\)
Chọn đáp án: D
Tham khảo thêm
- doc Giải bài tập SBT Toán 11 Bài 1: Vectơ trong không gian
- doc Giải bài tập SBT Toán 11 Bài 2: Hai đường thẳng vuông góc
- doc Giải bài tập SBT Toán 11 Bài 3: Đường thẳng vuông góc với mặt phẳng
- doc Giải bài tập SBT Toán 11 Bài 4: Hai mặt phẳng vuông góc
- doc Giải bài tập SBT Toán 11 Bài 5: Khoảng cách
