Giải bài tập SBT Toán 11 Bài 1: Vectơ trong không gian
eLib xin giới thiệu đến quý thầy cô giáo và các em học sinh nội dung giải bài tập SBT môn Hình học 11 bên dưới đây, tài liệu cung cấp cho các em hệ thống 7 bài tập trang 129-130 với đầy đủ phương pháp và hướng dẫn giải giúp các em ôn tập và hệ thống lại toàn bộ kiến thức đã học trong bài Vectơ trong không gian. Mời các em tham khảo!
Mục lục nội dung

1. Giải bài 3.1 trang 129 SBT Hình học 11
Cho hình lập phương ABCDA’B’C’D’ cạnh a. Gọi O và O’ theo thứ tự là tâm của hai hình vuông ABCD và A’B’C’D’.
a) Hãy biểu diễn các vectơ \(\overrightarrow {AO},\overrightarrow {AO'} \) theo các vectơ có điểm đầu và điểm cuối là các đỉnh của hình lập phương đã cho.
b) Chứng minh rằng \(\overrightarrow {A{\rm{D}}} + \overrightarrow {D'C'} + \overrightarrow {D'A'} = \overrightarrow {AB}.\)
Phương pháp giải:
Xen các điểm thức hợp và sử dụng các tính chất cộng véc tơ, quy tắc trung điểm,... để biểu diễn một véc tơ qua ba véc tơ không đồng phẳng trong không gian.
Hướng dẫn giải:
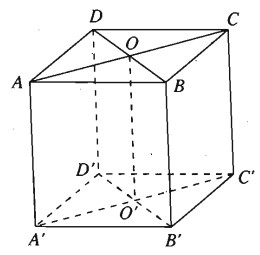
a) Ta có:
\( \displaystyle \overrightarrow {AO} = {1 \over 2}\overrightarrow {AC} = {1 \over 2}\overrightarrow {A'C'} \displaystyle = {1 \over 2}\left( {\overrightarrow {AB} + \overrightarrow {A{\rm{D}}} } \right) \\ \displaystyle \overrightarrow {AO} = \overrightarrow {AB} + \overrightarrow {BO} = \overrightarrow {AB} + {1 \over 2}\overrightarrow {B{\rm{D}}} \)
\(\\ \displaystyle \overrightarrow {AO} = {1 \over 2}\overrightarrow {AC} + \overrightarrow {AA'}\)
\( \displaystyle \eqalign{ & = {1 \over 2}\left( {\overrightarrow {AA'} + \overrightarrow {AC'} } \right) = {1 \over 2}\left( {\overrightarrow {AB'} + \overrightarrow {AD'} } \right) \cr & = \overrightarrow {AA'} + \overrightarrow {A'B'} + {1 \over 2}\overrightarrow {B'D'} \cr & = \overrightarrow {AB} + \overrightarrow {BB'} + {1 \over 2}\overrightarrow {B'D'} \cr}\)
b) Ta có:
\(\displaystyle \overrightarrow {AD} + \overrightarrow {D'C'} + \overrightarrow {D'A'} \displaystyle = \overrightarrow {AD} + \overrightarrow {DC} + \overrightarrow {CB} \\(vì\ \displaystyle \overrightarrow {D'C'} = \overrightarrow {DC} \ và \ \displaystyle \overrightarrow {D'A'} = \overrightarrow {CB} ) \ nên \ \displaystyle \overrightarrow {A{\rm{D}}} + \overrightarrow {D'C'} + \overrightarrow {D'A'} = \overrightarrow {AB}.\)
2. Giải bài 3.2 trang 129 SBT Hình học 11
Trong không gian cho điểm O và bốn điểm A, B, C, D phân biệt và không thẳng hàng. Chứng minh rằng điều kiện cần và đủ để bốn điểm A, B, C, D tạo thành một hình bình hành là: \( \overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow {OB} + \overrightarrow {O{\rm{D}}}\)
Phương pháp giải:
ABCD là hình bình hành nếu và chỉ nếu \(\overrightarrow {BC} = \overrightarrow {A{\rm{D}}} \)
Hướng dẫn giải:
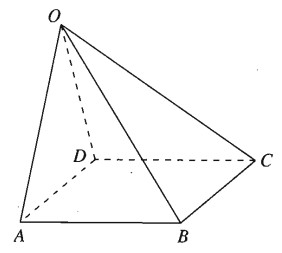
Giả sử bốn điểm A, B, C, D tạo thành một hình bình hành ta có:
\( \overrightarrow {BC} = \overrightarrow {A{\rm{D}}} \\ \Leftrightarrow \overrightarrow {OC} - \overrightarrow {OB} = \overrightarrow {O{\rm{D}}} - \overrightarrow {OA} \)
(với điểm O bất kì )
\( \Leftrightarrow \overrightarrow {OC} + \overrightarrow {OA} = \overrightarrow {O{\rm{D}}} + \overrightarrow {OB}\)
Ngược lại, giả sử ta có hệ thức:
\( \overrightarrow {OC} + \overrightarrow {OA} = \overrightarrow {O{\rm{D}}} + \overrightarrow {OB} \\ \Leftrightarrow \overrightarrow {OC} - \overrightarrow {OB} = \overrightarrow {O{\rm{D}}} - \overrightarrow {OA} \\ \Leftrightarrow \overrightarrow {BC} = \overrightarrow {A{\rm{D}}} \)
Vì A, B, C, D không thẳng hàng nên tứ giác ABCD là hình bình hành.
3. Giải bài 3.3 trang 129 SBT Hình học 11
Cho tứ diện ABCD. Gọi P và Q lần lượt là trung điểm của các cạnh AB và CD. Trên các cạnh AC và BD lần lượt ta lấy các điểm M, N sao cho \( \displaystyle {{AM} \over {AC}} = {{BN} \over {B{\rm{D}}}} = k\left( {k > 0} \right)\).Chứng minh rằng ba vectơ \(\displaystyle \overrightarrow {PQ},\overrightarrow {PM},\overrightarrow {PN} \) đồng phẳng.
Phương pháp giải:
Chứng minh \(\displaystyle \overrightarrow {PQ} = m\overrightarrow {PM} +n\overrightarrow {PN} \) và sử dụng điều kiện đồng phẳng của ba véctơ và kết luận.
Hướng dẫn giải:
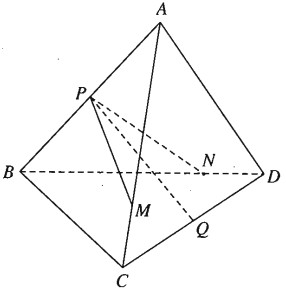
Ta có:
\( \displaystyle \eqalign{ & \overrightarrow {PQ} = {1 \over 2}\left( {\overrightarrow {PC} + \overrightarrow {P{\rm{D}}} } \right) \cr & = {1 \over 2}\left[ {\left( {\overrightarrow {AC} - \overrightarrow {AP} } \right) + \left( {\overrightarrow {B{\rm{D}}} - \overrightarrow {BP} } \right)} \right] \cr & = {1 \over 2}\left[ {\left( {\overrightarrow {AC} + \overrightarrow {B{\rm{D}}} } \right) - \underbrace {\left( {\overrightarrow {AP} + \overrightarrow {BP} } \right)}_{\overrightarrow 0 }} \right] \cr & = {1 \over 2}.{1 \over k}\left( {\overrightarrow {AM} + \overrightarrow {BN} } \right) \cr} \)
Vì \(\displaystyle \overrightarrow {AC} = {1 \over k}.\overrightarrow {AM} \) và \(\displaystyle \overrightarrow {B{\rm{D}}} = {1 \over k}.\overrightarrow {BN}\)
Đồng thời \(\displaystyle \overrightarrow {AM} = \overrightarrow {AP} + \overrightarrow {PM} \) và \(\displaystyle \overrightarrow {BN} = \overrightarrow {BP} + \overrightarrow {PN}\)
Nên \(\displaystyle \overrightarrow {PQ} = {1 \over {2k}}\left( {\overrightarrow {PM} + \overrightarrow {PN} } \right) \) vì \( \displaystyle \overrightarrow {AP} + \overrightarrow {BP} = \overrightarrow 0\)
Vậy \(\displaystyle \overrightarrow {PQ} = {1 \over {2k}}\overrightarrow {PM} + {1 \over {2k}}\overrightarrow {PN}\)
Do đó ba vectơ \(\displaystyle \overrightarrow {PQ},\overrightarrow {PM},\overrightarrow {PN} \) đồng phẳng.
4. Giải bài 3.4 trang 130 SBT Hình học 11
Cho hình lăng trụ tam giác ABC.A’B’C’ có độ dài cạnh bên bằng a. Trên các cạnh bên AA’,BB’,CC’ ta lấy tương ứng các điểm M, N, P sao cho AM + BN + CP = a
Chứng minh rằng mặt phẳng (MNP) luôn luôn đi qua một điểm cố định.
Phương pháp giải:
Gọi G' là trọng tâm tam giác MNP và chứng minh G' cố định.
Hướng dẫn giải:
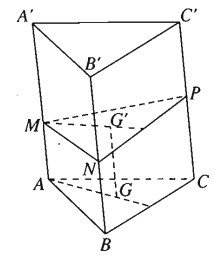
Gọi G và G’ lần lượt là trọng tâm của tam giác ABC và tam giác MNP. Ta có:
\( \displaystyle \eqalign{ & \,\,\,\,\overrightarrow {GG'} = \overrightarrow {GA} + \overrightarrow {AM} + \overrightarrow {MG'} \cr & + \,\,\overrightarrow {GG'} = \overrightarrow {GB} + \overrightarrow {BN} + \overrightarrow {NG'} \cr & \,\,\,\,\,\overrightarrow {GG'} = \overrightarrow {GC} + \overrightarrow {CP} + \overrightarrow {PG'} \cr}\)
Cộng từng vế với vế ta có:
\( \displaystyle 3\overrightarrow {GG'} = \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right) \displaystyle + \left( {\overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CP} } \right) \displaystyle + \left( {\overrightarrow {MG'} + \overrightarrow {NG'} + \overrightarrow {PG'} } \right)\)
Vì G là trọng tâm của tam giác ABC nên \(\displaystyle \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0\)
G’ là trọng tâm của tam giác MNP nên \(\displaystyle \overrightarrow {MG'} + \overrightarrow {NG'} + \overrightarrow {PG'} = \overrightarrow 0.\)
Do đó: \(\displaystyle 3\overrightarrow {GG'} = \overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CP}\)
Hay \(\displaystyle \overrightarrow {GG'} = {1 \over 3}\left( {\overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CP} } \right) \displaystyle = {1 \over 3}\overrightarrow {AA'}\)
Vì điểm G cố định và \(\displaystyle {1 \over 3}\overrightarrow {AA'} \) là vectơ không đổi nên G’ là điểm cố định.
Vậy mặt phẳng (MNP) luôn luôn đi qua điểm G’ cố định.
5. Giải bài 3.5 trang 130 SBT Hình học 11
Trong không gian cho hai hình bình hành ABCD và A’B’C’D’ chỉ có chung nhau một điểm A. Chứng minh rằng các vectơ \(\overrightarrow {BB'},\overrightarrow {CC'},\overrightarrow {DD'} \) đồng phẳng.
Phương pháp giải:
Chứng minh rằng \(\overrightarrow {BB'} + \overrightarrow {DD'} = \overrightarrow {CC'} \) suy ra điều phải chứng minh.
Hướng dẫn giải:
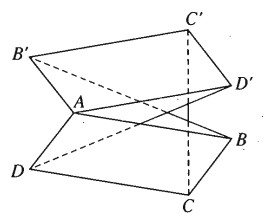
Ta có :
\( \overrightarrow {BB'} = \overrightarrow {BA} + \overrightarrow {AB'} \\ \overrightarrow {DD'} = \overrightarrow {DA} + \overrightarrow {AD'} \)
Do đó \(\overrightarrow {BB'} + \overrightarrow {DD'} = \left( {\overrightarrow {BA} + \overrightarrow {DA} } \right) + \left( {\overrightarrow {AB'} + \overrightarrow {AD'} } \right)\)
Vì \(\overrightarrow {BA} = \overrightarrow {C{\rm{D}}} \) và \( \overrightarrow {AB'} + \overrightarrow {AD'} = \overrightarrow {AC'}\)
Nên \(\overrightarrow {BB'} + \overrightarrow {DD'} = \left( {\overrightarrow {C{\rm{D}}} + \overrightarrow {DA} } \right) + \overrightarrow {AC'}\)
Vậy \(\overrightarrow {BB'} + \overrightarrow {DD'} = \overrightarrow {CA} + \overrightarrow {AC'} = \overrightarrow {CC'}\)
Hệ thức \(\overrightarrow {BB'} + \overrightarrow {DD'} = \overrightarrow {CC'} \) biểu thị sự đồng phẳng của ba vectơ \(\overrightarrow {BB'},\overrightarrow {CC'},\overrightarrow {DD'}.\)
6. Giải bài 3.6 trang 130 SBT Hình học 11
Trên mặt phẳng \(\displaystyle \left( \alpha \right)\) cho hình bình hành \(\displaystyle {A_1}{B_1}{C_1}{D_1}\). Về một phía đối với mặt phẳng \(\displaystyle \left( \alpha \right)\) ta dựng hình bình hành \(\displaystyle {A_2}{B_2}{C_2}{D_2}\). Trên các đoạn \(\displaystyle {A_1}{A_2},{B_1}{B_2},{C_1}{C_2},{D_1}{D_2}\) ta lần lượt lấy các điểm A, B, C, D sao cho \( \displaystyle {{A{A_1}} \over {A{A_2}}} = {{B{B_1}} \over {B{B_2}}} = {{C{C_1}} \over {C{C_2}}} = {{D{D_1}} \over {D{D_2}}} = 3\). Chứng minh rằng tứ giác \displaystyle ABCD là hình bình hành.
Phương pháp giải:
- Lấy điểm O cố định.
- Điều kiện cần và đủ để ABCD là hình bình hành là \(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow {OB} + \overrightarrow {O{\rm{D}}}\) (theo bài tập 3.2).
Hướng dẫn giải:
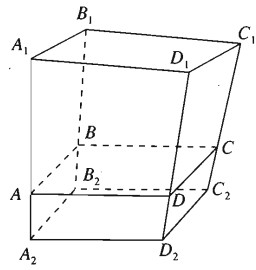
Lấy điểm O cố định rồi đặt \(\overrightarrow {O{A_1}} = \overrightarrow {{a_1}},\,\,\overrightarrow {O{B_1}} = \overrightarrow {{b_1}},\,\,\overrightarrow {O{C_1}} = \overrightarrow {{c_1}},\,\,\overrightarrow {O{D_1}} = \overrightarrow {{d_1}}\).
Điều kiện cần và đủ để tứ giác \({A_1}{B_1}{C_1}{D_1}\) là hình bình hành là \(\overrightarrow {{a_1}} + \overrightarrow {{c_1}} = \overrightarrow {{b_1}} + \overrightarrow {{d_1}} \) ( theo bài tập 3.2) (1)
Đặt \(\overrightarrow {O{A_2}} = \overrightarrow {{a_2}},\overrightarrow {O{B_2}} = \overrightarrow {{b_2}}, \overrightarrow {O{C_2}} = \overrightarrow {{c_2}},\overrightarrow {O{D_2}} = \overrightarrow {{d_2}}.\)
Điều kiện cần và đủ để tứ giác \({A_2}{B_2}{C_2}{D_2}\) là hình bình hành là \(\overrightarrow {{a_2}} + \overrightarrow {{c_2}} = \overrightarrow {{b_2}} + \overrightarrow {{d_2}} \) (2)
Đặt \(\overrightarrow {OA} = \overrightarrow a,\,\,\overrightarrow {OB} = \overrightarrow b,\,\,\overrightarrow {OC} = \overrightarrow c,\,\,\overrightarrow {OD} = \overrightarrow d.\)
Ta có \({{A{A_1}} \over {A{A_2}}} = 3 \Rightarrow \overrightarrow {A{A_1}} = - 3\overrightarrow {A{A_2}}\)
\( \eqalign{ & \Leftrightarrow \overrightarrow {O{A_1}} - \overrightarrow {OA} = 3\left( {\overrightarrow {O{A_2}} - \overrightarrow {OA} } \right) \cr & \Leftrightarrow \overrightarrow {{a_1}} - \overrightarrow a = - 3\left( {\overrightarrow {{a_2}} - \overrightarrow a } \right) \cr & \Leftrightarrow \overrightarrow a = {1 \over 4}\left( {\overrightarrow {{a_1}} + 3\overrightarrow {{a_2}} } \right) \cr}\)
Tương tự:
\(\overrightarrow b = {1 \over 4}\left( {\overrightarrow {{b_1}} + 3\overrightarrow {{b_2}} } \right), \overrightarrow c = {1 \over 4}\left( {\overrightarrow {{c_1}} + 3\overrightarrow {{c_2}} } \right),\overrightarrow {\,\,d} = {1 \over 4}\left( {\overrightarrow {{d_1}} + 3\overrightarrow {{d_2}} } \right).\)
Ta có:
\(\overrightarrow a + \overrightarrow c \\= {1 \over 4}\left( {\overrightarrow {{a_1}} + 3\overrightarrow {{a_2}} } \right) + {1 \over 4}\left( {\overrightarrow {{c_1}} + 3\overrightarrow {{c_2}} } \right) \\= {1 \over 4}\left( {\overrightarrow {{a_1}} + \overrightarrow {{c_1}} } \right) + {3 \over 4}\left( {\overrightarrow {{a_2}} + \overrightarrow {{c_2}} } \right)\)
Và:
\( \eqalign{ & \overrightarrow b + \overrightarrow d = {1 \over 4}\left( {\overrightarrow {{b_1}} + 3\overrightarrow {{b_2}} } \right) + {1 \over 4}\left( {\overrightarrow {{d_1}} + 3\overrightarrow {{d_2}} } \right) \cr & = {1 \over 4}\left( {\overrightarrow {{b_1}} + \overrightarrow {{d_1}} } \right) + {3 \over 4}\left( {\overrightarrow {{b_2}} + \overrightarrow {{d_2}} } \right) \cr}\)
Từ (1) và (2) ta có \(\overrightarrow {{a_1}} + \overrightarrow {{c_1}} = \overrightarrow {{b_1}} + \overrightarrow {{d_1}} \) và \( \overrightarrow {{a_2}} + \overrightarrow {{c_2}} = \overrightarrow {{b_2}} + \overrightarrow {{d_2}} \) nên suy ra:
\( \overrightarrow a + \overrightarrow b + \overrightarrow c + \overrightarrow d \Leftrightarrow \overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow {OB} + \overrightarrow {O{\rm{D}}}\)
Vậy tứ giác ABCD là hình bình hành.
7. Giải bài 3.7 trang 130 SBT Hình học 11
Cho hình hộp ABCD.A’B’C’D’ có P và R lần lượt là trung điểm các cạnh AB và A’D’. Gọi P’, Q, Q’,R' lần lượt là tâm đối xứng của các hình bình hành ABCD, CDD’C’, A’B’C’D’, ADD’A’
a) Chứng minh rằng \(\overrightarrow {PP'} + \overrightarrow {QQ'} + \overrightarrow {R{\rm{R}}'} = \overrightarrow 0\)
b) Chứng minh hai tam giác PQR và P’Q’R’ có trọng tâm trùng nhau.
Phương pháp giải:
a) Biểu diễn các véc tơ trong biểu thức cần chứng minh về các véctơ cơ sở của hình hộp và tính toán.
b) Sử dụng kết quả câu a, chú ý gọi G, G' là các trọng tâm rồi chứng minh G trùng G' hay \(\overrightarrow {GG'} = \overrightarrow 0.\)
Hướng dẫn giải:
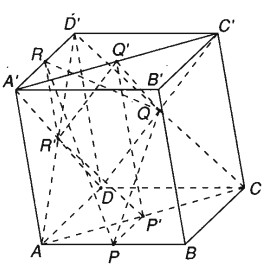
a) Ta có:
\(\overrightarrow {PP'} = {1 \over 2}\overrightarrow {A{\rm{D}}},\overrightarrow {QQ'} = {1 \over 2}\overrightarrow {DA'}, \overrightarrow {R{\rm{R}}'} = {1 \over 2}\overrightarrow {A'A}\)
Vậy:
\(\overrightarrow {PP'} + \overrightarrow {QQ'} + \overrightarrow {R{\rm{R}}'} = {1 \over 2}\left( {\overrightarrow {A{\rm{D}}} + \overrightarrow {DA'} + \overrightarrow {A'A} } \right) = \overrightarrow 0\)
b) Gọi G và G’ lần lượt là trọng tâm các tam giác PQR và P’Q’R’.
Theo câu a) ta có: \(\overrightarrow {PP'} + \overrightarrow {QQ'} + \overrightarrow {R{\rm{R}}'} = \overrightarrow 0\)
Do đó:
\( \left( {\overrightarrow {PG} + \overrightarrow {GG'} + \overrightarrow {G'P'} } \right) + \left( {\overrightarrow {QG} + \overrightarrow {GG'} + \overrightarrow {G'Q'} } \right) + \left( {\overrightarrow {RG} + \overrightarrow {GG'} + \overrightarrow {G'R'} } \right) = \overrightarrow 0 \\ \Leftrightarrow \underbrace {\left( {\overrightarrow {PG} + \overrightarrow {QG} + \overrightarrow {RG} } \right)}_{\overrightarrow 0 } + 3\overrightarrow {GG'} + \underbrace {\left( {\overrightarrow {G'P'} + \overrightarrow {G'Q'} + \overrightarrow {G'R'} } \right)}_{\overrightarrow 0 } = \overrightarrow 0 \)
\( 3\overrightarrow {GG'} = \overrightarrow 0 \) ⟹ G trùng với G’
Vậy hai tam giác PQR và P’Q’R’ có cùng trọng tâm.
Tham khảo thêm
- doc Giải bài tập SBT Toán 11 Bài 2: Hai đường thẳng vuông góc
- doc Giải bài tập SBT Toán 11 Bài 3: Đường thẳng vuông góc với mặt phẳng
- doc Giải bài tập SBT Toán 11 Bài 4: Hai mặt phẳng vuông góc
- doc Giải bài tập SBT Toán 11 Bài 5: Khoảng cách
- doc Giải bài tập SBT Hình học 11 Ôn tập chương 3: Vectơ trong không gian. Quan hệ vuông góc trong không gian
