Giải bài tập SBT Hình học 11 Ôn tập chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
Để các em học sinh lớp 11 có thêm thật nhiều tài liệu ôn tập môn Toán, đội ngũ eLib đã biên soạn và tổng hợp nội dung giải bài tập bài Ôn tập chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song SBT trang 81 - 87 bên dưới đây. Tài liệu gồm các bài tập có phương pháp và đáp án chi tiết đi kèm sẽ giúp các em vừa làm bài vừa đối chiếu đáp án từ đó có kế hoạch học tập phù hợp cho bản thân.
Mục lục nội dung
1.1. Giải bài 2.37 trang 81 SBT Hình học 11
1.2. Giải bài 2.38 trang 81 SBT Hình học 11
1.3. Giải bài 2.39 trang 81 SBT Hình học 11
1.4. Giải bài 2.40 trang 81 SBT Hình học 11
1.5. Giải bài 2.41 trang 82 SBT Hình học 11
1.6. Giải bài 2.42 trang 82 SBT Hình học 11
1.7. Giải bài 2.43 trang 82 SBT Hình học 11
1.8. Giải bài 2.44 trang 82 SBT Hình học 11
2.1. Giải bài 2.45 trang 83 SBT Hình học 11
2.2. Giải bài 2.46 trang 83 SBT Hình học 11
2.3. Giải bài 2.47 trang 83 SBT Hình học 11
2.4. Giải bài 2.48 trang 83 SBT Hình học 11
2.5. Giải bài 2.49 trang 83 SBT Hình học 11
2.6. Giải bài 2.50 trang 84 SBT Hình học 11
3.1. Giải bài 2.51 trang 84 SBT Hình học 11
3.2. Giải bài 2.52 trang 84 SBT Hình học 11
3.3. Giải bài 2.53 trang 84 SBT Hình học 11
3.4. Giải bài 2.54 trang 84 SBT Hình học 11
3.5. Giải bài 2.55 trang 84 SBT Hình học 11
3.6. Giải bài 2.56 trang 85 SBT Hình học 11
3.7. Giải bài 2.57 trang 85 SBT Hình học 11
3.8. Giải bài 2.58 trang 85 SBT Hình học 11
3.9. Giải bài 2.59 trang 86 SBT Hình học 11
3.10. Giải bài 2.60 trang 85 SBT Hình học 11
3.11. Giải bài 2.61 trang 86 SBT Hình học 11
3.12. Giải bài 2.62 trang 86 SBT Hình học 11
3.13. Giải bài 2.63 trang 86 SBT Hình học 11
3.14. Giải bài 2.64 trang 86 SBT Hình học 11
3.15. Giải bài 2.65 trang 86 SBT Hình học 11
3.16. Giải bài 2.66 trang 86 SBT Hình học 11
3.17. Giải bài 2.67 trang 87 SBT Hình học 11
3.18. Giải bài 2.68 trang 87 SBT Hình học 11

1. Câu hỏi và bài tập
1.1. Giải bài 2.37 trang 81 SBT Hình học 11
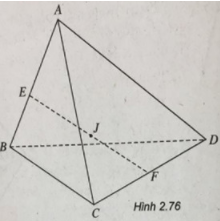
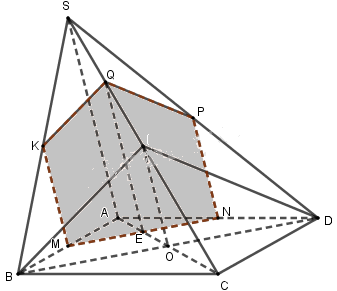
Trong mặt phẳng \(\left( \alpha \right)\) cho tam giác ABC. Từ ba đỉnh của tam giác này ta kẻ các nửa đường thẳng song song cùng chiều Ax, By, Cz không nằm trong \(\left( \alpha \right)\). Trên Ax lấy đoạn AA’ = a, trên By lấy đoạn BB’ = b, trên Cz lấy đoạn CC’ = c.
a) Gọi I, J và K lần lượt là các giao điểm B’C’, C’A’ và A’B’ với \(\left( \alpha \right)\). Chứng minh rằng \(\dfrac{IB}{IC}.\dfrac{JC}{JA}.\dfrac{KA}{KB} = 1\)
b) Gọi G và G’ lần lượt là trọng tâm của các tam giác ABC và A’B’C’. Chứng minh: GG' // AA'.
c) Tính GG’ theo a, b, c.
Phương pháp giải:
a) Sử dụng tính chất của hai tam giác đồng dạng.
b) Áp dụng:
- Tính chất đường trung bình của tam giác.
- Tính chất của trong tâm trong tam giác.
- Định lý Talet.
c) - Chia đoạn GG' thành hai đoạn thuộc hai tam giác.
- Sử dụng định lý Talet để tính từng cạnh đó.
Hướng dẫn giải:
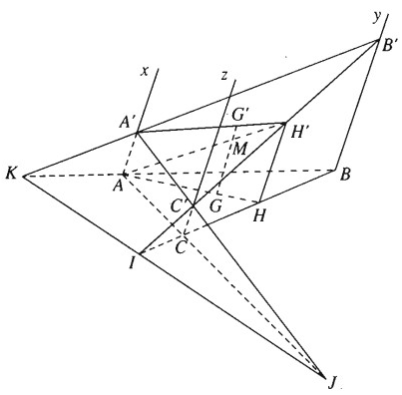
a) Ta có:
\( CC' // BB' \Rightarrow \Delta ICC' \sim \Delta IBB' \\ \Rightarrow \dfrac{IB}{IC}= \dfrac{BB'}{CC'} = \dfrac{b}{c} \\ CC' // AA' \Rightarrow \Delta JCC' \sim \Delta JAA' \\ \Rightarrow \dfrac{JC}{JA}= \dfrac{CC'}{AA'} = \dfrac{c}{a} \\ AA' // BB' \Rightarrow \Delta KAA' \sim \Delta KBB' \\ \Rightarrow \dfrac{KA}{KB}= \dfrac{AA'}{BB'} = \dfrac{a }{ b}\)
Do đó: \(\dfrac{IB}{IC}.\dfrac{JC}{JA}.\dfrac{KA}{KB} = \dfrac{b }{c}.\dfrac{c}{a}.\dfrac{a}{b} = 1\)
b) Gọi H và H’ lần lượt là trung điểm của các cạnh BC và B’C’.
Vì HH’ là đường trung bình của hình thang BB’CC’ nên HH' // BB'.
Mà BB' // AA' suy ra HH' // AA'
Ta có: \(G \in AH\) và \(G' \in A'H'\) và ta có:
\( \left\{ \matrix{ \dfrac{AG}{AH} = \dfrac{2}{3} \hfill \cr \dfrac{A'G'}{A'H'}= \dfrac{2}{3} \hfill \cr} \right. \Rightarrow AA' // GG' // HH'\)
c) Ta có:
\(AH' \cap GG' = M \Rightarrow GG' = G'M + MG\)
Ta có: \(G'M // AA' \Rightarrow \Delta H'G'M \sim \Delta H'A'A\)
\( \Rightarrow \dfrac{G'M}{AA'} = \dfrac{H'G'}{H'A'} = \dfrac{1}{3} \\ \Rightarrow G'M = \dfrac{1}{3}AA' = \dfrac{1}{3}a \\ MG // HH' \Rightarrow \Delta AMG \sim \Delta AH'H \\ \Rightarrow \dfrac{MG}{HH'} =\dfrac{AG}{AH} = \dfrac{2}{3} \\ \Rightarrow MG =\dfrac{2}{3}HH'\)
Mặt khác HH’ là đường trung bình của hình thang BB’CC’ nên
\( HH' = \dfrac{BB' + CC'}{2} = \dfrac{b + c}{2} \\ \Rightarrow MG = \dfrac{2}{3}HH' = \dfrac{2}{3}.\dfrac{b + c}{2} = \dfrac{1}{3}\left( {b + c} \right)\)
Do đó: GG' = G'M + MG
\( = \dfrac{1}{3}a + \dfrac{1}{3}\left( {b + c} \right) \\ = \dfrac{1}{3}\left( {a + b + c} \right)\)
Vậy \(GG' = \dfrac{1}{3}\left( {a + b + c} \right).\)
1.2. Giải bài 2.38 trang 81 SBT Hình học 11
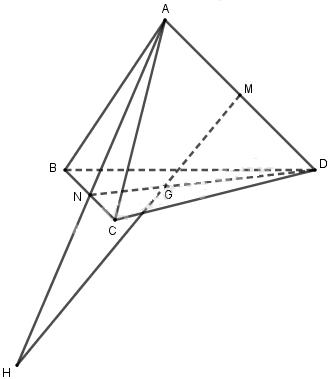
Cho tứ diện ABCD và điểm M nằm trong tam giác BCD.
a) Dựng đường thẳng qua M song song với hai mặt phẳng (ABC) và (ABD). Giả sử đường thẳng này cắt mặt phẳng (ACD) tại B’. Chứng minh rằng AB’, BM và CD đồng quy tại một điểm.
b) Chứng minh \(\dfrac{MB'}{BA}= \dfrac{dt\left( {\Delta MC{\rm{D}}} \right)}{dt\left( {\Delta BC{\rm{D}}} \right)}.\)
c) Đường thẳng song song với hai mặt phẳng (ACB) và (ACD) kẻ từ M cắt (ABD) tại C’ và đường thẳng song song với hai mặt phẳng (ADC) và ADB) kẻ từ M cắt (ABC) tại D’. Chứng minh rằng \(\dfrac{MB'}{BA} + \dfrac{MC'}{CA} + \dfrac{M{\rm{D}}'}{DA} = 1.\)
Phương pháp giải:
a) Gọi I là giao điêm của AB' và BM. Chứng minh I thuộc CD.
b) Áp dụng định lí Talet cho các đường thẳng song song.
c) Áp dụng kết quả câu b với MC' và CA → đpcm.
Hướng dẫn giải:
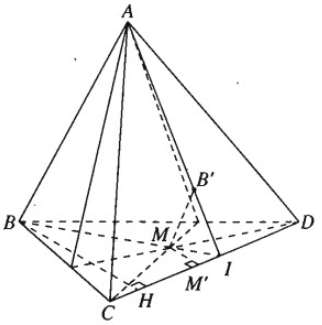
a) Ta có:
\( \left\{ \begin{array}{l}MB' // (ABC )\\MB' // (ABD)\ ABC) \cap (ABD)=AB\end{array} \right. \Rightarrow MB' // AB\)
Do MB' // AB nên MB’ và AB xác định một mặt phẳng.
Gọi \(MB\cup AB’\equiv I.\)
Khi đó \(I \in BM \Rightarrow I \in \left( {BCD} \right)\)
\( I \in AB' \Rightarrow I \in \left( {ACD} \right)\)
Nên \(I \in \left( {BCD} \right) \cap \left( {ACD} \right) = CD, I \in CD\)
Vậy ba đường thẳng AB’, BM và CD đồng quy tại I.
b) \(MB' // AB \Rightarrow \dfrac{MB'}{AB} = \dfrac{IM} {IB}\)
Kẻ \(MM' \bot CD\) và \(BH \bot CD\)
Ta có: \(MM' // BH \Rightarrow \dfrac{IM}{IB} = \dfrac{MM'}{BH}\)
Mặt khác:
\( \left\{ \begin{array}{l}dt(\Delta MCD)=\dfrac{1}{2}CD.MM'\\dt(\Delta BCD)=\dfrac{1}{2}CD.BH\end{array} \right. \\ \Rightarrow\dfrac {dt(\Delta MCD)}{dt(\Delta BCD)}=\dfrac{\dfrac{1}{2}CD.MM'}{\dfrac{1}{2}CD.BH} =\dfrac{MM'}{BH}\)
Do đó:
\(\dfrac{MB'} {AB} = \dfrac{IM}{IB} = \dfrac{MM'}{BH}= \dfrac {dt(\Delta MCD)}{dt(\Delta BCD)}.\)
Vậy \(\dfrac{MB'}{AB} =\dfrac {dt(\Delta MCD)}{dt(\Delta BCD)}.\)
c) Tương tự ta có:
\( \dfrac{MC'}{CA} =\dfrac {dt(\Delta MBD)}{dt(\Delta BCD)} \dfrac{MD'}{DA} =\dfrac {dt(\Delta MBC)}{dt(\Delta BCD)}\)
Vậy:
\( \dfrac{MB'}{BA} + \dfrac{MC'}{CA} + \dfrac{M{\rm{D}}'}{DA} \\ =\dfrac {dt(\Delta MCD)}{dt(\Delta BCD)}+\dfrac {dt(\Delta MBD)}{dt(\Delta BCD)}+\dfrac {dt(\Delta MBC)}{dt(\Delta BCD)} \\ =\dfrac{dt(\Delta MCD)+dt(\Delta MBD)+dt(\Delta MBC)}{dt(\Delta BCD)} =1.\)
1.3. Giải bài 2.39 trang 81 SBT Hình học 11
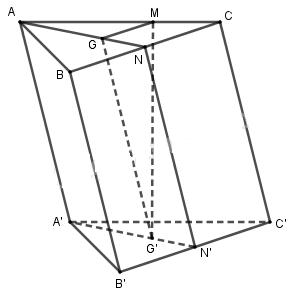
Từ các đỉnh của tam giác ABC ta kẻ các đoạn thẳng AA’, BB’, CC’ song song, cùng chiều, bằng nhau và không nằm trong mặt phẳng của tam giác. Gọi I, G và K lần lượt là trọng tâm của các tam giác ABC, ACC’, A’B’C’.
a) Chứng minh (IGK) // (BB'CC').
b) Chứng minh rằng (A'GK) // (AIB').
Phương pháp giải:
- Để chứng minh hai mặt phẳng song song ta chứng minh mặt phẳng này chứa hai đường thẳng cắt nhau cùng song song với mặt phẳng kia.
- Bài toán sử dụng tính chất của trọng tâm, định lý Talet.
Hướng dẫn giải:
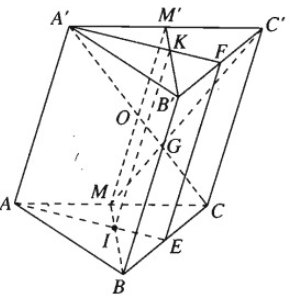
a) Gọi E, F, M lần lượt là trung điểm của là trung điểm của BC, B'C', CC'.
I là trọng tâm của tam giác ABC
\( \Rightarrow \dfrac{AI}{AE}=\dfrac{2}{3}.\)
G là trọng tâm của tam giác ACC'
\( \Rightarrow \dfrac{AG}{AM}=\dfrac{2}{3}.\)
Từ đó suy ra \(\dfrac{AI}{AE}=\dfrac{AG}{AM}=\dfrac{2}{3}.\)
\( \Rightarrow IG // EM \) mà \( EM\subset (BB'C'C) \Rightarrow IG // (BB'C'C)\text{ (1)}\)
K là trọng tâm của tam giác (A'B'C') khi đó \(\dfrac{A'K}{A'F}=\dfrac{2}{3}.\)
Từ đó suy ra \(\dfrac{AI}{AE}=\dfrac{AK}{AF}=\dfrac{2}{3}.\)
⇒IK // AA' mà AA' // BB'
⇒ IK // BB' mà \(BB'\subset (BB'C'C)\)
⇒ IK // (BB'C'C) (2)
Mà \(IG, IK\subset(IGK)\text{ (3)}\)
Từ (1), (2) và (3) suy ra (IGK) // (BB'C'C).
b) Do \( E\in AI, AI\subset (AIB')\)
\( \Rightarrow E\in (AIB') \\ C\in A'G, A'G\subset (A'GK) \\ \Rightarrow C\in (A'GK)\)
Ta có B'E // FC (do tứ giác B'FCG là hình bình hành).
Khi đó B'E // (A'GK) (1)
AI // A'K (do tứ giác A'FEA là hình bình hành).
Khi đó AI // (A'GK) (2)
Mà B'E và AI \(\subset (AIB') \text{(3)}\)
Từ (1), (2) và (3) suy ra (A'GK) // (AIB').
1.4. Giải bài 2.40 trang 81 SBT Hình học 11
Cho hình hộp ABCD.A’B’C’D’. Gọi M và N lần lượt là trung điểm của hai cạnh bên AA’ và CC’. Một điểm P nằm trên cạnh bên DD’.
a) Xác định giao điểm Q của đường thẳng BB’ với mặt phẳng (MNP).
b) Mặt phẳng (MNP) cắt hình hộp theo một thiết diện. Thiết diện đó có tính chất gì?
c) Tìm giao tuyến của mặt phẳng (MNP) với mặt phẳng (ABCD) của hình hộp.
Phương pháp giải:
a) Tìm trong (MNP) đường thẳng cắt BB'. Khi đó Q là giao điểm của đường thẳng đó với BB'.
b) - Tìm giao tuyến của (MNP) với các mặt của hình hộp.
- Thiết diện cần tìm là hình tạo bởi các giao tuyến đó.
- Chứng minh thiết diện có 2 cặp cạnh đối song song.
c) Xét hai trường hợp P không là trung điểm của DD' và P là trung điểm của DD'.
Hướng dẫn giải:
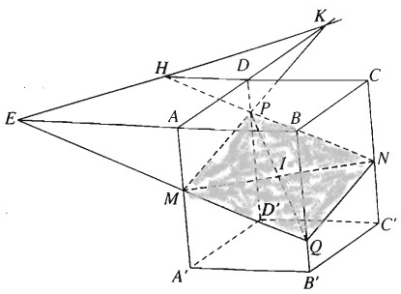
a) Ta có (AA’, DD’) // (BB’, CC’)
\( (MNP)\cap (AA’, DD’)=MP\)
Suy ra giao tuyến của (MNP) và (BB’, CC’) song song với MP.
Ta có \(N\in (MNP)\cap (BB',CC')\)
\( \Rightarrow (MNP)\cap (BB',CC')=Nx\)
Nx // MP.
\( \Rightarrow (MNP)\cap (BB',CC') =Nx\cap BB'=Q\)
b) Ta có
\( (MNP)\cap AA', BB', CC', DD'\) lần lượt tại M, P, N, Q.
⇒ (MNP) cắt hình hộp theo thiết diện MPNQ.
Ta có
\( \left\{ \begin{array}{l} (AA’, BB’) // (DD’, CC’)\\ (MNP)\cap (AA’, BB’)=MQ\\ (MNP)\cap (DD’, CC’)=PN\end{array} \right. \\ \Rightarrow MQ // PN\)
Mà theo câu a) MP // NQ
⇒ Tứ giác MQNP là hình bình hành.
Vậy (MNP) cắt hình hộp theo thiết diện MPNQ là hình bình hành.
c) - TH1: P không phải là trung điểm của DD'
Gọi \(H = PN \cap DC,K = MP \cap AD\).
Ta có d = HK là giao tuyến của mặt phẳng (MNP) với mặt phẳng (ABCD) của hình hộp.
- TH2: P là trung điểm của DD'
Khi đó MP // AD, \(AD\subset (ABCD)\)
\( \Rightarrow MP // (ABCD)\)
Và PN // DC, \(DC\subset (ABCD)\)
\( \Rightarrow PN // (ABCD)\)
Mà MP, \(PN\subset (MNP)\)
⇒ (MNP) // (ABCD) khi đó hai mặt phẳng không có giao tuyến.
1.5. Giải bài 2.41 trang 82 SBT Hình học 11
Cho hình hộp ABCD.A’B’C’D’. Hai điểm M và N lần lượt nằm trên hai cạnh AD và CC’ sao cho \(\dfrac{AM}{MD} = \dfrac{CN}{NC'}.\)
a) Chứng minh rằng đường thẳng MN song song với mặt phẳng (ACB’)
b) Xác định thiết diện của hình hộp cắt bởi mặt phẳng đi qua MN và song song với mặt phẳng (ACB’)
Phương pháp giải:
a) - Chứng minh MN thuộc mặt phẳng song song với (ACB').
b) - Xác định giao tuyến của (P) với các mặt của hình chóp.
- Thiết diện cần tìm là hình tạo bởi các giao tuyến
Hướng dẫn giải:
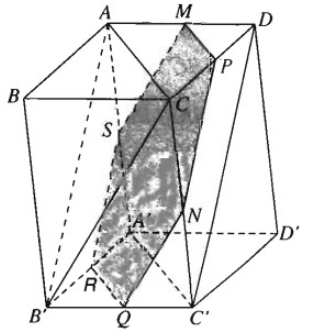
a) Vẽ MP song song với AC và cắt CD tại P
Trong tam giác ADC có: \(\dfrac{AM} {MD} = \dfrac{CP}{PD}\)
Mà \(\dfrac{AM}{MD} = \dfrac{CN}{NC'}.\)
\( \Rightarrow \dfrac{AM} {MD} = \dfrac{CP}{PD}=\dfrac{CN}{NC'}\)
Do đó PN // DC' // AB'
Đường thẳng MN thuộc mặt phẳng (MNP) và mặt phẳng này có MP // AC và PN // AB'.
Vậy mặt phẳng (MNP) song song với mặt phẳng (ACB’) và do đó MN // (ACB')
b) Ta có (MNP) // (ACB’) nên hai mặt phẳng đó cắt các mặt bên của hình hộp theo các giao tuyến song song.
Ta vẽ NQ // CB',QR // C'A' // CA
RS // AB' //PN, SM // QN.
Thiết diện của hình hộp cắt bởi mặt phẳng đi qua MN và song song với mặt phẳng (ACB’) là hình lục giác MPNQRS có các cạnh đối diện song song với nhau từng đôi một: MP // RQ,PN // SR,NQ // MS.
1.6. Giải bài 2.42 trang 82 SBT Hình học 11
Cho hình lăng trụ tứ giác ABCD.A’B’C’D’.
a) Chứng minh rằng hai đường chéo AC’ và A’C cắt nhau và hai đường chéo BD’ và B’D cắt nhau.
b) Cho E và F lần lượt là trung điểm của hai đường chéo AC và BD.Chứng minh MN = EF.
Phương pháp giải:
a) Nhận xét tính chất của các tứ giác ACC'A' và BDD'B'.
b) Sử dụng tính chất đường trung bình của tam giác và suy ra đpcm.
Hướng dẫn giải:
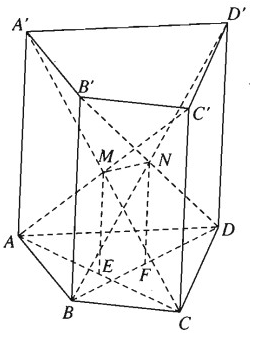
a) Hình bình hành ACC’A' có hai đường chéo là AC’ và A’C cắt nhau tại trung điểm M của mỗi đường.
Tương tự, hai đường chéo BD’ và B’D cắt nhau tại trung điểm N của mỗi đường.
b) Trung điểm E của AC là hình chiếu của trung điểm M của AC’ theo phương của cạnh lăng trụ.
Tương tự, trung điểm F là hình chiếu trung điểm N của đường chéo BD’ trên BD.
Ta có EM // CC' và \(EM = {{CC'} \over 2}\)
Mặt khác FN // DD' và \(FN = {{DD'} \over 2}.\)
Từ đó suy ra tứ giác MNFE là hình bình hành và ta có MN = EF.
1.7. Giải bài 2.43 trang 82 SBT Hình học 11
Cho hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) cắt nhau theo giao tuyến m. Trên đường thẳng d cắt \(\left( \alpha \right)\) ở A và cắt \(\left( \beta \right)\) ở B ta lấy hai diểm cố định S1, S2 không thuộc \(\left( \alpha \right)\), \(\left( \beta \right)\). Gọi M là một điểm di động trên \(\left( \beta \right)\). Giả sử các đường thẳng \(M{S_1},M{S_2}\) cắt \(\left( \alpha \right)\) lần lượt tại M1 và M2.
a) Chứng minh rằng M1M2 luôn luôn đi qua một điểm cố định.
b) Giả sử đường thẳng M1M2 cắt giao tuyến m tại K. Chứng minh rằng ba điểm K, B, M thẳng hàng.
c) Gọi b là một đường thẳng thuộc mặt phẳng \(\left( \beta \right)\) nhưng không đi qua điểm B và cắt m tại I. Chứng minh rằng khi M di động trên b thì các điểm M1 và M2 di động trên hai đường thẳng cố định thuộc mặt phẳng \(\left( \alpha \right)\).
Phương pháp giải:
a) Chứng minh M1M2 đi qua A cố định.
b) Chứng minh K thuộc giao tuyến của (M,d) và \((\beta )\).
c) Chứng minh các điểm M1 và M2 chạy trên các giao tuyến của hai mặt phẳng cố định.
Hướng dẫn giải:
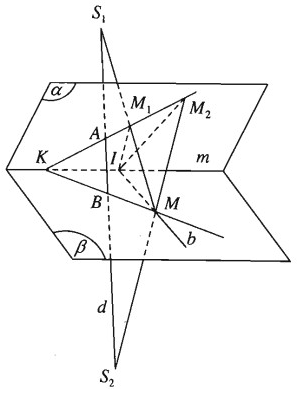
a) Mặt phẳng (M, d) cắt \(\left( \alpha \right)\) theo giao tuyến M1M2.
Điểm A cũng thuộc giao tuyến đó.
Vậy đường thẳng M1M2 luôn luôn đi qua điểm A cố định.
b) Mặt phẳng (M, d) cắt \(\left( \beta \right) \) theo giao tuyến BM.
Điểm K thuộc giao tuyến đó nên ba điểm K, B, M thẳng hàng.
c) Giả sử b cắt m tại I thì mặt phẳng (S1, b) luôn luôn cắt \(\left( \alpha \right)\) theo giao tuyến IM1.
Do đó điểm M1 di động trên giao tuyến của IM1 cố định.
Còn khi M di động trên b thì mặt phẳng (S2, b) cắt \(\left( \alpha \right)\) theo giao tuyến IM2.
Do đó điểm M2 chạy trên giao tuyến IM2 cố định.
1.8. Giải bài 2.44 trang 82 SBT Hình học 11
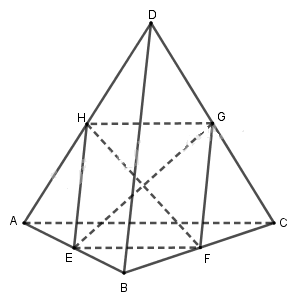
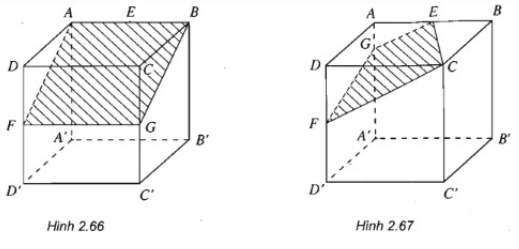
Cho hình lập phương ABCD.A’B’C’D’ các trung điểm E, F của các cạnh AB, DD’. Hãy xác định các thiết diện của hình lập phương cắt bởi các mặt phẳng (EFB), (EFC), (EFC’) và (EFK) với K là trung điểm của cạnh B’C’.
Phương pháp giải:
- Xác định giao tuyến (nếu có) của các mặt phẳng đã cho với các mặt của hình lập phương.
- Từ đó suy ra thiết diện cần tìm.
Hướng dẫn giải:
Ta xác định thiết diện của hình lập phương cắt bởi các mặt phẳng sau:
- Mặt phẳng (EFB): ta vẽ FG // AB và được thiết diện là hình chữ nhật ABGF, G là trung điểm của CC’.
- Mặt phẳng (EFC): Nối FC và vẽ EG // FC, ta được thiết diện là hình thang \(ECFG\left( {AG = {1 \over 4}AA'} \right).\)
- Mặt phẳng (EFC’): Nối FC’ và vẽ EG // FC'. Nối GC’ và vẽ FH // GC'. Ta được thiết diện là hình ngũ giác EGC’FH.
\( \left( {BG = {1 \over 4}BB',AH = {1 \over 3}A{\rm{D}}} \right)\)
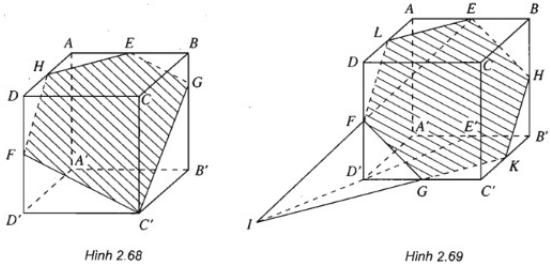
- Mặt phẳng (EFK) với K là trung điểm của đoạn B’C’.
Lấy trung điểm E’ của đoạn A’B’. Ta có \(I = EF \cap E'D'.\)
Ta có IK là giao tuyến của hai mặt phẳng (EFK) và (A’B’C’D’).
Gọi \(G = IK \cap C'D'\). Nối F với G, vẽ EH // FG.
Nối K với H, vẽ FL // KH và nối L với E.
Ta được thiết diện là hình lục giác đều EHKGFL. (G, H, L theo thứ tự là trung điểm của D’C’, B’B, AD).
2. Bài tập tổng hợp
2.1. Giải bài 2.45 trang 83 SBT Hình học 11
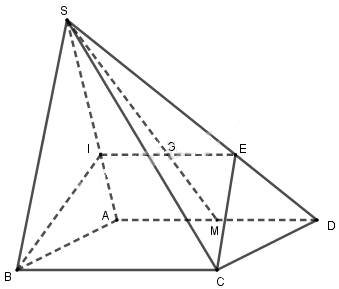
Cho hình chóp S.ABCD có đáy là hình thang (đáy lớn AD ). Gọi O là giao điểm của AC và BD, I và J lần lượt là trung điểm của SB và SC.
a) Xác định giao điểm M của AI và (SCD).
b) Chứng minh IJ // (SAD).
c) Xác định thiết diện của hình chóp cắt bởi mp (P) qua I, song song với SD và AC.
Phương pháp giải:
a) Mở rộng mặt phẳng (SCD), từ đó tìm giao điểm M.
b) Chứng minh IJ song song với một đường thẳng nằm trong (SAD).
c) Xác định giao tuyến của (P) với các mặt của hình chóp.
Hướng dẫn giải:
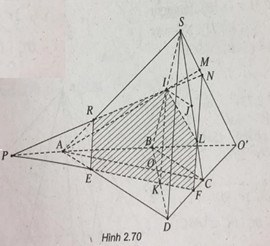
a) Gọi \(O' = AB \cap C{\rm{D}},M = AI \cap SO'\)
Ta có: \(M = AI \cap \left( {SC{\rm{D}}} \right)\)
b)
Ta có:
\( \eqalign{ & IJ // BC \Rightarrow IJ // AD \cr & \Rightarrow IJ // \left( {SAD} \right) \cr}\)
c) Đường thẳng qua I song song với SD cắt BD tại K.
Do \({{OB} \over {O{\rm{D}}}} = {{BC} \over {A{\rm{D}}}} < 1\) nên OB < OD.
Do đó điểm K thuộc đoạn OD.
Qua K, kẻ đường thẳng song song với AC cắt DA, DC, BA lần lượt tại E, F, P.
Gọi \(R = IP \cap SA\). Kéo dài PI cắt SO’ tại N
Gọi \(L = NF \cap SC\)
Ta có thiết diện là ngũ giác IREFL.
2.2. Giải bài 2.46 trang 83 SBT Hình học 11
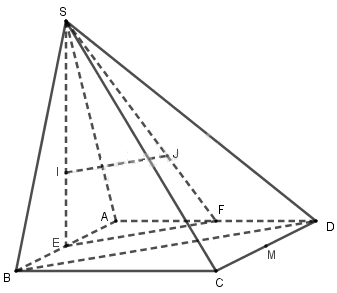
Cho hình chóp S.ABCD, có đáy là hình bình hành. Gọi C’ là trung điểm của SC và M là một điểm di động trên cạnh SA. Mặt phẳng (P) di động luôn đi qua C’M và song song với BC.
a) Xác định thiết diện (P) cắt hình chóp S.ABCD. Xác định vị trí điểm M để thiết diện là hình bình hành.
b) Khi M di động trên cạnh SA, thì giao điểm của hai cạnh đối của thiết diện chạy trên đường nào?
Phương pháp giải:
a) - Xác định giao tuyến (nếu có) của các mặt phẳng đã cho với các mặt của hình lập phương.
- Từ đó suy ra thiết diện cần tìm.
b) Tìm giao tuyến của hai mặt phẳng mà điểm có thể chạy trên đó.
Hướng dẫn giải:
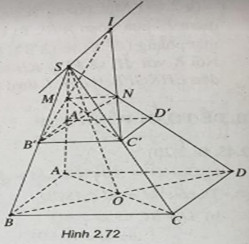
a) (P) // BC nên (P) sẽ cắt (SBC) theo giao tuyến B’C’ song song với BC.
Tương tự, (P) cắt (SAD) theo giao tuyến MN song song với AD.
Khi M trùng với trung điểm A’ của cạnh SA thì thiết diện MB’C’N’ là hình bình hành.
b) Với M không trùng với A’:
Gọi \(I \in B'M \cap C'N\). Ta có:
\( I \in B'M \subset \left( {SAB} \right)\), tương tự \(I' \in C'N \subset \left( {SC{\rm{D}}} \right)\)
Như vậy \(I \in \Delta = \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right).\)
2.3. Giải bài 2.47 trang 83 SBT Hình học 11
Cho hình chóp S.ABCD có đáy là hình thang ABCD (có đáy nhỏ BC ). Gọi M, N lần lượt là trung điểm của AB và SD, O là giao điểm của AC và DM.
a) Tìm giao điểm của MN và mặt phẳng (SAC).
b) Tìm thiết diện của hình chóp với mặt phẳng (NBC). Thiết diện đó là hình gì?
Phương pháp giải:
a) - Tìm mặt phẳng chứa MN và cắt (SAC).
- Tìm giao tuyến của (SAC) với mặt phẳng vừa tìm.
- Tìm giao điểm của MN với giao tuyến trên và kết luận.
b) - Tìm giao tuyến của (NBC) với các mặt của hình chóp (nếu có).
- Từ đó suy ra thiết diện cần tìm.
Hướng dẫn giải:
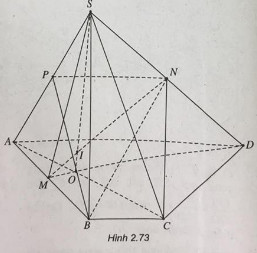
a) Gọi \(O = AC \cap MD\). Trong mặt phẳng (SMB) gọi \(I = SO \cap MN.\)
Ta có: \(I = \left( {SAC} \right) \cap MN\)
b) Ta có:
\(A{\rm{D}} // BC\left( {BC \subset \left( {SBC} \right)} \right) \Rightarrow A{\rm{D}} // \left( {SBC} \right).\)
Mặt phẳng (SAD) cắt mặt phẳng (NBC) theo giao tuyến \(NP // A{\rm{D}}\left( {P \in SA} \right).\)
Ta có thiết diện cần tìm là hình thang BCNP.
2.4. Giải bài 2.48 trang 83 SBT Hình học 11
Cho hình chóp S.ABCD có đáy là tứ giác ABCD. Gọi G1 và G2 lần lượt là trọng tâm của các tam giác SBC và SCD
Tìm giao tuyến của mặt phẳng \((AG_1G_2)\) với các mặt phẳng (ABCD) và (SCD).
Xác định thiết diện của hình chóp với mặt phẳng \((AG_1G_2).\)
Phương pháp giải:
- Sử dụng tính chất: "Nếu mặt phẳng (P) song song với đường thẳng a nằm trong mặt phẳng (Q) thì (P) cắt (Q) theo giao tuyến b // a ".
- Tìm các giao tuyến của \((AG_1G_2)\) với các mặt của hình chóp suy ra thiết diện.
Hướng dẫn giải:
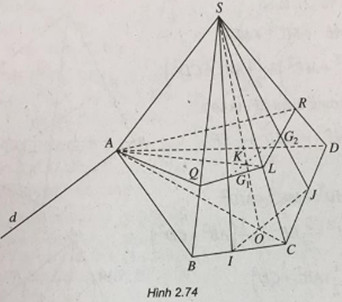
Gọi I, J lần lượt là trung điểm của BC, CD.
Ta có \(IJ // {G_1}{G_2}\) nên giao tuyến của hai mặt phẳng \((AG_1G_2)\) và (ABCD) là đường thẳng d qua A và song song với IJ
Gọi \(O = IJ \cap AC, K = {G_1}{G_2} \cap SO,L = AK \cap SC\)
LG2 cắt SD tại R
LG2 cắt SB tại Q
Khi đó \(\left( {A{G_1}{G_2}} \right) \cap \left( {SCD} \right) = LR\)
Ta có thiết diện là tứ giác AQLR.
2.5. Giải bài 2.49 trang 83 SBT Hình học 11
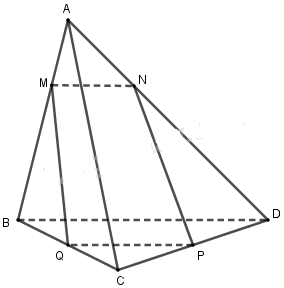
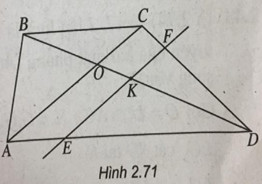
Cho tứ diện ABCD. Trên ba cạnh AB, AC, AD lần lượt lấy các điểm B’, C’, D’ sao cho đường thẳng B’C’ cắt đường thẳng BC tại K, đường thẳng C’D’ cắt đường thẳng CD tại J, đường thẳng D’B’ cắt đường thẳng DB tại I.
a) Chứng minh ba điểm I, J, K thẳng hàng.
b) Lấy điểm M ở giữa đoạn thẳng BD ; điểm N ở giữa đoạn thẳng CD sao cho đường thẳng MN cắt đường thẳng BC và điểm F nằm bên trong tam giác ABC. Xác định thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MNF).
Phương pháp giải:
a) Chứng minh ba điểm I, J, K cùng thuộc giao tuyến của (CBD) và (C’B’D’).
b) - Xác định giao tuyến của mặt phẳng (MNF) với các mặt của ABCD.
- Từ đó suy ra thiết diện cần tìm.
Hướng dẫn giải:
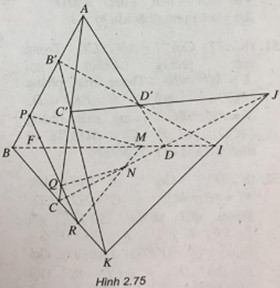
a) Ta có:
\(K = B'C' \cap BC\)\( \Rightarrow \left\{ \begin{array}{l}K \in B'C' \subset \left( {B'C'D'} \right)\\K \in BC \subset \left( {BCD} \right)\end{array} \right.\) \( \Rightarrow K \in \left( {B'C'D'} \right) \cap \left( {BCD} \right)\) \(J = C'D' \cap CD\)\( \Rightarrow \left\{ \begin{array}{l}J \in C'D' \subset \left( {B'C'D'} \right)\\J \in CD \subset \left( {BCD} \right)\end{array} \right.\) \( \Rightarrow J \in \left( {B'C'D'} \right) \cap \left( {BCD} \right)\)
Do đó \(KJ = \left( {B'C'D'} \right) \cap \left( {BCD} \right)\)
Mà
\(I = B'D' \cap BD\)\( \Rightarrow \left\{ \begin{array}{l}I \in B'D' \subset \left( {B'C'D'} \right)\\I \in BD \subset \left( {BCD} \right)\end{array} \right.\) \( \Rightarrow I \in \left( {B'C'D'} \right) \cap \left( {BCD} \right) = KJ\)
Vậy ba điểm I, J, K thẳng hàng.
b) Trong (BCD), gọi \(R = MN \cap BC\)
Trong (ABC), gọi P, Q lần lượt là giao điểm của RF với AB, AC.
Khi đó
\(\begin{array}{l}\left( {MNF} \right) \cap \left( {BCD} \right) = MN\\\left( {MNF} \right) \cap \left( {ACD} \right) = NQ\\\left( {MNF} \right) \cap \left( {ABC} \right) = QP\\\left( {MNF} \right) \cap \left( {ABD} \right) = PM\end{array}\)
Vật thiết diện là tứ giác MNQP.
2.6. Giải bài 2.50 trang 84 SBT Hình học 11
Cho tứ diện ABCD. Tìm vị trí điểm M trong không gian sao cho: \(M{A^2} + M{B^2} + M{C^2} + M{{\rm{D}}^2}\) đạt giá trị cực tiểu.
Phương pháp giải:
Sử dụng tính chất: Cho I là trung điểm đoạn thẳng AB. Với điểm M bất kì ta luôn có:
\( MA^2+MB^2=2MI^2+\dfrac{1}{2}AB^2\)
Hướng dẫn giải:
Gọi E, F lần lượt là trung điểm của AB và CD. Ta có:
\( \displaystyle M{A^2} + M{B^2} = 2M{E^2} + {1 \over 2}A{B^2}\,\,\,\,\,\left( 1 \right) \\ \displaystyle M{C^2} + M{D^2} = 2M{F^2} + {1 \over 2}C{{\rm{D}}^2}\,\,\,\,\,\left( 2 \right)\)
Cộng (1) và (2) ta có:
\( \displaystyle M{A^2} + M{B^2} + M{C^2} + M{{\rm{D}}^2} \\ \displaystyle = 2\left( {M{E^2} + M{F^2}} \right) + {1 \over 2}\left( {A{B^2} + C{{\rm{D}}^2}\,\,} \right)\,\,\)
Gọi J là trung điểm của EF, ta có:
\( \displaystyle \left( {M{E^2} + M{F^2}} \right) = 2M{J^2}\, + {1 \over 2}E{F^2}\)
Khi đó:
\( \displaystyle \eqalign{ & M{A^2} + M{B^2} + M{C^2} + M{{\rm{D}}^2} \cr & = 2\left( {2M{J^2}\, + {1 \over 2}E{F^2}} \right) + {1 \over 2}\left( {A{B^2} + C{{\rm{D}}^2}} \right) \cr & \ge E{F^2} + {1 \over 2}\left( {A{B^2} + C{{\rm{D}}^2}} \right) \cr} \)
Vậy \(\displaystyle M{A^2} + M{B^2} + M{C^2} + M{{\rm{D}}^2}\) đạt giá trị nhỏ nhất khi \(\displaystyle M \equiv J.\)
3. Bài tập trắc nghiệm
3.1. Giải bài 2.51 trang 84 SBT Hình học 11
Khẳng định nào sau đây đúng?
A. Nếu một mặt phẳng cắt một trong hai đường thẳng song song thì mặt phẳng đó sẽ cắt đường thẳng còn lại.
B. Hai mặt phẳng lần lượt đi qua hai đường thẳng song song thì cắt nhau theo một giao tuyến song song với một trong hai đường thẳng đó.
C. Nếu một đường thẳng cắt một trong hai đường thẳng song song thì đường thẳng đó sẽ cắt đường thẳng còn lại.
D. Hai mặt phẳng có một điểm chung thì cắt nhau theo một giao tuyến đi qua điểm chung nào đó.
Phương pháp giải:
Suy luận từng đáp án, cho ví dụ đáp án sai.
Hướng dẫn giải:
Đáp án A: nếu a // b và (α) cắt a thì (α) cắt b nên A đúng.
Đáp án B: sai vì có thể xảy ra hai mp song song.
Đáp án C: sai vì có thể chéo nhau.
Đáp án D: sai vì có thể hai mp đó trùng nhau.
Chọn đáp án: A
3.2. Giải bài 2.52 trang 84 SBT Hình học 11
Khẳng định nào sau đây đúng?
A. Nếu hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất.
B. Hai mặt phẳng có một điểm chung thì chúng còn vô số điểm chung khác nữa.
C. Tồn tại duy nhất một mặt phẳng đi qua 3 điểm phân biệt.
D. Tồn tại duy nhất một mặt phẳng đi qua 1 điểm và một đường thẳng cho trước
Phương pháp giải:
Suy luận từng đáp án, cho ví dụ đáp án sai.
Hướng dẫn giải:
- Khẳng định “ Nếu hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất” là SAI, vì có thể hai mặt phẳng trùng nhau.
- Khẳng định “Tồn tại duy nhất một mặt phẳng đi qua 3 điểm phân biệt” là SAI vì thiếu điều kiện ba điểm không thẳng hàng.
- Khẳng định “Tồn tại duy nhất một mặt phẳng đi qua một điểm và một đường thẳng cho trước” SAI vì thiếu điều kiện điểm không nằm trên đường thẳng.
Chọn đáp án: B
3.3. Giải bài 2.53 trang 84 SBT Hình học 11
Cho a ⊂ (P); b ⊂ (Q). Khẳng định nào sau đây đúng?
A. (P) // (Q) ⇒ a // b
B. a // b ⇒ (P) // (Q)
C. (P) // (Q) ⇒ a // (Q), b // (P)
D. a và b chéo nhau
Phương pháp giải:
Áp dụng định nghĩa: Hai mặt phẳng song song thì không có điểm chung.
Hướng dẫn giải:
Vì hai mặt phẳng song song thì không có điểm chung nên a và (Q) không có điểm chung, b và (P) không có điểm chung hay a // (Q), b // (P).
Chọn đáp án: C
3.4. Giải bài 2.54 trang 84 SBT Hình học 11
Cho đường thẳng a và mặt phẳng (P) song song với nhau. Khi đó, số đường thẳng phân biệt nằm trong (P) và song song với a là
A. 0 B. 2 C. vô số D. 3
Phương pháp giải:
Áp dụng tính chất: “Đường thẳng a và mặt phẳng (P) song song với nhau khi trong mặt phẳng (P) tồn tại đường thẳng b song song với đường thẳng a”.
Hướng dẫn giải:
Ta có qua một điểm bất kì nằm trong mặt phẳng (P) mà không thuộc đường thẳng b ta sẽ kẻ một đường thẳng c song song với b cũng nằm trong mặt phẳng (P)
Do đó đường thẳng vừa kẻ này sẽ song song với đường thẳng a.
Số điểm ở trong mặt phẳng (P) mà không thuộc đường thẳng b là vô số.
Vậy số đường thẳng chứa trong mặt phẳng (P) mà song song với đường thẳng a sẽ là vô số.
Chọn đáp án: C
3.5. Giải bài 2.55 trang 84 SBT Hình học 11
Cho mặt phẳng (R) cắt hai mặt phẳng song song (P) và (Q) theo hai giao tuyến a và b. Khi đó, ta có
A. a và b song song hoặc trùng nhau
B. a và b cắt nhau
C. a và b trùng nhau
D. a và b song song
Phương pháp giải:
Áp dụng tính chất: “Một mặt phẳng thứ ba cắt hai mặt phẳng song song với nhau theo hai giao tuyến song song với nhau.”
Hướng dẫn giải:
Chọn đáp án: D
3.6. Giải bài 2.56 trang 85 SBT Hình học 11
Khẳng định nào sau đây đúng?
A. Hai đường thẳng phân biệt không cắt nhau thì chéo nhau.
B. Hai đường thẳng phân biệt cùng nằm trong một mặt phẳng thì không chéo nhau.
C. Hai đường thẳng không có điểm chung thì song song với nhau.
D. Hai đường thẳng phân biệt lần lượt nằm trong hai mặt phẳng khác nhau thì chéo nhau.
Phương pháp giải:
Suy luận từng đáp án, cho ví dụ đáp án sai.
Hướng dẫn giải:
- Khẳng định “Hai đường thẳng phân biệt không cắt nhau thì chéo nhau” là SAI vì chúng có thể song song với nhau.
- Khẳng định “Hai đường thẳng không có điểm chung thì song song với nhau” là SAI vì chúng có thể chéo nhau.
- Khẳng định “Hai đường thẳng phân biệt lần lượt nằm trong hai mặt phẳng khác nhau thì chéo nhau” là SAI vì có thể hai đường thẳng này cùng thuộc một mặt phẳng thứ ba (nghĩa là chúng có thể song song).
Chọn đáp án: B
3.7. Giải bài 2.57 trang 85 SBT Hình học 11
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AD và BC, G là trọng tâm tam giác BCD. Khi ấy giao điểm của MG và mặt phẳng (ABC) là
A. điểm N.
B. điểm C.
C. Giao điểm của đường thẳng MG và đường thẳng BC.
D. Giao điểm của đường thẳng MG và đường thẳng AN.
Phương pháp giải:
Tìm trong (ABC) một đường thẳng có thể cắt MG.
→ Giao điểm của MG với đường thẳng đó là giao điểm cần tìm.
Hướng dẫn giải:
Ta có: \(AN = \left( {ADN} \right) \cap \left( {ABC} \right)\)
Trong (ADN), MG và AN không song song \((vì \frac{{DM}}{{DA}} = \frac{1}{2} \ne \frac{2}{3} = \frac{{DG}}{{DN}} )\) nên gọi \(H = AN \cap MG\)
Khi đó \(\left\{ \begin{array}{l}H \in AN \subset \left( {ABC} \right)\\H \in MG\end{array} \right. \Rightarrow H = MG \cap \left( {ABC} \right)\)
Vậy giao điểm của MG và mặt phẳng (ABC) là giao điểm của MG với AN.
Chọn đáp án: D
3.8. Giải bài 2.58 trang 85 SBT Hình học 11
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Gọi G là trọng tâm tam giác SAD. Mặt phẳng (GBC) cắt SD tại E. Tỉ số SE / SD là
A. 1 B. 1/2
C. 2/3 D. 3/2
Phương pháp giải:
- Chứng minh SE / SD = SG / SM.
- Áp dụng tính chất trọng tâm để tính tỉ số.
Hướng dẫn giải:
Mặt phẳng (SAD) và (GBC) có G là một điểm chung.
Mặt khác, (SAD) và (GBC) lần lượt chứa hai đường thẳng song song là AD và BC
Nên giao tuyến của chúng là đường thẳng qua G song song với AD.
Giao tuyến này cắt SD tại E. Gọi M là trung điểm AD, ta có GE // MD
\( \Rightarrow \frac{{SE}}{{SD}} = \frac{{SG}}{{SM}} = \frac{2}{3}\)
Chọn đáp án: C
3.9. Giải bài 2.59 trang 85 SBT Hình học 11
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J lần lượt là trọng tâm các tam giác SAB, SAD. Lấy M là trung điểm CD. Khẳng định nào sau đây đúng?
A. IJ // (SBM) B. IJ // (SBD)
C. IJ // (SBC) D. IJ // (SCD)
Phương pháp giải:
- Gọi E, F lần lượt là trung điểm AB, AD.
- Dựa vào định lý Talet chứng minh IJ song song với EF.
Hướng dẫn giải:
Gọi E, F lần lượt là trung điểm AB, AD.
Ta có: \(\frac{{SI}}{{SE}} = \frac{{SJ}}{{SF}} = \frac{2}{3} \) ⇒ IJ // EF.
Mà EF // BD nên IJ // BD.
Do IJ không nằm trên (SBD), ta có: IJ // (SBD).
Chọn đáp án: B
3.10. Giải bài 2.60 trang 85 SBT Hình học 11
Khẳng định nào sau đây đúng?
A. Nếu hai mặt phẳng (α) và (β) song song với nhau thì mọi đường thẳng nằm trong (α) đều song song với (β)
B. Nếu hai mặt phẳng (α) và (β) song song với nhau thì mọi đường thẳng nằm trong (α) đều song song với mọi đường thẳng trong (β)
C. Trong (α) có chứa hai đường thẳng phân biệt và hai đường thẳng này cùng song song với (β) thì (α) và (β) song song với nhau.
D. Qua một điểm nằm ngoài mặt phẳng (α) cho trước ta vẽ được một và chỉ một đường thẳng song song với mặt phẳng cho trước đó.
Phương pháp giải:
Suy luận từng đáp án, cho ví dụ đáp án sai.
Hướng dẫn giải:
- Khẳng định “Nếu hai mặt phẳng (α) và (β) song song với nhai thì mọi đường thẳng nằm trong (α) đều song song với mọi đường thẳng nằm trong (β)” là SAI vì hai đường thẳng có thể chéo nhau.
- Khẳng định “Nếu (α) có chứa hai đường thẳng phân biệt và hai đường thẳng này cùng song song với (β) thì (α) và (β) song song” là SAI vì thiếu điều kiện hai đường thẳng đó cắt nhau.
- Khẳng định “Qua một điểm nằm ngoài mặt phẳng cho trước ta vẽ được một là chỉ một đường thẳng song song với mặt phẳng cho trước đó” là SAI vì vẽ được vô số đường thẳng như vậy.
- Khẳng định “Nếu hai mặt phẳng (α) và (β) song song với nhau thì mọi đường thẳng nằm trong (α) đều song song với (β)” là khẳng định đúng.
Chọn đáp án: A
3.11. Giải bài 2.61 trang 86 SBT Hình học 11
Cho lăng trụ ABC.A'B'C'. Gọi G, G' lần lượt là trọng tâm của tam giác ABC, A'B'C'. M là điểm trên cạnh AC sao cho AM = 2MC. Khẳng định nào sau đây sai?
A. GG' // (ACC'A')
B. GG' // (ABB'A')
C. MG' // (BCC'B') ≠ ∅
D. (MGG') // (BCC'B')
Phương pháp giải:
Chứng minh từng đáp án để tìm câu sai.
Hướng dẫn giải:
Gọi N, N’ là trung điểm của BC, B’C’.
Ta có ANN’A’ là hình bình hành AA’ song song và bằng NN’ nên GG’ // AA’.
Do đó GG’ // (ABB’A’), GG’ // (ACC’A’) nên A, B đều đúng.
Mặt khác: \(\frac{{AG}}{{AN}} = \frac{{AM}}{{AC}} = \frac{2}{3}\) nên GM // CN ⇒ GM // (BCC'B').
Mà GG'// (BCC'B') nên (MGG’) // (BCCB’).
Do vậy khẳng định “Đường thẳng MG’ cắt mặt phẳng (BCC’B’) là khẳng định SAI.
Chọn đáp án: C
3.12. Giải bài 2.62 trang 86 SBT Hình học 11
Cho mặt phẳng (P) và đường thẳng d ⊂ (P). Khẳng định nào sau đây đúng?
A. Nếu 3 điểm A, B, C cùng thuộc (P) và A, B, C thẳng hàng thì A, B, C ∈ d.
B. Nếu A ∉ d thì A ∉ (P).
C. Nếu A ∈ (P) thì A ∉ d.
D. ∀A, A ∈ d ⇒ A ∈ (P)
Phương pháp giải:
Áp dụng tính chất: “Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm nằm trên đường thẳng đó đều nằm trên mặt phẳng đó”.
Hướng dẫn giải:
Khẳng định “Nếu A ∉ d thì A ∉ (P)” là SAI vì có thể vẫn thuộc (P) nhưng không nằm trên d.
Chọn đáp án: D
3.13. Giải bài 2.63 trang 86 SBT Hình học 11
Khẳng định nào sau đây sai?
A. Qua một điểm và một đường thẳng không chứa điểm đó có duy nhất một mặt phẳng.
B. Qua hai đường thẳng cắt nhau có duy nhất một mặt phẳng.
C. Qua hai đường thẳng song song có duy nhất một mặt phẳng.
D. Qua hai đường thẳng không chéo nhau có duy nhất một mặt phẳng.
Phương pháp giải:
Dựa vào các cách xác định mặt phẳng để tìm đáp án sai.
Hướng dẫn giải:
Đáp án A, B, C đúng theo các cách xác định mặt phẳng.
Đáp án D: Nếu hai đường thẳng trùng nhau thì có vô số mặt phẳng nên D sai.
Chọn đáp án: D
3.14. Giải bài 2.64 trang 86 SBT Hình học 11
Cho năm điểm A, B, C, D, E sao cho không có bốn điểm nào cùng nằm trên một mặt phẳng. Số hình tứ diện có các đỉnh lấy từ năm điểm đã cho là
A. 5 B. 6 C. 3 D. 4
Phương pháp giải:
Chọn 4 trong 5 điểm là tổ hợp chập 4 của 5 phần tử.
Hướng dẫn giải:
Lấy bốn điểm trong năm điểm có: C54 = 5 cách (vì bốn điểm trong năm điểm đều tạo thành tứ diện).
Chọn đáp án: A.
3.15. Giải bài 2.65 trang 86 SBT Hình học 11
Cho tứ diện ABCD. Trên các cạnh AB, AD lần lượt lấy các điểm M, N sao cho \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AD}} = \frac{1}{3}\). Gọi P, Q lần lượt là trung điểm các cạnh CD, CB.
Khẳng định nào sau đây đúng?
A. Bốn điểm M, N, P, Q không đồng phẳng.
B. Tứ giác MNPQ là hình bình hành.
C. Tứ giác MNPQ là hình thang.
D. Tứ giác MNPQ không có các cặp cạnh đối nào song song.
Phương pháp giải:
Áp dụng định lý Talet và tính chất đường trung bình suy ra các cạnh song song → hình tính của MNPQ.
Hướng dẫn giải:
Vì \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AD}} = \frac{1}{3}\) nên MN // BD
Tam giác BCD có PQ là đường trung bình nên PQ // BD và PQ = \(\frac{1}{2}\) BD
Do đó MN // PQ và MN < PQ nên tứ giác MNPQ là một hình thang.
Chọn đáp án: D
3.16. Giải bài 2.66 trang 86 SBT Hình học 11
Cho tứ diện đều ABCD. Một mặt phẳng (α) qua trung điểm của cạnh AB và lần lượt song song với AC và BD cắt tứ diện trên theo thiết diện là
A. hình chữ nhật. B. hình vuông.
C. hình thoi. D. hình thang cân.
Phương pháp giải:
- Thiết diện là hình tạo bởi giao tuyến của (α) với các mặt của tứ diện.
- Xác định hình tính của thiết diện và chọn câu đúng.
Hướng dẫn giải:
Gọi E là trung điểm AB. Ta có \(E \in \left( {ABC} \right) \cap \left( \alpha \right).\)
\( \left\{ \begin{array}{l}AC \subset \left( {ABC} \right)\\AC//\left( \alpha \right)\\\left( \alpha \right) \cap \left( {ABC} \right) = Ex\end{array} \right. \Rightarrow Ex//AC\)
Trong mp(ABC), kẻ Ex // AC cắt BC tại F nên F là trung điểm BC.
Ta có:
\(\left\{ \begin{array}{l}F \in \left( \alpha \right) \cap \left( {BCD} \right)\\BD \subset \left( {BCD} \right)\\BD//\left( \alpha \right)\\\left( \alpha \right) \cap \left( {BCD} \right) = Fy\end{array} \right. \Rightarrow Fy//BD\)
Trong mp(BCD), kẻ Fy // BD cắt DC tại G, khi đó G là trung điểm DC.
Ta có:
\(\left\{ \begin{array}{l}G \in \left( \alpha \right) \cap \left( {ACD} \right)\\AC \subset \left( {ACD} \right)\\AC//\left( \alpha \right)\\\left( \alpha \right) \cap \left( {ACD} \right) = Gz\end{array} \right. \Rightarrow Gz//AC\)
Trong mp(ACD), kẻ Gz // AC cắt DA tại H, khi đó H là trung điểm DA.
Do đó
\( \begin{array}{l}EF = GH = \frac{1}{2}AC\\FG = HE = \frac{1}{2}BD\end{array}\)
Mà AC = BD do hình tứ diện đều nên EF = GH = FG = HE hay EFGH là hình thoi.
Xét hai tam giác đều ABC và DBC bằng nhau (c-c-c) nên AF = DF (hai đường trung tuyến tương ứng)
Do đó tam giác ADF cân tại F.
Xét hai tam giác đều DAB và CAB bằng nhau (c-c-c) nên DE = CE (hai đường trung tuyến tương ứng)
Do đó tam giác ADF cân tại F.
Mà CE = AF nên AF = DF = DE = DE.
Suy ra hai tam giác DAF và DCE bằng nhau (c-c-c)
⇒ HF = EG (hia trung tuyến tương ứng)
Thiết diện EFGH là một hình thoi có hai đường chéo bằng nhau nên nó là một hình vuông.
Chọn đáp án: B
3.17. Giải bài 2.67 trang 87 SBT Hình học 11
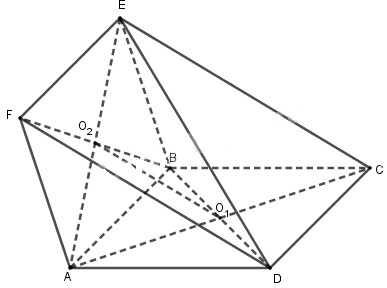
Cho hai hình bình hành ABCD và ABEF lần lượt có tâm O1, O2 và không cùng nằm trong một mặt phẳng. Khẳng định nào sau đây sai?
A. O1O2 song song với mặt phẳng (BCE).
B. O1O2 song song với mặt phẳng (BDE).
C. O1O2 song song với mặt phẳng (ADF).
D. O1O2 song song với mặt phẳng (CDE).
Phương pháp giải:
Chứng minh từng đáp án để tìm ra đáp án sai.
Hướng dẫn giải:
O1O2 là đường trung bình tam giác ACE nên O1O2 // CE ⇒ O1O2 // (BCE) nên A đúng.
Vì O1O2 ∩ (BDE) = O1 nên B sai.
O1O2 là đường trung bình tam giác BDF nên O1O2 // DF ⇒ O1O2 // (ADF) nên C đúng.
Lại có O1O2 // CE ⇒ O1O2 // (CDE) nên D đúng.
Chọn đáp án: B
3.18. Giải bài 2.68 trang 87 SBT Hình học 11
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, I lần lượt là trung điểm của các cạnh AB, SC. Mặt phẳng (α) qua M song song với mặt phẳng (BID) sẽ cắt hình chóp theo thiết diện là
A. hình tam giác B. hình lục giác
C. hình tứ giác D. hình ngũ giác
Phương pháp giải:
- Tìm giao tuyến của (α) với các mặt của hình chóp.
- Suy ra thiết diện và chọn đáp án đúng.
Hướng dẫn giải:
+) Trong (ABCD), kẻ
Gọi O, E lần lượt là giao điểm của BD, MN với AC.
+) Ta có:
\(\left\{ \begin{array}{l}\left( \alpha \right)//\left( {BID} \right)\\\left( {SAC} \right) \cap \left( {BID} \right) = IO\\\left( \alpha \right) \cap \left( {SAC} \right) = Ex\end{array} \right. \Rightarrow Ex//IO\)
Trong mp(SAC), kẻ tia Ex // IO cắt SC tại Q.
+) Ta có:
\(\left\{ \begin{array}{l}\left( \alpha \right)//\left( {BID} \right)\\\left( {SBC} \right) \cap \left( {BID} \right) = IB\\\left( \alpha \right) \cap \left( {SBC} \right) = Qy\end{array} \right. \Rightarrow Qy//IB\)
Trong mp(SBC), kẻ Qy // IB cắt SB tại K.
+) Ta có:
\(\left\{ \begin{array}{l}\left( \alpha \right)//\left( {BID} \right)\\\left( {SDC} \right) \cap \left( {BID} \right) = ID\\\left( \alpha \right) \cap \left( {SDC} \right) = Qz\end{array} \right. \Rightarrow Qz//ID\)
Trong mp(SDC), kẻ Qz // ID cắt SD tại P.
Khi đó
\( \begin{array}{l}\left( \alpha \right) \cap \left( {ABCD} \right) = MN\\\left( \alpha \right) \cap \left( {SAD} \right) = NP\\\left( \alpha \right) \cap \left( {SDC} \right) = PQ\\\left( \alpha \right) \cap \left( {SBC} \right) = QK\\\left( \alpha \right) \cap \left( {SAA} \right) = KM\end{array}\)
Do đó thiết diện là ngũ giác MNPQK.
Chọn đáp án: B
3.19. Giải bài 2.69 trang 87 SBT Hình học 11
Trong mặt phẳng (α), cho tứ giác ABCD có O là giao điểm của AC và BD. S nằm ngoài (ABCD). Giao tuyến của (SAC) và (SBD) là
A. BD B. AC C. SO D. SC
Phương pháp giải:
Tìm hai điểm chung của (SAC) và (SBD).
Hướng dẫn giải:
Ta có S ∈ (SAC) ∩ (SBD) (1)
Mà O ∈ AC ⊂ (SAC) và O ∈ BD ⊂(SBD)
⇒ O ∈ (SAC) ∩ (SBD) (2)
Từ (1) và (2) suy ra (SAC) ∩ (SBD) = SO.
Chọn đáp án: C
3.20. Giải bài 2.70 trang 87 SBT Hình học 11
Cho hình chóp S.ABCD với I = AB ∩ CD. Giao tuyến của (SAB) và (SCD) là
A. SB B. SI C. SC D. BC
Phương pháp giải:
Tìm hai điểm chung của (SAB) và (SCD).
Hướng dẫn giải:
Ta có S ∈ (SAB) ∩ (SCD) (1)
Mà I∈ AB ⊂(SAB) và I∈ CD ⊂(SCD)
⇒ I ∈ (SAB) ∩ (SCD) (2)
Từ (1) và (2) suy ra (SAB) ∩ (SCD) = SI.
Chọn đáp án: B
Tham khảo thêm
- doc Giải bài tập SBT Toán 11 Bài 1: Đại cương về đường thẳng và mặt phẳng
- doc Giải bài tập SBT Toán 11 Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song
- doc Giải bài tập SBT Toán 11 Bài 3: Đường thẳng và mặt phẳng song song
- doc Giải bài tập SBT Toán 11 Bài 4: Hai mặt phẳng song song
- doc Giải bài tập SBT Toán 11 Bài 5: Phép chiếu song song. Hình biểu diễn của một hình không gian