Giải bài tập SBT Toán 11 Bài 5: Khoảng cách

Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Chứng minh rằng khoảng cách từ các điểm A’, B, D; C, B’, D tới đường chéo AC’ bằng nhau. Tính khoảng cách đó.

Phương pháp giải:

Chứng minh AC’ là trục của đường tròn ngoại tiếp tam giác A’BD.

→ Khoảng cách từ các điểm A’, B, D; C, B’, D tới đường chéo AC’.

Hướng dẫn giải:

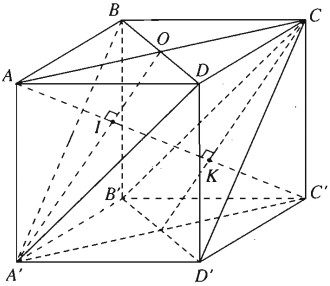
Điểm A cách đều ba đỉnh của tam giác đều A’BD vì ta có AB = AD = AA' = a

Điểm C’ cũng cách đều ba đỉnh của tam giác đều đó vì ta có C'B = C'D = C'A' = \(a\sqrt2\)

Vậy AC’ là trục của đường tròn ngoại tiếp tam giác A’BD

Tức là đường thẳng AC’ vuông góc với mặt phẳng (A’BD) tại trọng tâm I của tam giác A’BD.

Ta cần tìm khoảng cách A’I.

Ta có A'I = BI = DI = \({2 \over 3}\) A'O với O là tâm của hình vuông ABCD

Ta lại có:

\(AO' = B{\rm{D}}{{\sqrt 3 } \over 2} = a\sqrt 2.{{\sqrt 3 } \over 2} = {{a\sqrt 6 } \over 2}\)

Vậy \(A'I = {2 \over 3}A'O = {2 \over 3}.{{a\sqrt 6 } \over 2} = {{a\sqrt 6 } \over 3}\)

Tương tự điểm C’ cách đều ba đỉnh của tam giác đều CB’D’, tính được khoảng cách từ C, B’, D’ tới đường chéo AC’.

Hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a. Các cạnh bên \(SA = SB = SC = S{\rm{D}} = a\sqrt 2\). Gọi I và K lần lượt là trung điểm của AD và BC.

a) Chứng minh mặt phẳng (SIK) vuông góc với mặt phẳng (SBC). 

b) Tính khoảng cách giữa hai đường thẳng AD và SB.

Phương pháp giải:

a) Gọi O là tâm hình vuông ABCD. Chứng minh (SBC) chứa hai đường thẳng cắt nhau vuông góc với (SIK).

b) - Tìm mặt phẳng (P)chứa SB và song song với AD.

- d(AD, SB) = d(AD, (P)

Hướng dẫn giải:

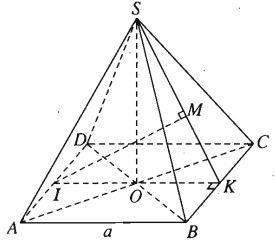
a) Gọi O là tâm hình vuông ABCD, dễ thấy I, O, K thẳng hàng. Vì K là trung điểm của BC nên \(SK \bot BC\).

Ta có

\( \left. \matrix{ BC \bot SK \hfill \cr BC \bot OK \hfill \cr} \right\} \Rightarrow BC \bot \left( {SIK} \right)\)

Do đó \(\left( {SBC} \right) \bot \left( {SIK} \right)\)

b) Hai đường thẳng AD và SB chéo nhau.

Ta có mặt phẳng (SBC) chứa SB và song song với AD.

Do đó khoảng cách giữa AD và SB bằng khoảng cách giữa AD và mặt phẳng (SBC).

Theo câu a) ta có \(\left( {SIK} \right) \bot \left( {SBC} \right)\) theo giao tuyến SK.

⇒ Khoảng cách cần tìm là IM, trong đó M là chân đường vuông góc hạ từ I tới SK.

Dựa vào hệ thức IM.SK = SO.IK ⇒ \(IM = {{SO.IK} \over {SK}}.\)

Ta lại có: \(S{K^2} = S{B^2} - B{K^2} = 2{{\rm{a}}^2} - {{{a^2}} \over 4} = {{7{a^2}} \over 4} \Rightarrow SK = {{a\sqrt 7 } \over 2}\)

 \(S{O^2} = S{A^2} - O{A^2} = 2{{\rm{a}}^2} - {\left( {{{a\sqrt 2 } \over 2}} \right)^2} = {{3{{\rm{a}}^2}} \over 2} \\ \Rightarrow SO = {{a\sqrt 3 } \over {\sqrt 2 }} = {{a\sqrt 6 } \over 2}\)

Do đó: \(IM = {{SO.IK} \over {SK}} = {{a\sqrt 6 } \over 2}.a:{{a\sqrt 7 } \over 2} = {{a\sqrt {42} } \over 7}\)

Vậy khoảng cách giữa hai đường thẳng AD và SB là bằng \({{a\sqrt {42} } \over 7}.\)

Cho hình lập phương ABCD.A’B’C’D’.

a) Chứng minh đường thẳng BC’ vuông góc với mặt phẳng (A’B’CD)

b) Xác định và tính độ dài đoạn vuông góc chung của AB’ và BC’

Phương pháp giải:

a) Chứng minh BC' vuông góc với hai đường thẳng cắt nhau thuộc (A'B'CD).

b) - Tìm (P) chứa đường thẳng AB’ và song song với BC’.

- Tìm d là hình chiếu của BC’ trên mặt phẳng (AB’D’).

- Gọi K là giao điểm của d với AB', dựng KL // BC'

→ KL là đoạn vuông góc chung cần tìm.

Hướng dẫn giải:

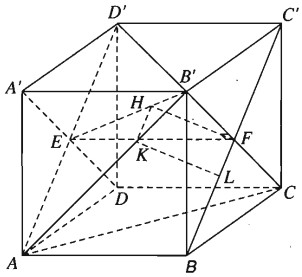
a) Ta có B’C ⊥ BC’ vì đây là hai đường chéo của hình vuông BB’C’C

Ngoài ra ta còn có: \(A'B' \bot \left( {BB'C'C} \right) \Rightarrow A'B' \bot BC'\)

Từ đó ta suy ra \(BC' \bot \left( {A'B'C{\rm{D}}} \right)\).

b) Mặt phẳng (AB’D’) chứa đường thẳng AB’ và song song với BC’.

Gọi E, F lần lượt là tâm các hình vuông ADD’A’, BCC’B’.

Kẻ FH ⊥ EB’với H ∈ EB’, khi đó FH nằm trên mặt phẳng (A’B’CD) nên theo câu a) thì \(FH \bot \left( {AB'{\rm{D'}}} \right).\)

Do đó hình chiếu BC’ trên mặt phẳng (AB’D) là đường thẳng đi qua H và song song với BC’.

Giả sử đường thẳng đó cắt AB’ tại K thì từ K vẽ đường thẳng song song với FH cắt BC’ tại L.

Khi đó KL là đoạn vuông góc chung cần dựng.

Tam giác B’EF vuông tại F nên từ công thức \({1 \over {F{H^2}}} = {1 \over {F{{\rm{E}}^2}}} + {1 \over {FB{'^2}}}\) ta tính được \(KL = FH = {{a\sqrt 3 } \over 3}\)

Cho hình chóp S.ABCD có đáy là nửa lục giác đều ABCD nội tiếp trong đường tròn đường kính AD = 2a và có cạnh SA vuông góc với mặt phẳng đáy (ABCD) với \(SA = a\sqrt 6.\)

a) Tính khoảng cách từ A và B đến mặt phẳng (SCD).

b) Tính khoảng cách từ đường thẳng AD đến mặt phẳng (SBC)

Phương pháp giải:

a) - Dựng AH vuông góc với SC → d(A, SCD) = AH.

- Gọi I là trung điểm của AD, chứng minh d(A, SCD) = 2d(B, SCD)

b) - Dựng AD vuông góc với BC tại E.

- Dựng AD vuông góc với SE tại F.

- Chứng minh d(AD, (SBC)) = AF.

Hướng dẫn giải:

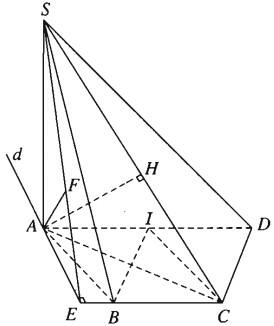
a) Vì ABCD là nửa lục giác đều nội tiếp trong đường tròn đường kính AD = 2a nên ta có:

AD // BC và AB = BC = CD = a, đồng thời \(AC \bot C{\rm{D}},AB \bot B{\rm{D}},AC = B{\rm{D}} = a\sqrt 3.\)

Như vậy:

\( \left. \matrix{ C{\rm{D}} \bot AC \hfill \cr C{\rm{D}} \bot SA \hfill \cr} \right\} \Rightarrow C{\rm{D}} \bot \left( {SAC} \right)\)

Trong mặt phẳng (SAC) dựng AH ⊥ SC tại H ta có AH ⊥ CD và AH ⊥ SC nên AH ⊥ (SCD)

Vậy AH = d(A,(SCD))

Xét tam giác SAC vuông tại A có AH là đường cao, ta có:

\( \eqalign{ & {1 \over {A{H^2}}} = {1 \over {S{A^2}}} + {1 \over {A{C^2}}} \cr & = {1 \over {{{\left( {a\sqrt 6 } \right)}^2}}} + {1 \over {{{\left( {a\sqrt 3 } \right)}^2}}} = {1 \over {2{{\rm{a}}^2}}} \cr}\)

Vậy \(A{H^2} = 2{{\rm{a}}^2} \Rightarrow AH = a\sqrt 2\)

Gọi I là trung điểm của AD ta có BI // CD nên BI song song với mặt phẳng (SCD).

Từ đó suy ra \(d\left( {B,\left( {SC{\rm{D}}} \right)} \right) = d\left( {I,\left( {SC{\rm{D}}} \right)} \right).\)

Mặt khác AI cắt (SCD) tại D nên

\( d\left( {I,\left( {SC{\rm{D}}} \right)} \right) = {1 \over 2}d\left( {A,\left( {SC{\rm{D}}} \right)} \right) = {1 \over 2}.a\sqrt 2 = {{a\sqrt 2 } \over 2}\)

Do đó: \(d\left( {B,\left( {SC{\rm{D}}} \right)} \right) = {{a\sqrt 2 } \over 2}\)

b) Vì AD // BC nên AD // SBC, do đó \(d\left( {AD,\left( {SBC} \right)} \right) = d\left( {A,\left( {SBC} \right)} \right)\)

Dựng \(AD \bot BC\) tại \(E \Rightarrow BC \bot \left( {SA{\rm{E}}} \right)\)

Dựng \(AD \bot SE\) tại F ta có:

\( \left. \matrix{ AF \bot SE \hfill \cr AF \bot BC\,\left( {vì\,BC \bot \left( {SAE} \right)} \right) \hfill \cr} \right\} \Rightarrow AF \bot \left( {SBC} \right)\)

Vậy \(AF = d\left( {A,\left( {SBC} \right)} \right) = d\left( {AD,\left( {SBC} \right)} \right)\)

Xét tam giác vuông AEB ta có: \(AE = AB\sin \widehat {ABE} = a\sin {60^0} = {{a\sqrt 3 } \over 2}\)

Xét tam giác SAE vuông tại A ta có:

\( {1 \over {A{F^2}}} = {1 \over {S{A^2}}} + {1 \over {A{E^2}}} = {1 \over {{{\left( {a\sqrt 6 } \right)}^2}}} + {1 \over {\left( {{{a\sqrt 3 } \over 2}} \right)}} = {9 \over {6{a^2}}}\)

Do đó \(A{F^2} = {{6{a^2}} \over 9} \Rightarrow AF = {{a\sqrt 6 } \over 3}\)

Vậy \(d\left( {AD,\left( {SBC} \right)} \right) = AF = {{a\sqrt 6 } \over 3}\)

Tính khoảng cách giữa hai cạnh đối trong một tứ diện đều cạnh a. 

Phương pháp giải:

Khoảng cách giữa hai cạnh đối bằng độ dài đoạn thẳng nói trung điểm hai cạnh đó.

Hướng dẫn giải:

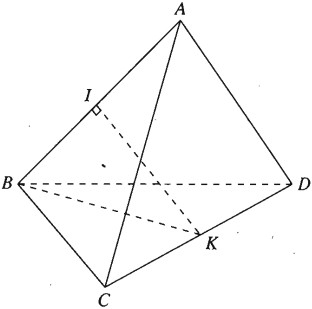
Giả thiết cho ABCD là tứ diện đều nên các cặp cạnh đối diện của tứ diện đó có vai trò như nhau.

Do đó ta chỉ cần tính khoảng cách giữa hai cạnh AB và CD là đủ. 

Gọi I và K lần lượt là trung điểm của AB và CD.

Tam giác BCD và ACD đều cạnh a nên hai đường trung tuyến \(BK = AK = \dfrac{{a\sqrt 3 }}{2}\) 

Hay tam giác ABK cân tại K.

I là trung điểm AB nên \(KI \bot AB.\)

Tương tự ta có \(IK \bot CD.\)

Do đó IK là đoạn vuông góc chung của AB và CD nên nó chính là khoảng cách giữa AB và CD.

Tam giác BKI vuông tại I. Ta có:

\( I{K^2} = B{K^2} - B{I^2} = {\left( {{{a\sqrt 3 } \over 2}} \right)^2} - {\left( {{a \over 2}} \right)^2} = {{{a^2}} \over 2}\)

Vậy \(IK = {{a\sqrt 2 } \over 2}.\)

Tính khoảng cách giữa hai cạnh AB và CD của hình tứ diện ABCD biết rằng \(AC = BC = AD = BD = a\) và AB = p, CD = q.

Phương pháp giải:

Khoảng cách giữa hai cạnh AB và CD bằng độ dài đoạn thẳng nói trung điểm hai cạnh đó.

Hướng dẫn giải:

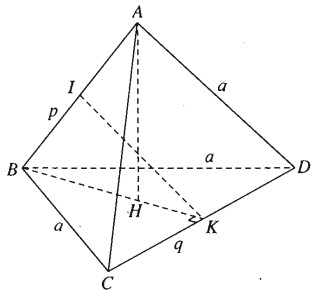
Gọi I và K lần lượt là trung điểm của AB và CD.

Ta có: \(\Delta ACD = \Delta BCD\left( {c - c - c} \right) \)nên AK = BK (hai đường trung tuyến tương ứng)

\( \Rightarrow \Delta ABK\) cân tại K có I là trung điểm AB nên \(KI \bot AB.\)

Tương tự ta có \(IK \bot CD\) nên IK là đoạn vuông góc chung của AB, CD.

Độ dài đoạn IK là khoảng cách cần tìm:

\( I{K^2} = B{K^2} - B{I^2} = B{K^2} - {{{p^2}} \over 4}\)

Mà \(B{K^2} = B{C^2} - C{K^2} = {a^2} - {{{q^2}} \over 4}\)

Vậy \(I{K^2} = {a^2} - {{{p^2} + {q^2}} \over 4}\)

Do đó \(IK = {1 \over 2}\sqrt {4{{\rm{a}}^2} - \left( {{p^2} + {q^2}} \right)}\) với điều kiện \(4{{\rm{a}}^2} - \left( {{p^2} + {q^2}} \right) > 0.\)

Hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Gọi G là trọng tâm của tam giác đáy ABC.

a) Tính khoảng cách từ S tới mặt phẳng đáy (ABC).

b) Tính khoảng cách giữa hai đường thẳng AB và SG

Phương pháp giải:

a) - d(S, (ABC) = SG

- Áp dụng định lý Pytago trong tam gác SAG để tính SG.

b) - d(AB, HG) = GH.

- Áp dụng tính chất trọng tâm để tính GH.

Hướng dẫn giải:

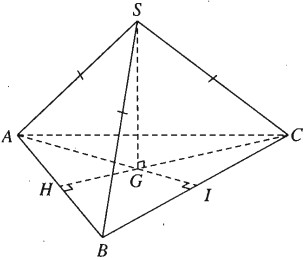
a) SG là trục đường tròn ngoại tiếp tam giác đều ABC nên SG ⊥ (ABC). Ta có 

\( \eqalign{ & S{G^2} = S{A^2} - A{G^2} \cr & = {\left( {2{\rm{a}}} \right)^2} - {\left[ {{2 \over 3}\left( {{{3{\rm{a}}\sqrt 3 } \over 2}} \right)} \right]^2} \cr & = 4{{\rm{a}}^2} - 3{{\rm{a}}^2} = {a^2} \cr} \)

Vậy khoảng cách từ S tới mặt phẳng (ABC) là độ dài của đoạn SG = a

b) Ta có CG ⊥ AB tại H.

Vì GH là đoạn vuông góc chung của AB và SG

Do đó \(HG = {1 \over 3}HC\) mà \(HC = {{3{\rm{a}}\sqrt 3 } \over 2}\) nên \(HG = {{a\sqrt 3 } \over 2}.\)

Cho hình lăng trụ tam giác ABC.A’B’C’có tất cả các cạnh bên và cạnh đáy đều bằng a. Các cạnh bên của lăng trụ tạo với mặt phẳng đáy góc 60° và hình chiếu vuông góc của đỉnh A lên mặt phẳng (A’B’C’) trùng với trung điểm của cạnh B’C’.

a) Tính khoảng cách giữa hai mặt phẳng đáy của lăng trụ

b) Chứng minh rằng mặt bên BCC’B’ là một hình vuông.

Phương pháp giải:

a) Gọi I là trung điểm của B'C'. Chứng minh khoảng cách cần tìm là đoạn AI.

b) Chứng minh BCC'B' là hình thoi có một góc vuông → hình vuông.

Hướng dẫn giải:

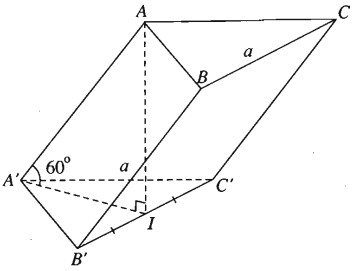
a) Gọi I là trung điểm của cạnh B’C’.

Theo giả thiết ta có AI ⊥ (A’B’C’) và \(\widehat {AA'I} = {60^0}\).

Ta có:  (ABC) // (A’B’C’).

Nên khoảng cách giữa hai mặt phẳng chính là khoảng cách AI.

Do đó \(AI = AA'.\sin {60^0} = a.{{\sqrt 3 } \over 2} = {{a\sqrt 3 } \over 2}\)

b)

\(\left. \matrix{ B'C' \bot A'I \hfill \cr B'C' \bot AI \hfill \cr} \right\} \Rightarrow B'C' \bot \left( {AIA'} \right)\) \( \Rightarrow B'C' \bot AA'\)

Mà AA' // BB' // CC' nên B’C’ ⊥ BB’

Vậy mặt bên BCC’B’ là một hình vuông vì nó là hình thoi có một góc vuông.