Giải bài tập SBT Toán 11 Bài 3: Đường thẳng và mặt phẳng song song

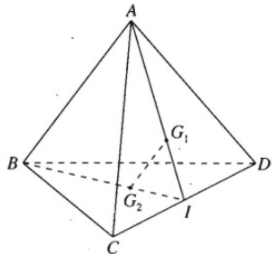
Cho tứ diện ABCD. Gọi $G_1$ và $G_2$ lần lượt là trọng tâm của tam giác ACD và BCD. Chứng minh rằng $G_1G_2$ song song với các mặt phẳng (ABC) và (ABD).

Phương pháp giải:

Sử dụng định lý Talet để chứng minh $G_1G_2$ song song với một đường thẳng nằm trong các mặt phẳng (ABC) và (ABD).

Hướng dẫn giải:

Gọi I là trung điểm CD

Ta có G₁ là trọng tâm tam giác ACD nên ta có $\dfrac{IG_1}{IA}=\dfrac{1}{3}$

Và G₂ là trọng tâm tam giác BCD nên ta có $\dfrac{IG_2}{IB}=\dfrac{1}{3}.$

Khi đó $\dfrac{IG_1}{IA}=\dfrac{IG_2}{IB}=\dfrac{1}{3}$

Theo Talet ta được G₁G₂ // AB.

Do $\left\{ \begin{array}{l}{G_1}{G_2}// AB\\AB \subset (ABC)\end{array} \right.$

$\Rightarrow G_1G_2// (ABC).$

Do $\left\{ \begin{array}{l}{G_1}{G_2}// AB\\AB \subset (ABD)\end{array} \right.$

$\Rightarrow G_1G_2// (ABD).$

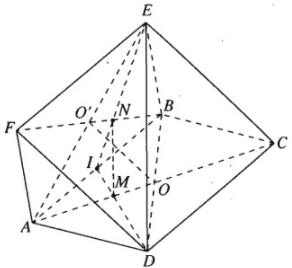
Cho hai hình bình hành ABCD và ABEF nằm trong hai mặt phẳng phân biệt. Gọi O là giao điểm của AC và BD, O’ là giao điểm của AE và BF.

a) Chứng minh rằng OO’ song song với hai mặt phẳng (ADF) và (BCE)

b) Gọi M và N lần lượt là trọng tâm của các tam giác ABD và ABE. Chứng minh rằng MN // (CEF). 

Phương pháp giải:

a) Chứng minh OO’ song song với DF và CE.

b) Chứng minh MN // DE và DE thuộc  (CEF)

Hướng dẫn giải:

a) Ta có tứ giác ABCD là hình bình hành, $O=AC\cap BD$ nên O là trung điểm của AC, BD.

Tứ giác ABEF là hình bình hành, $O’=AE\cap BF$ nên O’ là trung điểm của AE, BF

Xét tam giác BFD có O là trung điểm của BD, O’ là trung điểm của BF

Theo tính chất đường trung bình của tam giác ta có OO’// DF

Mà $DF\subset (ADF)$

$\Rightarrow OO’// (ADF)$

Xét tam giác ACE có O là trung điểm của AC, O’ là trung điểm của AE

Theo tính chất đường trung bình của tam giác ta có OO’// CE

Mà $CE\subset (BCE)$

$\Rightarrow OO’// (BCE).$

b) Gọi I là trung điểm AB.

Trong tam giác ABD có M là trọng tâm nên ta có $\dfrac{IM}{ID}=\dfrac{1}{3}.$

Trong tam giác ABE có N là trọng tâm nên ta có $\dfrac{IN}{IE}=\dfrac{1}{3}.$

Suy ra $\dfrac{IM}{ID}=\dfrac{IN}{IE}=\dfrac{1}{3}.$

Theo định lý Talet suy ra MN // DE (1)

Mà do tứ giác ABCD là hình bình hành nên AB song song và bằng với CD

Và tứ giác ABEF là hình bình hành nên AB song song và bằng với EF

Suy ra CD song song và bằng với EF ⇒ CEFD là hình bình hành

$DE\subset (CEF)\text{(2)}$

Từ (1) và (2) ⇒ MN // (CEF).

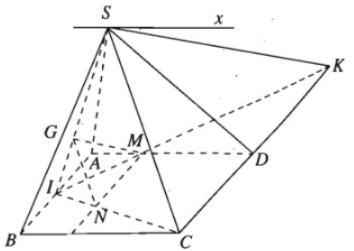
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi G là trọng tâm của tam giác SAB và I là trung điểm của AB. Lấy điểm M trong đoạn AD sao cho AD = 3AM.

a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC).

b) Đường thẳng qua M song song với AB cắt CI tại N. Chứng minh rằng $NG// \left( {SC{\rm{D}}} \right).$

c) Chứng minh rằng MG // (SCD).

Phương pháp giải:

a) Chứng minh (SAD) và (SBC) chưa hai đường thẳng song song.

→ Giao tuyến cần tìm song song với hai đường thẳng đó.

b) Chứng minh GN // SC.

c) - Gọi K là giao điểm của IM và CD.

- Chứng minh MG // SK.

Hướng dẫn giải:

a) Ta có $S=(SAD)\cap (SBC)$

$\left\{ \begin{array}{l}AD \subset (SAD)\\BC \subset (SBC)\\AD// BC\end{array} \right. \\ \Rightarrow (SAD)\cap (SBC)=Sx; Sx// AD// BC.$

b) Ta có: MN // AI // CD theo định lý Talet ta được $\dfrac{IN}{IC}=\dfrac{AM}{AD}=\dfrac{1}{3}.$

Mặt khác: G là trọng tâm tam giác SAB nên $\dfrac{IG}{IS}=\dfrac{1}{3}.$

Suy ra: $\dfrac{IN}{IC}=\dfrac{IG}{IS}=\dfrac{1}{3}.$

Theo định lý Talet ta được GN // SC mà $SC\subset (SCD).$

$\Rightarrow GN// (SCD).$

c) Gọi $K=IM\cap CD \Rightarrow K\in CD \Rightarrow K\in (SCD) \Rightarrow SK\subset (SCD)$

Ta có MN // CD

Theo Talet ta có $\dfrac{MN}{CK}=\dfrac{IN}{IC}=\dfrac{1}{3}$

$\Rightarrow \dfrac{IM}{IK}=\dfrac{1}{3}$

Mà G là trong tâm tam giác SAB nên $\dfrac{IG}{IS}=\dfrac{1}{3}$

Suy ra $\dfrac{IM}{IK}=\dfrac{IG}{IS}=\dfrac{1}{3}$

⇒ GM // SK mà $SK\subset (SCD).$

Nên GM // (SCD).

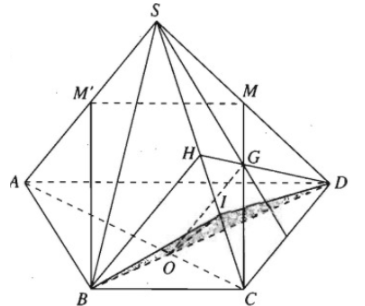
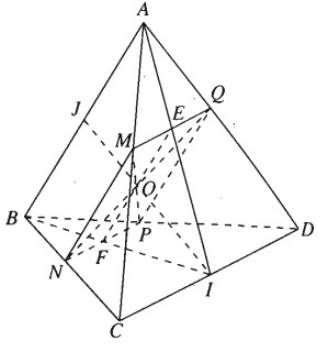
Cho hình chóp S.ABCD có đáy là hình thang ABCD, đáy lớn là AD và AD = 2BC. Gọi O là giao điểm của AC và BD, G là trọng tâm của tam giác SCD.

a) Chứng minh rằng OG // (SBC).

b) Cho M là trung điểm của SD. Chứng minh rằng CM // (SAB).

c) Giả sử điểm I nằm trong đoạn SC sao cho $S{\rm{C = }}\dfrac{3 }{2}SI$. Chứng minh rằng SA // (BID).

Phương pháp giải:

a) Gọi H là trung điểm SC, chứng minh OG // BH → OG // (SBC).

b) Gọi M' là trung điểm SA, chứng minh CM // M'B → CM // (SAB).

c) Chứng minh IO // SA → SA // (BID).

Hướng dẫn giải:

a) Tứ giác ABCD là hình thang có AD song song và gấp đôi BC.

Theo định lý Talet $\dfrac{OD}{OB}=\dfrac{OA}{OC}=\dfrac{AD}{BC}=2$

$\Rightarrow \dfrac{OD}{BD}=\dfrac{OD}{OB+OD} =\dfrac{2}{1+2}=\dfrac{2}{3}\text{(1)}.$

Gọi H là trung điểm của SC, tam giác SCD có G là trọng tâm nên $\dfrac{DG}{DH}=\dfrac{2}{3}\text{(2)}.$

Từ (1) và (2) suy ra $\dfrac{DO}{DB}=\dfrac{DG}{DH}=\dfrac{2}{3}$

Theo định lý Talet OG // BH (*)

Mà $H\in SC\Rightarrow H\in (SBC)$

$\Rightarrow BH\subset (SBC)\text{(**)}$

Từ (*) và (**) suy ra  OG // (SBC).

b) Gọi M’ là trung điểm của SA và ta có M là trung điểm SD nên trong tam giác SAD khi đó MM’ là đường trung bình.

⇒ MM' song song và bằng nửa AD.

Mà hình thang ABCD có BC song song và bằng nửa AD.

Suy ra MM’ song song và bằng BC 

⇒ Tứ giác MM’BC là hình bình hành.

⇒ MC // M’B

Ta lại có $M’B\subset (SAB)$

$\Rightarrow MC// (SAB).$

c) Ta có: $SC=\dfrac{3}{2}SI \Rightarrow \dfrac{CI}{CS}=\dfrac{1}{3}.$

Mà $\dfrac{OC}{OA}=\dfrac{BC}{AD}=\dfrac{1}{2}$ nên $\dfrac{CO}{CA}=\dfrac{1}{3}.$

Suy ra $\dfrac{CI}{CS}=\dfrac{CO}{CA}=\dfrac{1}{3}$

Theo định lý Talet ta được IO // SA mà $IO\subset (BID)$

$\Rightarrow SA// (BID).$

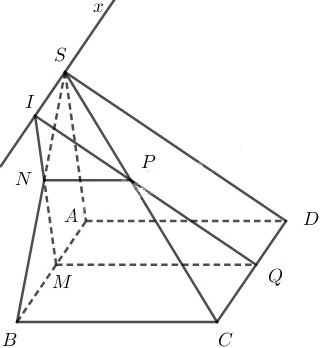
Cho tứ diện ABCD. Qua điểm M nằm trên AC ta dựng một mặt phẳng \left( \alpha \right) song song với AB và CD. Mặt phẳng này lần lượt cắt các cạnh BC, BD và AD tại N, P và Q.

a) Tứ giác MNPQ là hình gì?

b) Gọi O là giao điểm hai đường chéo của tứ giác MNPQ. Tìm tập hợp các điểm O khi M di động trên đoạn AC. 

Phương pháp giải:

a) Chứng minh tứ giác có hai cặp cạnh đối song song.

b) Sử dụng định lý Talet.

Hướng dẫn giải:

a) Ta có:

$\left\{\begin{array}{l}(\alpha )// AB\\AB \subset (ABC)\ \alpha ) \cap (ABC) = MN\end{array} \right. \Rightarrow MN// AB$

$\left\{ \begin{array}{l}(\alpha )// CD\\CD \subset (BCD)\ \alpha ) \cap (BCD) = NP\end{array} \right. \Rightarrow CD// NP$

$\left\{ \begin{array}{l}(\alpha )// AB\\AB \subset (ABD)\ \alpha )\cap (ABD) = PQ\end{array} \right. \Rightarrow PQ// AB$

$\left\{ \begin{array}{l}(\alpha )// CD\\CD \subset (ACD)\ \alpha )\cap (ACD) = MQ\end{array} \right. \Rightarrow MQ// CD$

Do đó MN // PQ và NP // MQ.

Vậy tứ giác MNPQ là hình bình hành.

b) Ta có $MP\cap NQ=O$. Gọi I là trung điểm của CD.

Trong tam giác ACD có MQ // CD $\Rightarrow AI\cap MQ=E$, E là trung điểm của MQ.

Trong tam giác BCD có NP // CD $\Rightarrow BI\cap NP=F$, F là trung điểm của MQ.

Khi đó EF là đường trung bình của hình bình hành MNPQ 

⇒ EF // MN và O là trung điểm của EF.

Trong tam giác ABI có EF // AB, O là trung điểm của EF

Khi đó $IO\cap AB=J$, J là trung điểm của AB.

⇒ I, O, J thẳng hàng, O thuộc IJ cố định.

Vì M di động trên AC nên O chạy trong đoạn IJ.

Vậy tập hợp các điểm O là đoạn IJ.

Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. M là một điểm di động trên đoạn AB. Một mặt phẳng \left( \alpha \right) đi qua M và song song với SA và BC; $\left( \alpha \right)$ cắt SB, SC và CD lần lượt tại N, P và Q.

a) Tứ giác MNPQ là hình gì?

b) Gọi I là giao điểm của MN và PQ. Chứng minh rằng I nằm trên một đường thẳng cố định

Phương pháp giải:

a) Chứng minh tứ giác có hai cạnh đối song song.

b) Chứng minh I thuộc giao tuyến của (SAB) và (SCD)

Hướng dẫn giải:

a) Ta có:

$\left\{ \begin{array}{l}(\alpha )// SA\\SA \subset (SAB)\ \alpha ) \cap (SAB) = MN\end{array} \right. \Rightarrow MN// SA$

$\left\{ \begin{array}{l}(\alpha )// BC\\BC \subset (SBC)\ \alpha ) \cap (SBC) = NP\end{array} \right. \Rightarrow NP// BC \text{(1)}$

$\left\{ \begin{array}{l}(\alpha )// BC\\BC \subset (ABCD)\ \alpha ) \cap (ABCD) = MQ\end{array} \right. \Rightarrow BC// MQ \text{(2)}$

Từ (1) và (2)  NP // QM // BC

⇒ MNPQ là hình thang có hai đáy là NP, QM.

b) Ta có:

$\left\{ \begin{array}{l}S \in (SAB) \cap (SCD)\\AB \subset (SAB),CD \subset (SCD)\\AB// CD\end{array} \right. \\ \Rightarrow (SAB) \cap (SCD) = Sx; Sx// AB// CD$

Ta có: $I=MN\cap PQ$

$\Rightarrow I\in MN, MN\subset (SAB) \Rightarrow I\in (SAB).$

Và $PQ\subset (SCD)\Rightarrow I\in (SCD).$

$\Rightarrow I\in (SAB)\cap (SCD) \Rightarrow I\in Sx.$

Do (SAB) và (SCD) cố định ⇒ AB, CD cố định

 Sx // AB // CD ⇒ Sx cố định

$I\in Sx\Rightarrow I$ cố định.