Giải bài tập SBT Toán 11 Bài 5: Phép quay
eLib giới thiệu đến các em tài liệu hướng dẫn giải bài tập SBT Hình học 11 Bài 5: Phép quay. Với nội dung chi tiết, rõ ràng giúp các em ôn tập lại các kiến thức đã học và vận dụng vào giải các bài tập tương tự. Mời các em cùng theo dõi.
Mục lục nội dung

1. Giải bài 1.15 trang 24 SBT Hình học 11
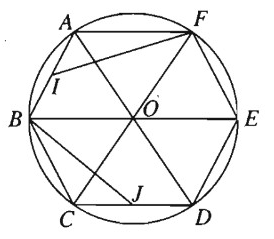
Cho lục giác đều ABCDEF, O là tâm đối xứng của nó, I là trung điểm của AB.
a) Tìm ảnh của tam giác AIF qua phép quay tâm O góc \( {120}^o\);
b) Tìm ảnh của tam giác AOF qua phép quay tâm E góc \({60}^o.\)
Phương pháp giải:
Cho O và góc lượng giác \(\alpha\). Phép quay tâm O góc \(\alpha\) biến:
- O thành chính nó,
- M khác O thành điểm M’ sao cho OM’ = OM và góc lượng giác (OM;OM’) bằng \(\alpha\).
Hướng dẫn giải:
a) Phép quay tâm O góc \({120}^o\) biến F, A, B lần lượt thành B, C, D; biến trung điểm I của AB thành trung điểm J của CD.
Nên nó biến tam giác AIF thành tam giác CJB.
b) Phép quay tâm E góc \({60}^o\) biến A, O, F lần lượt thành C, D, O.
2. Giải bài 1.16 trang 24 SBT Hình học 11
Trong mặt phẳng Oxy cho các điểm A(3;3), B(0;5), C(1;1) và đường thẳng d có phương trình \(5x-3y+15=0\). Hãy xác định tọa độ các đỉnh của tam giác A’B’C’ và phương trình của đường thẳng d’ theo thứ tự là ảnh của tam giác ABC và đường thẳng d qua phép quay tâm O, góc quay \({90}^o\).
Phương pháp giải:
Cho O và góc lượng giác \(\alpha\). Phép quay tâm O góc \(\alpha\) biến:
- O thành chính nó,
- M khác O thành điểm M’ sao cho OM’ = OM và góc lượng giác (OM;OM’) bằng \(\alpha\).
Hướng dẫn giải:
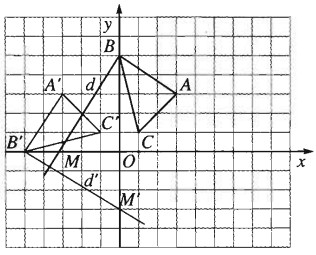
Gọi \(Q_{(O,{90}^o)}\) là phép quay tâm O, góc quay \({90}^o\).
Điểm A’ = (-3;3), B’ = (-5;0), C’ = (-1;1).
Đường thẳng d đi qua B và M(-3;0).
Ta có \(M’=Q_{(O,{90}^o)}(M)=(0;-3)\) nên d’ là đường thẳng B’M’ có phương trình \(3x+5y+15=0\).
3. Giải bài 1.17 trang 25 SBT Hình học 11
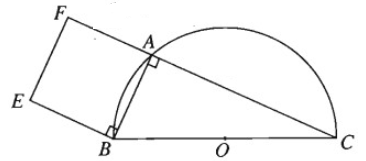
Cho nửa đường tròn tâm O đường kính BC. Điểm A chạy trên nửa đường tròn đó. Dựng về phía ngoài của tam giác ABC hình vuông ABEF. Chứng minh rằng E chạy trên một nửa đường tròn cố định.
Phương pháp giải:
Cho O và góc lượng giác \(\alpha\). Phép quay tâm O góc \(\alpha\)biến:
- O thành chính nó,
- M khác O thành điểm M’ sao cho OM’ = OM và góc lượng giác (OM;OM’) bằng \(\alpha\).
- Phép quay bảo toàn khoảng cách hai điểm.
Hướng dẫn giải:
Xem E là ảnh của A qua phép quay tâm B, góc \({90}^o\).
Khi A chạy trên nửa đường tròn (O), E sẽ chạy trên nửa đường tròn (O’) là ảnh của nửa đường tròn (O) qua phép quay tâm B, góc \({90}^o\).
4. Giải bài 1.18 trang 25 SBT Hình học 11
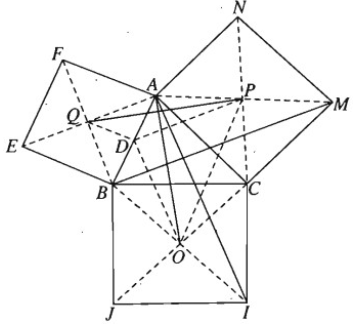
Cho tam giác ABC. Dựng về phía ngoài của tam giác các hình vuông BCIJ, ACMN, ABEF và gọi O, P, Q lần lượt là tâm đối xứng của chúng
a) Gọi D là trung điểm của AB. Chứng minh rằng DOP là tam giác vuông cân đỉnh D;
b) Chứng minh AO vuông góc với PQ và AO = PQ.
Phương pháp giải:
Cho O và góc lượng giác \(\alpha\). Phép quay tâm O góc \(\alpha\)biến:
- O thành chính nó,
- M khác O thành điểm M’ sao cho OM’ = OM và góc lượng giác (OM;OM’) bằng \(\alpha\).
- Biến một đoạn thẳng thành đoạn thẳng bằng đoạn thẳng đã cho.
Hướng dẫn giải:
a) Phép quay tâm C góc \({90}^o\) biến MB thành AI.
Do đó MB bằng và vuông góc với AI.
DP song song và bằng nửa BM.
DO song song và bằng nửa AI.
Từ đó suy ra DP bằng và vuông góc với DO.
Vậy tam giác DPO vuông tại D.
b) Từ câu a) suy ra phép quay tâm D, góc \({90}^o\) biến O thành P, biến A thành Q.
Do đó OA bằng và vuông góc với PQ.
Tham khảo thêm
- doc Giải bài tập SBT Toán 11 Bài 1+Bài 2: Phép biến hình. Phép tịnh tiến
- doc Giải bài tập SBT Toán 11 Bài 3: Phép đối xứng trục
- doc Giải bài tập SBT Toán 11 Bài 4: Phép đối xứng tâm
- doc Giải bài tập SBT Toán 11 Bài 6: Khái niệm về phép dời hình và hai hình bằng nhau
- doc Giải bài tập SBT Toán 11 Bài 7: Phép vị tự
- doc Giải bài tập SBT Toán 11 Bài 8: Phép đồng dạng
- doc Giải bài tập SBT Hình học 11 Ôn tập chương 1: Phép dời hình và phép đồng dạng