Giải bài tập SGK Toán 11 Nâng cao Bài 2: Đạo hàm của các hàm số lượng giác

Tìm các giới hạn sau:

a) $\mathop {\lim }\limits_{x \to 0} {{\tan 2x} \over {\sin 5x}}$

b) $\mathop {\lim }\limits_{x \to 0} {{1 - {{\cos }^2}x} \over {x\sin 2x}}$

c) $\mathop {\lim }\limits_{x \to 0} {{1 + \sin x - \cos x} \over {1 - \sin x - \cos x}}$

Phương pháp giải:

a) b) Sử dụng công thức giới hạn $\mathop {\lim }\limits_{x \to 0} \dfrac{{\sin x}}{x} = 1$.

c) Phân tích tử và mẫu thành nhân tử và rút gọn khử dạng vô định.

Hướng dẫn giải:

a) $\mathop {\lim }\limits_{x \to 0} {{\tan 2x} \over {\sin 5x}}$

$= \mathop {\lim }\limits_{x \to 0} {{\sin 2x} \over {\cos 2x.\sin 5x}}$

$= \mathop {\lim }\limits_{x \to 0} \left[ {\frac{{\sin 2x}}{{2x}}.\frac{{2x}}{{\cos 2x\sin 5x}}} \right]\\= \mathop {\lim }\limits_{x \to 0} \left[ {\frac{1}{{\cos 2x}}.\frac{{\sin 2x}}{{2x}}.\frac{{\frac{{2x}}{{5x}}}}{{\frac{{\sin 5x}}{{5x}}}}} \right] \\= \mathop {\lim }\limits_{x \to 0} \left[ {\frac{2}{{5\cos 2x}}.\frac{{\sin 2x}}{{2x}}.\frac{1}{{\frac{{\sin 5x}}{{5x}}}}} \right] \\ = \frac{2}{{5\cos 0}}.1.1 = \frac{2}{5}$

b) $\mathop {\lim }\limits_{x \to 0} {{1 - {{\cos }^2}x} \over {x\sin 2x}}$

$= \mathop {\lim }\limits_{x \to 0} {{{{\sin }^2}x} \over {2x\sin x\cos x}}$ $= \mathop {\lim }\limits_{x \to 0} {{\sin x} \over {2x\cos x}}$

$= \mathop {\lim }\limits_{x \to 0} \left[ {\frac{1}{{2\cos x}}.\frac{{\sin x}}{x}} \right] \\= \frac{1}{{2\cos 0}}.1 = \frac{1}{2}$

$\eqalign{c) & \mathop {\lim }\limits_{x \to 0} {{1 + \sin x - \cos x} \over {1 - \sin x - \cos x}} \cr & = \mathop {\lim }\limits_{x \to 0} \frac{{\left( {1 - \cos x} \right) + \sin x}}{{\left( {1 - \cos x} \right) - \sin x}}\cr &= \mathop {\lim }\limits_{x \to 0} {{2\sin^2 {x \over 2} + 2\sin {x \over 2}\cos {x \over 2}} \over {2{{\sin }^2}{x \over 2} - 2\sin {x \over 2}\cos {x \over 2}}} \cr & = \mathop {\lim }\limits_{x \to 0} \frac{{2\sin \frac{x}{2}\left( {\sin \frac{x}{2} + \cos \frac{x}{2}} \right)}}{{2\sin \frac{x}{2}\left( {\sin \frac{x}{2} - \cos \frac{x}{2}} \right)}}\cr &= \mathop {\lim }\limits_{x \to 0} {{\sin {x \over 2} + \cos {x \over 2}} \over {\sin {x \over 2} - \cos {x \over 2}}} \cr & = \frac{{\sin 0 + \cos 0}}{{\sin 0 - \cos 0}} = \frac{1}{{ - 1}} = - 1 \cr}$

Tìm đạo hàm của các hàm số sau:

a) $y = 5\sin x - 3\cos x$

b) $y = \sin \left( {{x^2} - 3x + 2} \right)$

c) $y = \cos \sqrt {2x + 1}$

d) $y = 2\sin 3x\cos 5x$

e) $y = {{\sin x + \cos x} \over {\sin x - \cos x}}$

f) $y = \sqrt {\cos 2x}$

Phương pháp giải:

a) Sử dụng các công thức $(\sin x)'=\cos x$ và $(\cos x)'=-\sin x$.

b) Sử dụng công thức $(\sin u)'=u'\cos u$.

c) Sử dụng công thức $(\cos u)'=-u'\sin u$.

d) Biến đổi tích thành tổng và tính đạo hàm.

e) Sử dụng công thức đạo hàm của một thương $\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{{{v^2}}}$.

f) Sử dụng công thức $\left( {\sqrt u } \right)' = \frac{{u'}}{{2\sqrt u }}$.

Hướng dẫn giải:

a) $y' = 5\cos x + 3\sin x$

b) $y'=\left[ {\sin \left( {{x^2} - 3x + 2} \right)} \right]'$

$= \left( {{x^2} - 3x + 2} \right)'\cos \left( {{x^2} - 3x + 2} \right)\\= \left( {2x - 3} \right)\cos \left( {{x^2} - 3x + 2} \right)$

c) $y' = - \left( {\sqrt {2x + 1} } \right)'\sin \sqrt {2x + 1}$

$= - \frac{{\left( {2x + 1} \right)'}}{{2\sqrt {2x + 1} }}\sin \sqrt {2x + 1} \\= -{2 \over {2\sqrt {2x + 1} }}\left( { \sin \sqrt {2x + 1} } \right)\\= {{ - \sin \sqrt {2x + 1} } \over {\sqrt {2x + 1} }}$

d) $y = 2.\frac{1}{2}\left[ {\sin \left( {3x + 5x} \right) + \sin \left( {3x - 5x} \right)} \right]$

$= \sin 8x + \sin \left( { - 2x} \right)\\= \sin 8x - \sin x\\\Rightarrow y' = \left( {8x} \right)'\cos 8x - \left( {2x} \right)'\cos 2x\\= 8\cos 8x - 2\cos 2x$

e) $y' = {{\left( {\cos x - \sin x} \right)\left( {\sin x - \cos x} \right) - {{\left( {\cos x + \sin x} \right)}^2}} \over {{{\left( {\sin x - \cos x} \right)}^2}}}$

$= {{ - 2} \over {{{\left( {\sin x - \cos x} \right)}^2}}}$

f) $y' = \frac{{\left( {\cos 2x} \right)'}}{{2\sqrt {\cos 2x} }}$

$= \frac{{\left( {2x} \right)'.\left( { - \sin 2x} \right)}}{{2\sqrt {\cos 2x} }}\\= {{ - 2\sin 2x} \over {2\sqrt {\cos 2x} }} \\ = {-{\sin 2x} \over {\sqrt {\cos 2x} }}$

Chứng minh rằng hàm số $y = {\sin ^6}x + {\cos ^6}x + 3{\sin ^2}x{\cos ^2}x$ có đạo hàm bằng 0.

Phương pháp giải:

Chứng minh hàm số y là một hàm hằng.

Hướng dẫn giải:

Ta có:

$\eqalign{ & y = \left( {{{\sin }^2}x + {{\cos }^2}x} \right)\left( {{{\sin }^4}x - {{\sin }^2}x{{\cos }^2}x + {{\cos }^4}x} \right) + 3{\sin ^2}x{\cos ^2}x \cr & = {\sin ^4}x + 2{\sin ^2}x{\cos ^2}x + {\cos ^4}x \cr & = {\left( {{{\sin }^2}x + {{\cos }^2}x} \right)^2} = 1 \cr & \Rightarrow y' = 0 \cr}$

Tìm đạo hàm của các hàm số sau:

a) $y = \tan {{x + 1} \over 2}$

b) $y = \cot \sqrt {{x^2} + 1}$

c) $y = {\tan ^3}x + \cot 2x$

d) $y = \tan 3x - \cot 3x$

e) $y = \sqrt {1 + 2\tan x}$

f) $y = x\cot x$

Phương pháp giải:

a) Sử dụng các công thức tính đạo hàm:

$\left( {\tan u} \right)' = \dfrac{u'}{{{{\cos }^2}u}}$

$\left( {\dfrac{u}{v}} \right)' = \dfrac{{u'v - uv'}}{{{v^2}}}$

$\left( {{x^n}} \right)' = n{x^{n - 1}}$

b) Sử dụng các công thức tính đạo hàm:

$\cos u = -u'\sin u$

$\left( {\sqrt u } \right)' = \dfrac{u'}{{2\sqrt u }}$

$\left( {{x^n}} \right)' = n{x^{n - 1}}$

c) Sử dụng các công thức đạo hàm:

- Công thức đạo hàm hợp

- Các công thức đạo hàm của các hàm số sơ cấp:

$\left( {\tan x} \right)' = \dfrac{1}{{{{\cos }^2}x}}$

$\left( {\cot u} \right)' = - \dfrac{u'}{{{{\sin }^2}u}}$

d) Sử dụng các công thức tính đạo hàm:

$\left( {\tan u} \right)' = \dfrac{u'}{{{{\cos }^2}u}}$

$\left( {\cot u} \right)' = - \dfrac{u'}{{{{\sin }^2}u}}$

e) Sử dụng các công thức tính đạo hàm:

$\left( {\sqrt u } \right)' = \dfrac{u'}{{2\sqrt u }}$

$\left( {\tan x} \right)' = \dfrac{1}{{{{\cos }^2}x}}$

f) Sử dụng các công thức tính đạo hàm:

$u.v=u'v+uv'$

$\left( {\cot x} \right)' = - \dfrac{1}{{{{\sin }^2}x}}$

Hướng dẫn giải:

a) $y' = \left( {\dfrac{{x + 1}}{2}} \right)'.\dfrac{1}{{{{\cos }^2}\dfrac{{x + 1}}{2}}}$

$= {1 \over {2{{\cos }^2}{{x + 1} \over 2}}}$

b) $y' = \left( {\sqrt {{x^2} + 1} } \right)'.\dfrac{{ - 1}}{{{{\sin }^2}\sqrt {{x^2} + 1} }}$

$= \left( {{x^2} + 1} \right)'.\dfrac{1}{{2\sqrt {{x^2} + 1} }}.\dfrac{{ - 1}}{{{{\sin }^2}\sqrt {{x^2} + 1} }}\\= \dfrac{{ - 2x}}{{2\sqrt {{x^2} + 1} }}.\dfrac{1}{{{{\sin }^2}\sqrt {{x^2} + 1} }}\\ = {{ - x} \over {\sqrt {{x^2} + 1} }}.{1 \over {{{\sin }^2}\sqrt {{x^2} + 1} }}$

c) $y' = 3{\tan ^2}x\left( {\tan x} \right)' + \left( {2x} \right)'.\dfrac{{ - 1}}{{{{\sin }^2}2x}}$

$= 3{\tan ^2}x.\dfrac{1}{{{{\cos }^2}x}} - \dfrac{2}{{{{\sin }^2}2x}}\\ = {{3{{\tan }^2}x} \over {{{\cos }^2}x}} - {2 \over {{{\sin }^2}2x}}$

d) $y' = \left( {3x} \right)'.\dfrac{1}{{{{\cos }^2}3x}} - \left( {3x} \right)'.\dfrac{{ - 1}}{{{{\sin }^2}3x}}$

$= {3 \over {{{\cos }^2}3x}} + {3 \over {{{\sin }^2}3x}} \\= {{12} \over {{{\sin }^2}6x}}$

e) $y' = \left( {1 + 2\tan x} \right)'.\dfrac{1}{{2\sqrt {1 + 2\tan x} }}$

$= 2\left( {\tan x} \right)'.\dfrac{1}{{2\sqrt {1 + 2\tan x} }}\\ = \dfrac{1}{{{{\cos }^2}x}}.\dfrac{1}{{\sqrt {1 + 2\tan x} }}\\ = {1 \over {{\sqrt {1 + 2\tan x}.{\cos }^2}x }}$

f) $y' = x'\cot x + x.\left( {\cot x} \right)'$

$= \cot x + x.\dfrac{{ - 1}}{{{{\sin }^2}x}}\\= \cot x - {x \over {{{\sin }^2}x}}$

Chứng minh rằng:

a) Hàm số y = tanx thỏa mãn hệ thức $y' - {y^2} - 1 = 0$.

b) Hàm số y = cot2x thỏa mãn hệ thức $y' + 2{y^2} + 2 = 0$

Phương pháp giải:

Tính y' rồi thay vào tính vế trái của các đẳng thức, kiểm tra bằng vế phải và kết luận.

Hướng dẫn giải:

a) $y' = \dfrac{1}{{{{\cos }^2}x}} = 1 + {\tan ^2}x$

Do đó $y' - {y^2} - 1= \left( {1 + {{\tan }^2}x} \right) - {\tan ^2}x - 1 = 0$

b) $y' = \left( {2x} \right)'.\dfrac{{ - 1}}{{{{\sin }^2}2x}}$

= $- 2.\dfrac{1}{{{{\sin }^2}2x}} = - 2\left( {1 + {{\cot }^2}2x} \right).$

Do đó $y' + 2{y^2} + 2= - 2\left( {1 + {{\cot }^2}2x} \right) + 2{\cot ^2}2x + 2 = 0$

Tìm đạo hàm của mỗi hàm số sau:

a) $\displaystyle y = {{\sin x} \over x} + {x \over {{\mathop{\rm sinx}\nolimits} }}$

b) $\displaystyle y = {{{{\sin }^2}x} \over {1 + \tan 2x}}$

c) $y = \tan \left( {\sin x} \right)$

d) $y = x\cot \left( {{x^2} - 1} \right)$

e) $y = {\cos ^2}\sqrt {{\pi \over 4} - 2x}$

f) $y = x\sqrt {\sin 3x}$

Phương pháp giải:

Sử dụng công thức đạo hàm hàm hợp và các công thức tính đạo hàm các hàm số sơ cấp:

$\left( {\dfrac{u}{v}} \right)' = \dfrac{{u'v - uv'}}{{{v^2}}}$

$\left( {\sin x} \right)' = \cos x\\\left( {\cos x} \right)' = - \sin x$

$\left( {\cos u} \right)' = -u'. \sin u$

$\left( {\tan u} \right)' = \dfrac{u'}{{{{\cos }^2}u}}$

$\left( {\sqrt u } \right)' = \dfrac{{u'}}{{2\sqrt u }}$

Hướng dẫn giải:

a) $y' = \dfrac{{\left( {\sin x} \right)'.x - \sin x.\left( {x'} \right)}}{{{x^2}}} + \dfrac{{x'\sin x - x.\left( {\sin x} \right)'}}{{{{\sin }^2}x}}$

$\eqalign{ & = {{x\cos x - \sin x} \over {{x^2}}} + {{\sin x - x\cos x} \over {{{\sin }^2}x}} \cr & = \left( {x\cos x - {\mathop{\rm sinx}\nolimits} } \right)\left( {{1 \over {{x^2}}} - {1 \over {{{\sin }^2}x}}} \right) \cr}$

b) $y' = \frac{{\left( {{{\sin }^2}x} \right)'.\left( {1 + \tan 2x} \right) - {{\sin }^2}x.\left( {1 + \tan 2x} \right)'}}{{{{\left( {1 + \tan 2x} \right)}^2}}}$

$\eqalign{ & y' = {{2\sin x\cos x\left( {1 + \tan 2x} \right) - {{\sin }^2}x.2\left( {1 + {{\tan }^2}2x} \right)} \over {{{\left( {1 + \tan 2x} \right)}^2}}} \cr & = {{\sin 2x} \over {\left( {1 + \tan 2x} \right)}} - {{2{{\sin }^2}x\left( {1 + {{\tan }^2}2x} \right)} \over {{{\left( {1 + \tan 2x} \right)}^2}}} \cr}$

c) $y' = \left( {\sin x} \right)'.\dfrac{1}{{{{\cos }^2}\left( {\sin x} \right)}}$

$= {{\cos x} \over {{{\cos }^2}\left( {\sin x} \right)}}$

d) $y' = x'.\cot \left( {{x^2} - 1} \right) + x.\left[ {\cot \left( {{x^2} - 1} \right)} \right]'$

$= \cot \left( {{x^2} - 1} \right) + x.\left( {{x^2} - 1} \right)'.\dfrac{{ - 1}}{{{{\sin }^2}\left( {{x^2} - 1} \right)}}$

$\eqalign{ & = \cot \left( {{x^2} - 1} \right) + x.{{ - 2x} \over {{{\sin }^2}\left( {{x^2} - 1} \right)}} \cr & = \cot \left( {{x^2} - 1} \right) - {{2{x^2}} \over {{{\sin }^2}\left( {{x^2} - 1} \right)}} \cr}$

e) $y = {1 \over 2}\left( {1 + \cos 2\sqrt {{\pi \over 4} - 2x} } \right)$

$y' = - {1 \over 2}. \sin 2\sqrt {{\pi \over 4} - 2x} .\,2{{ - 2} \over {2\sqrt {{\pi \over 4} - 2x} }} \\= {{2\sin \sqrt {\pi - 8x} } \over {\sqrt {\pi - 8x} }}$

f) $y' = x'\sqrt {\sin 3x} + x.\left( {\sqrt {\sin 3x} } \right)'$

$= \sqrt {\sin 3x} + x.\dfrac{{\left( {\sin 3x} \right)'}}{{2\sqrt {\sin 3x}}}$

$= \sqrt {\sin 3x} + x.{{3\cos 3x} \over {2\sqrt {\sin 3x} }} \\= {{2\sin 3x + 3x\cos 3x} \over {2\sqrt {\sin 3x} }}$

Tính $f'\left( \pi \right)$ nếu $f\left( x \right) = {{\sin x - x\cos x} \over {\cos x - x\sin x}}$.

Phương pháp giải:

Sử dụng công thức tính đạo hàm:

$\left( {\frac{u}{v}} \right)' = \dfrac{{u'v - uv'}}{{{v^2}}}$

$\left( {\sin x} \right)' = \cos x\\\left( {\cos x} \right)' = - \sin x$

$u.v=u'v+uv'$

Hướng dẫn giải:

Với mọi x sao cho $\cos x - x\sin x \ne 0,$ ta có:

$f'\left( x \right) = {{\left[ {\cos x - \left( {\cos x - x\sin x} \right)} \right]\left( {\cos x - x\sin x} \right) - \left( {\sin x - x\cos x} \right)\left[ { - \sin x - \left( {\sin x + x\cos x} \right)} \right]} \over {{{\left( {{\mathop{\rm cosx}\nolimits} - xsinx} \right)}^2}}}$

Vì $\sin \pi = 0,\cos \pi = - 1$ nên:

$f'\left( \pi \right) = {{\left[ { - 1 - \left( { - 1} \right)} \right].\left( { - 1} \right) - \pi .\pi } \over {{{\left( { - 1} \right)}^2}}} = - {\pi ^2}$

Giải phương trình y’ = 0 trong mỗi trường hợp sau:

a) y = sin2x - 2cosx

b) y = 3sin2x + 4cos2x + 10x

c) $y = {\cos ^2}x + \sin x$

d) y = tan x + cot x

Phương pháp giải:

- Tính y' bằng cách sử dụng các công thức:

$\left( {\sin x} \right)' = \cos x\\\left( {\cos x} \right)' = - \sin x$                       $\left( {\sin u} \right)' =u'. \cos u\\\left( {\cos u} \right)' = -u' \sin u$

$\left( {\tan x} \right)' = \dfrac{1}{{{{\cos }^2}x}}$                       $\left( {\cot x} \right)' = - \dfrac{1}{{{{\sin }^2}x}}$

- Giải phương trình y' = 0 và kết luận nghiệm.

Hướng dẫn giải:

a) Với mọi $x \in\mathbb R$, ta có:

$y' = 2\cos 2x + 2\sin x$ $= 2\left( {1 - 2{{\sin }^2}x} \right) + 2\sin x$ $=-4{{\sin }^2}x+2\sin x+2$

Vậy $y' = 0 \Leftrightarrow 2{\sin ^2}x - \sin x - 1 = 0$

$\Leftrightarrow \left[ {\matrix{ {\sin x = 1} \cr {\sin x = -{1 \over 2}} \cr } } \right.$ $\Leftrightarrow \left[ {\matrix{ {x = {\pi \over 2} + k2\pi } \cr {x = - {\pi \over 6} + k2\pi } \cr {x = {{7\pi } \over 6} + k2\pi } \cr }\left( {k \in \mathbb Z} \right) } \right.$

b) Với mọi $x \in\mathbb R$, ta có: $y' = 6\cos 2x - 8\sin 2x + 10$

$y' = 0\\ \Leftrightarrow 6\cos 2x - 8\sin 2x + 10 = 0 \\\Leftrightarrow 3\cos 2x - 4\sin 2x + 5 = 0\\ \Leftrightarrow 4\sin 2x - 3\cos 2x = 5\\\Leftrightarrow {4 \over 5}\sin 2x - {3 \over 5}\cos 2x = 1\,\,\left( 1 \right)$

Vì ${\left( {{4 \over 5}} \right)^2} + {\left( {{3 \over 5}} \right)^2} = 1$ nên có số α sao cho $\cos \alpha = {4 \over 5}\,\text{ và }\,\sin \alpha = {3 \over 5}$

Thay vào (1), ta được:

$\eqalign{ & \sin 2x\cos \alpha - \sin\alpha \cos 2x = 1 \cr & \Leftrightarrow \sin \left( {2x - \alpha } \right) = 1 \cr & \Leftrightarrow 2x - \alpha = {\pi \over 2} + k2\pi \cr & \Leftrightarrow x = {1 \over 2}\left( {\alpha + {\pi \over 2} + k2\pi } \right)\,\,\left( {k \in\mathbb Z} \right) \cr}$

c) Với mọi $x \in\mathbb R$, ta có: $y' = - 2\cos x{\mathop{\rm sinx}\nolimits} + cosx = cosx\left( {1 - 2\sin x} \right)$

$\eqalign{ & y' = 0 \Leftrightarrow \cos x\left( {1 - 2\sin x} \right) = 0\cr & \Leftrightarrow \left[ {\matrix{ { \cos x = 0 } \cr {1 - 2\sin x = 0 } \cr } } \right. \cr & \Leftrightarrow \left[ {\matrix{ {x = {\pi \over 2} + k\pi} \cr {{\mathop{\rm sinx}\nolimits} = {1 \over 2} \Leftrightarrow \left[ {\matrix{ {x = {\pi \over 6} + k2\pi } \cr {x = {{5\pi } \over 6} + k2\pi } \cr } } \right. } \cr } } \right. \cr}$

Vậy $x = {\pi \over 2} + k\pi ;x = {\pi \over 6} + k2\pi ;x = {{5\pi } \over 6} + k2\pi \left( {k \in\mathbb Z} \right)$

d) Ta có:

$\eqalign{ & y' = {1 \over {{{\cos }^2}x}} - {1 \over {{{\sin }^2}x}}\,\forall\,x \ne k{\pi \over 2} \cr & y' = 0 \Leftrightarrow {1 \over {{{\cos }^2}x}} = {1 \over {{{\sin }^2}x}} \cr & \Leftrightarrow {\sin ^2}x = {\cos ^2}x\cr &\Leftrightarrow {\tan ^2}x = 1 \cr & \Leftrightarrow \tan x = \pm 1 \cr & \Leftrightarrow x = \pm {\pi \over 4} + k\pi,\ k \in \mathbb Z \cr}$

Cho hàm số $f\left( x \right) = 2{\cos ^2}\left( {4x - 1} \right)$. Chứng minh rằng với mọi x ta có $\left| {f'\left( x \right)} \right| \le 8.$ Tìm các giá trị của x để đẳng thức xảy ra.

Phương pháp giải:

Tính f'(x) và đánh giá sử dụng tính chất của hàm số lượng giác.

Hướng dẫn giải:

Với mọi $x \in\mathbb R$, ta có:

$f'\left( x \right) = 2.2\cos \left( {4x - 1} \right).\left[ { - \sin \left( {4x - 1} \right)} \right]4\\ = - 8\sin 2\left( {4x - 1} \right)$

Suy ra: $\left| {f'\left( x \right)} \right| = 8\left| {\sin 2\left( {4x - 1} \right)} \right| \le 8$

Dấu đẳng thức xảy ra khi và chỉ khi:

$\eqalign{ & \sin 2\left( {4x - 1} \right) = \pm 1 \cr & \Leftrightarrow 2\left( {4x - 1} \right) = {\pi \over 2} + k\pi \cr & \Leftrightarrow x = {\pi \over 16} + {{k\pi } \over 8} + {1 \over 4} \cr & \Leftrightarrow x = {1 \over {16}}\left( {\pi + 4 + k2\pi } \right)\,\,\left( {k \in\mathbb Z} \right) \cr}$

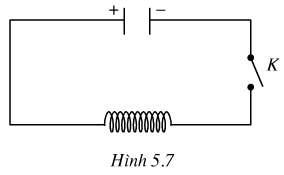
Cho mạch điện như hình 5.7. Lúc đầu tụ điện có điện tích Q₀. Khi đóng khóa K, tụ điện phóng điện qua cuộn dây; điện tích q của tụ điện phụ thuộc vào thời gian t theo công thức $q\left( t \right) = {Q_0}\sin \omega t.$ Trong đó, ω là tốc độ góc. Biết rằng cường độ $I(t)$ của dòng điện tại thời điểm t được tính theo công thức $I\left( t \right) = q'\left( t \right).$ Cho biết ${Q_0} = {10^{ - 8}}\,\text{ và }\,\omega = {10^6}\pi \,rad/s.$ Hãy tính cường độ của dòng điện tại thời điểm t = 6s (tính chính xác đến 10^-5 mA)

Phương pháp giải:

- Tính đạo hàm của q(t).

- Thay t = 6 vào I(t) và kết luận.

Hướng dẫn giải:

Cường độ dòng điện tại thời điểm t là:

$I\left( t \right) = q'\left( t \right) = {Q_0}\omega \cos \omega t$

Khi ${Q_0} = {10^{ - 8}}C\,\text{ và }\,\omega = {10^6}\pi \,rad/s$ thì cường độ dòng điện tại thời điểm t = 6s là:

$I\left( 6 \right) = {10^{ - 8}}{.10^6}\pi .\cos \left( {{{10}^6}\pi .6} \right)$ $= {\pi \over {100}}\left( A \right) \approx 31,41593\,\left( {mA} \right)$

Cho hàm số $y = {\cos ^2}x + m\sin x$ (m là tham số) có đồ thị là (C). Tìm m trong mỗi trường hợp sau:

a) Tiếp tuyến của (C) tại điểm với hoành độ x = π có hệ số góc bằng 1.

b) Hai tiếp tuyến của (C) tại các điểm có hoành độ $x = - {\pi \over 4}$ và $x = {\pi \over 3}$ song song hoặc trùng nhau.

Phương pháp giải:

a) Giải phương trình $f'(\pi )=1$ tìm m.

b) Giải phương trình $f'\left( { - {\pi \over 4}} \right) = f'\left( {{\pi \over 3}} \right)$ tìm m.

Hướng dẫn giải:

a) Đặt $f\left( x \right) = {\cos ^2}x + m\sin x,$ ta có :

$f'\left( x \right) = 2\cos x\left( { - \sin x} \right) + m\cos x$ $= - \sin 2x + m\cos x$

Hệ số góc tiếp tuyến của (C) tại điểm có hoành độ x = π là:

$\eqalign{ & f'\left( \pi \right) = - \sin 2\pi + m\cos \pi = - m \cr & \text{Vậy}\,f'\left( \pi \right) = 1 \Leftrightarrow m = - 1 \cr}$

b) Theo đề bài, ta có:

$\eqalign{ & f'\left( { - {\pi \over 4}} \right) = f'\left( {{\pi \over 3}} \right) \cr & \Leftrightarrow - \sin \left( { - {\pi \over 2}} \right) + m\cos \left( { - {\pi \over 4}} \right) \cr &= - \sin {{2\pi } \over 3} + m\cos {\pi \over 3} \cr & \Leftrightarrow 1 + m{{\sqrt 2 } \over 2} = - {{\sqrt 3 } \over 2} + {m \over 2} \cr &\Leftrightarrow m = {{\sqrt 3 + 2} \over {1 - \sqrt 2 }} \cr}$