Giải bài tập SGK Toán 11 Nâng cao Bài 3: Một số dạng phương trình lượng giác cơ bản

Giải các phương trình sau:

a) \(2\cos x - \sqrt 3 = 0\)

b) \(\sqrt 3 \tan 3x - 3 = 0\)

c) \(\left( {\sin x + 1} \right)\left( {2\cos 2x - \sqrt 2 } \right) = 0\)

Phương pháp giải:

a) Đưa phương trình về dạng cosx = a:

- Nếu |a| > 1 phương trình vô nghiệm.

- Nếu |a| ≤ 1 khi đó phương trình có nghiệm là: \(x=\pm\arccos a+k2\pi ,k \in \mathbb{Z}\)

b) - Đưa phương trình về dạng tan x = a.

- Phương trình tan x = a có nghiện là \(x=\arctan a+k\pi ,k \in \mathbb{Z}\)

c) Phương trình \(A.B = 0 \Leftrightarrow \left[ \begin{array}{l} A = 0\\ B = 0 \end{array} \right.\)

Hướng dẫn giải:

a) \(2\cos x - \sqrt 3 = 0\)

\( \Leftrightarrow \cos x = {{\sqrt 3 } \over 2} \\\Leftrightarrow \cos x = \cos {\pi \over 6} \\ \Leftrightarrow x = \pm {\pi \over 6} + k2\pi ,k \in\mathbb Z\)

b) \(\sqrt 3 \tan 3x - 3 = 0\)

\(\Leftrightarrow \tan 3x = \sqrt 3 \\ \Leftrightarrow \tan 3x = \tan {\pi \over 3} \\ \Leftrightarrow 3x = {\pi \over 3} + k\pi \\\Leftrightarrow x = {\pi \over 9} + k{\pi \over 3};k \in\mathbb Z \)

c)

\(\eqalign{& \left( {\sin x + 1} \right)\left( {2\cos 2x - \sqrt 2 } \right) = 0 \cr & \Leftrightarrow \left[ {\matrix{{\sin x + 1 = 0} \cr {2\cos 2x - \sqrt 2 = 0} \cr} } \right. \Leftrightarrow \left[ {\matrix{{\sin x = - 1} \cr {\cos 2x = {{\sqrt 2 } \over 2}} \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{x = - {\pi \over 2} + k2\pi } \cr {2x = \pm {\pi \over 4} + k2\pi } \cr} } \right. \Leftrightarrow \left[ {\matrix{{x = - {\pi \over 2} + k2\pi } \cr {2x = \pm {\pi \over 8} + k\pi } \cr} } \right. \cr}\)

Giải các phương trình sau:

a) \(2{\cos ^2}x - 3\cos x + 1 = 0\)

b) \({\cos ^2}x + \sin x + 1 = 0\)

c) \(\sqrt 3 {\tan ^2}x - \left( {1 + \sqrt 3 } \right)\tan x + 1 = 0\)

Phương pháp giải:

a) - Đặt t = cos x đưa về phương trình bậc hai ẩn t

- Giải phương trình bậc hai ẩn t sau đó giải các phương trình lượng giác cơ bản của cos.

b) - Sử dụng công thức: \({\sin ^2}x + {\cos ^2}x = 1\).

- Giải phương trình bậc hai ẩn sinx sau đó giải các phương trình lượng giác cơ bản của sin.

c) Giải phương trình bậc hai ẩn tanx sau đó giải các phương trình lượng giác cơ bản của tan.

Hướng dẫn giải:

a) Đặt t = cos x, \(|t| ≤ 1\) ta có:

\(2{t^2} - 3t + 1 = 0 \\ \Leftrightarrow \left[ {\matrix{{t = 1} \cr {t = {1 \over 2}} \cr} } \right. \Leftrightarrow \left[ {\matrix{{\cos x = 1} \cr {\cos x = {1 \over 2}} \cr} } \right. \\ \Leftrightarrow \left[ {\matrix{{x = k2\pi } \cr {x = \pm {\pi \over 3} + k2\pi } \cr} \left( {k \in\mathbb Z} \right)} \right.\)

b) Ta có:

\({\cos ^2}x + \sin x + 1 = 0 \\ \Leftrightarrow 1 - {\sin ^2}x + \sin x + 1 = 0 \\ \Leftrightarrow {\sin ^2}x - \sin x - 2 = 0 \\\Leftrightarrow \left[ {\matrix{{\sin x = - 1} \cr {\sin x = 2\,\left( {\text {loại }} \right)} \cr} } \right.\\ \Leftrightarrow x = - {\pi \over 2} + k2\pi \)

c) \(\sqrt 3 {\tan ^2}x - \left( {1 + \sqrt 3 } \right)\tan x + 1 = 0\)

\( \Leftrightarrow \left[ {\matrix{{\tan x = 1} \cr {\tan x = {1 \over {\sqrt 3 }}} \cr} } \right. \\ \Leftrightarrow \left[ {\matrix{{x = {\pi \over 4} + k\pi } \cr {x = {\pi \over 6} + k\pi } \cr} } \right.\left( {k \in\mathbb Z} \right)\)

Giải các phương trình sau trên khoảng đã cho rồi dùng bảng số hoặc máy tính bỏ túi để tính gần đúng nghiệm của chúng (tính chính xác đến hàng phần trăm):

a) \(3\cos 2x + 10\sin x + 1 = 0\) trên \(\left( { - {\pi \over 2};{\pi \over 2}} \right)\)

b) \(4\cos 2x + 3 = 0\) trên \(\left( {0;{\pi \over 2}} \right)\)

c) \({\cot ^2}x - 3\cot x - 10 = 0\) trên \(\left( {0;\pi } \right)\)

d) \(5 - 3\tan 3x = 0\) trên \(\left( { - {\pi \over 6};{\pi \over 6}} \right)\)

Phương pháp giải:

a) - Sử dụng công thức nhân đôi \(\cos 2x = 1 - 2{\sin ^2}x\).

- Giải phương trình bậc hai ẩn sinx sau đó giải các phương trình lượng giác cơ bản của sin.

- Dùng máy tính bỏ túi để tính gần đúng nghiệm của phương trình.

b) - Chuyển vế và giải phương trình cơ bản của cos.

- Dùng máy tính bỏ túi để tính gần đúng nghiệm của phương trình.

c) - Giải phương trình bậc hai ẩn cot x.

- Giải các phương trình lượng giác cơ bản của cot.

- Dùng máy tính bỏ túi để tính gần đúng nghiệm của phương trình.

d) - Chuyển vế và giải phương trình cơ bản của tan.

- Dùng máy tính bỏ túi để tính gần đúng nghiệm của phương trình.

Hướng dẫn giải:

a) Ta có:

\(3\cos 2x + 10\sin x + 1 = 0 \\ \Leftrightarrow - 6{\sin ^2}x + 6\sin x + 4 = 0 \\ \Leftrightarrow \left[ {\matrix{{\sin x = - {1 \over 3}} \cr {\sin x = 2\,\left( {\text{ loại }} \right)} \cr} } \right. \)

Phương trình \(\sin x = - {1 \over 3}\) có nghiệm gần đúng là \(x ≈ -0,34\)

b) Ta thấy \(0 < x < {\pi \over 2} \Leftrightarrow 0 < 2\pi < \pi .\)

 Với điều kiện đó, ta có:

\(4\cos 2x + 3 = 0\\ \Leftrightarrow \cos 2x = - {3 \over 4}\\ \Leftrightarrow 2x = \alpha\\ \Leftrightarrow x = {\alpha \over 2}\)

Trong đó α là số thực thuộc khoảng (0; π) thỏa mãn \(\cos \alpha = - {3 \over 4}\).

Dùng bảng số hoặc máy tính, ta tìm được \(α ≈ 2,42\).

Từ đó nghiệm gần đúng của phương trình là \(x = {\alpha \over 2} \approx 1,21\)

c) \({\cot ^2}x - 3\cot x - 10 = 0 \Leftrightarrow \left[ {\matrix{{\cot x = 5} \cr {\cot x = - 2} \cr} } \right.\)

Nghiệm gần đúng của phương trình trong khoảng (0; π) là \(x ≈ 0,2; x ≈ 2,68\)

d) \(x \in \left( { - {\pi \over 6};{\pi \over 6}} \right) \Leftrightarrow 3x \in \left( { - {\pi \over 2};{\pi \over 2}} \right)\)

Với điều kiện đó, ta có:

\(5 - 3\tan 3x = 0\\ \Leftrightarrow \tan 3x = {5 \over 3}\\ \Leftrightarrow 3x = \beta \\\Leftrightarrow x = {\beta \over 3}\)

Trong đó β là số thực thuộc khoảng \(\left( { - {\pi \over 2};{\pi \over 2}} \right)\) thỏa mãn \(\tan \beta = {5 \over 3};\) bảng số hoặc máy tính cho ta \(β ≈ 1,03\).

Vậy nghiệm gần đúng của phương trình là \(x ≈ 0,34\).

Giải các phương trình sau:

a) \(3\cos x + 4\sin x = -5\)

b) \(2\sin2x – 2\cos2x = \sqrt 2\)

c) \(5\sin2x – 6\cos^2 x = 13\)

Phương pháp giải:

a) Phương trình dạng asinx + bcosx = c:

- Chia hai vế phương trình cho \(\sqrt{a^2+b^2}\)

- Biến đổi VT phương trình về dạng \(a\sin x+b\cos x=\sqrt{a^2+b^2}\sin(x+\alpha)\)

trong đó \(\cos \alpha=\dfrac{a}{\sqrt{a^2+b^2}},\sin \alpha=\dfrac{b}{\sqrt{a^2+b^2}}\)

→ Phương trình trở thành phương trình bậc nhất đối với một hàm số lượng giác.

- Sử dụng công thức cos(a − b) = cosacosb + sinasinb để thu gọn phương trình.

b) c) Phương trình dạng asinx + bcosx = c:

- Chia hai vế phương trình cho \(\sqrt{a^2+b^2}\)

- Biến đổi VT phương trình về dạng \(a\sin x+b\cos x=\sqrt{a^2+b^2}\sin(x+\alpha)\)

trong đó \(\cos \alpha=\dfrac{a}{\sqrt{a^2+b^2}},\sin \alpha=\dfrac{b}{\sqrt{a^2+b^2}}\)

→ Phương trình trở thành phương trình bậc nhất đối với một hàm số lượng giác.

- Sử dụng công thức cos(a − b) = cosacosb + sinasinb để thu gọn phương trình.

- Sử dụng công thức sin(a+b) = sinacosb + cosasinb để thu gọn phương trình.

Hướng dẫn giải:

a) \(3\cos x + 4\sin x = -5\)

Chia hai vế phương trình cho \(\sqrt {{3^2} + {4^2}} = 5\) ta được:

\(\eqalign{ & {3 \over 5}\cos x + {4 \over 5}\sin x = - 1 \Leftrightarrow \cos x\cos \alpha + \sin x\sin \alpha = - 1 \cr & \left( {\text{ trong đó }\,\cos \alpha = {3 \over 5}\text { và }\,\sin \alpha = {4 \over 5}} \right) \cr & \text{ Ta có }\,:\,\cos \left( {x - \alpha } \right) = - 1 \Leftrightarrow x - \alpha = \pi + k2\pi \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow x = \pi + \alpha + k2\pi ,k \in Z \cr}\)

b) \(2\sin2x – 2\cos2x = \sqrt 2\)

Chia hai vế phương trình cho \(\sqrt {{2^2} + {2^2}} = 2\sqrt 2\) ta được:

\({1 \over {\sqrt 2 }}\sin 2x - {1 \over {\sqrt 2 }}\cos 2x = {1 \over 2} \\\Leftrightarrow \sin 2x\cos {\pi \over 4} - \cos 2x\sin {\pi \over 4} = {1 \over 2} \\\Leftrightarrow \sin \left( {2x - {\pi \over 4}} \right) = {1 \over 2} \\\Leftrightarrow \left[ {\matrix{{2x - {\pi \over 4} = {\pi \over 6} + k2\pi } \cr {2x - {\pi \over 4} = \pi - {\pi \over 6} + k2\pi } \cr} } \right. \\\Leftrightarrow \left[ {\matrix{{x = {{5\pi } \over {24}} + k\pi } \cr {x = {{13\pi } \over {24}} + k\pi } \cr} } \right.,k \in \mathbb Z\)

c) Ta có:

\(5\sin 2x - 6{\cos ^2}x = 13 \\ \Leftrightarrow 5\sin 2x - 3\left( {1 + \cos 2x} \right) = 13 \\\Leftrightarrow 5\sin 2x - 3\cos 2x = 16\)

Chia cả hai vế cho \(\sqrt {{5^2} - {3^2}} = \sqrt {34}\) ta được:

\({5 \over {\sqrt {34} }}\sin 2x - {3 \over {\sqrt {34} }}\cos 2x = {{16} \over {\sqrt {34} }}\)

Do \({\left( {{5 \over {\sqrt {34} }}} \right)^2} + {\left( {{3 \over {\sqrt {34} }}} \right)^2} = 1\) nên ta chọn được số α sao cho:

\(\cos \alpha = {5 \over {\sqrt {34} }}\,\text{ và }\,\sin \alpha = {3 \over {\sqrt {34} }}\)

Ta có:

\(5\sin 2x - 6{\cos ^2}x = 13 \\ \Leftrightarrow \sin \left( {2x - \alpha } \right) = {{16} \over {\sqrt {34} }} > 1\)

Vậy phương trình đã cho vô nghiệm. 

Một vật nặng treo bởi một chiếc lò xo, chuyển động lên xuống qua vị trí cân bằng.

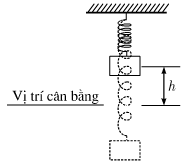
Khoảng cách h từ vật đó đến vị trí cân bằng ở thời điểm t giây được tính theo công thức h = |d| trong đó

\(d = 5\sin6t – 4\cos6t\)

với d được tính bằng xentimet, ta quy ước rằng d > 0 khi vật ở phía trên vị trí cân bằng, d < 0 khi vật ở phía dưới vị trí cân bằng. Hỏi:

a) Ở thời điểm nào trong 1 giây đầu tiên, vật ở vị trí cân bằng?

b) Ở thời điểm nào trong 1 giây đầu tiên, vật ở xa vị trí cân bằng nhất ?

(Tính chính xác đến \(\dfrac1{100}\) giây).

Phương pháp giải:

a) - Vật ở vị trí cân bằng khi d = 0.

- Giải phương trình sin(6t – α) = 0 để tìm t và kết luận.

b) - Vật ở xa vị trí cân bằng nhất khi và chỉ khi |d| nhận giá trị lớn nhất.

- Giải phương trình \(\sin(6t – α) = ± 1\)và kết luận.

Hướng dẫn giải:

a) Ta có:

\(5\sin 6t - 4cos6t \\= \sqrt {41} \left( {{5 \over {\sqrt {41} }}\sin 6t - {4 \over {\sqrt {41} }}\cos 6t} \right) \\= \sqrt {41} \sin \left( {6t - \alpha } \right)\)

Trong đó số α được chọn sao cho \(\cos \alpha = {5 \over {\sqrt {41} }}\,\text{ và }\,\sin \alpha = {4 \over {\sqrt {41} .}}\).

Sử dụng bảng số hoặc máy tính bỏ túi, ta chọn được \(α ≈ 0,675\)

Vật ở vị trí cân bằng khi d = 0, nghĩa là sin(6t – α) = 0

\(\Leftrightarrow t = {\alpha \over 6} + k{\pi \over 6}\)

Ta cần tìm k nguyên dương sao cho 0 ≤ t ≤ 1

\(0 ≤ t ≤ 1 ⇔ 0 \le {\alpha \over 6} + k{\pi \over 6} \le 1 \Leftrightarrow - {\alpha \over \pi } \le k \le {{6 - \alpha } \over \pi }\)

Vậy trong khoảng 1 giây đầu tiên, có hai thời điểm vật ở vị trí cân bằng là:

\(t \approx {\alpha \over 6} \approx 0,11\) (giây) và \(t = {\alpha \over 6} + {\pi \over 6} \approx 0,64\) (giây)

b) Vật ở xa vị trí cân bằng nhất khi và chỉ khi |d| nhận giá trị lớn nhất.

Điều đó xảy ra nếu \(\sin(6t – α) = ± 1\)

Ta có:

\(\sin \left( {6t - \alpha } \right) = \pm 1\\ \Leftrightarrow \cos \left( {6t - \alpha } \right) = 0\\ \Leftrightarrow {\alpha \over 6} + {\pi \over {12}} + k{\pi \over 6}\)

Ta tìm k nguyên dương sao cho 0 ≤ t ≤ 1

\(\eqalign{ & 0 \le t \le 1 \Leftrightarrow 0 \le {\alpha \over 6} + {\pi \over {12}} + k{\pi \over 6} \le 1 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow - {\alpha \over \pi } - {1 \over 2} \le k \le {{6 - \alpha } \over \pi } - {1 \over 2} \cr}\)

Vậy trong khoảng 1 giây đầu tiên, có hai thời điểm vật ở xa vị trí cân bằng nhất là:

\(t = {\alpha \over 6} + {\pi \over {12}} \approx 0,37\,\left( \text{giây} \right)\,\text{và}\,t = {\alpha \over 6} + {\pi \over {12}} + {\pi \over 6} \approx 0,90\,\left( \text{giây} \right)\)

Tìm giá trị lớn nhất và giá trị nhỏ nhất của mỗi biểu thức sau:

a) \(a\sin x + b\cos x\) (a và b là hằng số, \(a^2+ b^2≠ 0\))

b) \({\sin ^2}x + \sin x\cos x + 3{\cos ^2}x\)

c) \(A{\sin ^2}x + B\sin x\cos x + C{\cos ^2}x\) (A, B, C là hằng số)

Phương pháp giải:

a) Biến đổi biểu thức về dạng C.sin(x + t)

b) c) Sử dụng công thức hạn bậc:

\(\begin{array}{l} {\sin ^2}a = \frac{{1 - \cos 2a}}{2}\\ {\cos ^2}a = \frac{{1 + \cos 2a}}{2} \end{array}\)

Hướng dẫn giải:

a) Ta có:

\(\eqalign{ & a\sin x + b\cos x = \sqrt {{a^2} + {b^2}} \left( {{a \over {\sqrt {{a^2} + {b^2}} }}\sin x + {b \over {\sqrt {{a^2} + {b^2}} }}\cos x} \right) \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {{a^2} + {b^2}} \left( {\sin x\cos \alpha + \sin \alpha \cos x} \right) \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {{a^2} + {b^2}} \sin \left( {x + \alpha } \right) \cr & \left( {\text{ trong đó}\,\sin \alpha = {b \over {\sqrt {{a^2} + {b^2}} }};\,\cos \alpha = {a \over {\sqrt {{a^2} + {b^2}} }}} \right) \cr}\)

Giá trị lớn nhất và giá trị nhỏ nhất của asinx + bcosx lần lượt là:

\(\sqrt {{a^2} + {b^2}} \,\text{ và }\, - \sqrt {{a^2} + {b^2}}\)

b) Ta có:

\(\eqalign{ & {\sin ^2}x + \sin x\cos x + 3{\cos ^2}x = {1 \over 2}\sin 2x + {{1 - \cos 2x} \over 2} + 3.{{1 + \cos 2x} \over 2} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {1 \over 2}\sin 2x + \cos 2x + 2 \cr & \text{ Ta có }\,\left| {{1 \over 2}\sin 2x + \cos 2x} \right| \le \sqrt {{{\left( {{1 \over 2}} \right)}^2} + {1^2}} = {{\sqrt 5 } \over 2} \cr}\)

Do đó giá trị lớn nhất và giá trị nhỏ nhất của \({\sin ^2}x + \sin x\cos x + 3{\cos ^2}x\) lần lượt là:

\({{\sqrt 5 } \over 2} + 2\,\text{ và }\, - {{\sqrt 5 } \over 2} + 2\)

c) Ta có:

\(\eqalign{ & A{\sin ^2}x + B\sin x\cos x + C{\cos ^2}x \cr & = A.{{1 - \cos 2x} \over 2} + {B \over 2}.\sin 2x + C.{{1 + \cos 2x} \over 2} \cr & = {B \over 2}.\sin 2x + {{C - A} \over 2}\cos 2x + {{C + A} \over 2} = a\sin 2x + b\cos 2x + c \cr & \text{ trong đó}\,\,a = {B \over 2},\,b = {{C - A} \over 2},\,c = {{C + A} \over 2} \cr}\)

Vậy \(A{\sin ^2}x + B\sin x\cos x + C{\cos ^2}x\) đạt GTLN là:

\(\sqrt {{a^2} + {b^2}} + c = \sqrt {{{{B^2} + {{\left( {C - A} \right)}^2}} \over 4}} + {{C + A} \over 2} = {1 \over 2}\sqrt {{B^2} + \left( {C - A} \right)} + {{C + A} \over 2}\)

và đạt GTNN là \(- {1 \over 2}\sqrt {{B^2} + {{\left( {C - A} \right)}^2}} + {{C + A} \over 2}.\)

Giải các phương trình sau:

a) \(2{\sin ^2}x + 3\sqrt 3 \sin x\cos x - {\cos ^2}x = 4\)

b) \(3{\sin ^2}x + 4\sin 2x + \left( {8\sqrt 3 - 9} \right){\cos ^2}x = 0\)

c) \({\sin ^2}x + \sin 2x - 2{\cos ^2}x = {1 \over 2}\)

Phương pháp giải:

Phương pháp giải phương trình đẳng cấp đối với sin và cos:

\(a{\sin}^2 x+b\sin x\cos x+c{\cos}^2 x=d\)

- Bước 1: Xét cosx = 0 có là nghiệm của phương trình hay không?

- Bước 2: Khi cosx ≠ 0

+ Chia cả 2 vế của phương trình cho cos²x ta được: 

\(a\dfrac{{\sin}^2 x}{{\cos}^2 x}+b\dfrac{\sin x}{\cos x}+c=\dfrac{d}{{\cos}^2 x}\)

⇔ \(a{\tan}^2 x+b\tan x+c=d(1+{\tan}^2 x)\)

+ Giải phương trình lượng giác cơ bản của tan:

tanx = tanα ⇔ x = α + kπ, k ∈ Z và đối chiếu với điều kiện.

Hướng dẫn giải:

a) cos x = 0 không thỏa mãn phương trình.

Chia hai vế phương trình cho \({\cos ^2}x \ne 0\) ta được:

\(\eqalign{ & 2{\tan ^2}x + 3\sqrt 3 \tan x - 1 = 4\left( {1 + {{\tan }^2}x} \right) \cr & \Leftrightarrow 2{\tan ^2}x - 3\sqrt 3 \tan x + 5 = 0 \cr}\)

Phương trình vô nghiệm nên phương trình đã cho vô nghiệm.

b) Các giá trị của x mà cosx = 0 không là nghiệm phương trình.

Chia hai vế phương trình cho \({\cos ^2}x \ne 0\) ta được:

\(\eqalign{& 3{\tan ^2}x + 8\tan x + 8\sqrt 3 - 9 = 0 \Leftrightarrow \left[ {\matrix{{\tan x = - \sqrt 3 } \cr {\tan x = - {8 \over 3} + \sqrt 3 } \cr} } \right. \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\;\;\;\;\;\;\;\;\;\;\;\, \Leftrightarrow \left[ {\matrix{{x = {\pi \over 3} + k\pi } \cr {x = \alpha + k\pi } \cr} } \right.\,\,k \in\mathbb Z \cr & \,\,\,\,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\text{ trong đó}\,\tan \alpha = - {8 \over 3} + \sqrt 3 \cr}\)

c) Các giá trị của x mà cosx = 0 không là nghiệm phương trình.

Chia hai vế phương trình cho cos²x ta được:

\({\tan ^2}x + 2\tan x - 2 = {1 \over 2}\left( {1 + {{\tan }^2}x} \right) \\\Leftrightarrow {\tan ^2}x + 4\tan x - 5 = 0 \\ \Leftrightarrow \left[ {\matrix{{\tan x = 1} \cr {\tan x = - 5} \cr} } \right. \\\Leftrightarrow \left[ {\matrix{{x = {\pi \over 4} + k\pi } \cr {x = \alpha + k\pi } \cr} } \right. \)

Trong đó \(\tan \alpha=-5\).

Sử dụng công thức biến đổi tổng thành tích hoặc tích thành tổng để giải các phương trình sau:

a) \(\cos x\cos 5x = \cos 2x\cos 4x\)

b) \(\cos 5x\sin 4x=\cos 3x\sin 2x\)

c) \(\sin 2x + \sin 4x = \sin 6x\)

d) \(\sin x + \sin 2x = \cos x + \cos 2x\)

Phương pháp giải:

Sử dụng các công thức:

\(\sin a + \sin b = 2\sin \frac{{a + b}}{2}\cos \frac{{a - b}}{2}\)

\(\cos a + \cos b = 2\cos \frac{{a + b}}{2}\cos \frac{{a - b}}{2}\)

\(\cos a.\cos b = \frac{1}{2}\left[ {\cos (a + b) + \cos (a - b)} \right]\)

\(\sin a.\cos b = \frac{1}{2}\left[ {\sin (a + b) + \sin (a - b)} \right]\)

Hướng dẫn giải:

a) \(\cos x\cos 5x = \cos 2x\cos 4x\)

\(\Leftrightarrow {1 \over 2}\left( {\cos 6x + \cos 4x} \right) = {1 \over 2}\left( {\cos 6x + \cos 2x} \right) \)

\(\Leftrightarrow \cos 4x = \cos 2x \)

\(\Leftrightarrow \left[ {\matrix{{4x = 2x + k2\pi } \cr {4x = - 2x + k2\pi } \cr} } \right. \\ \Leftrightarrow \left[ {\matrix{{x = k\pi } \cr {x = k{\pi \over 3}} \cr} } \right. \\ \Leftrightarrow x = k{\pi \over 3} \,\,(k\in\mathbb Z)\)

b) \(\cos 5x\sin 4x=\cos 3x\sin 2x\)

\(\Leftrightarrow {1 \over 2}\left( {\sin 9x - \sin x} \right) = {1 \over 2}\left( {\sin 5x - \sin x} \right)\)

\(\Leftrightarrow \sin 9x = \sin 5x \\ \Leftrightarrow \left[ {\matrix{{9x = 5x + k2\pi } \cr {9x = \pi - 5x + k2\pi } \cr} } \right. \\ \Leftrightarrow \left[ {\matrix{{x = k{\pi \over 2}} \cr {x = {\pi \over {14}} + k{\pi \over 7}} \cr} } \,\,(k\in\mathbb Z) \right.\)

c) \(\sin 2x + \sin 4x = \sin 6x\)

\(\Leftrightarrow 2\sin 3x\cos x = 2\sin 3x\cos 3x\)

\(\Leftrightarrow \sin 3x\left( {\cos x - \cos 3x} \right) = 0 \\ \Leftrightarrow \left[ {\matrix{{\sin 3x = 0} \cr {\cos x = \cos 3x} \cr} } \right. \\ \Leftrightarrow \left[ {\matrix{{x = k{\pi \over 3}} \cr {x = k\pi } \cr {x = k{\pi \over 2}} \cr} } \right. \\ \Leftrightarrow \left[ {\matrix{{x = k{\pi \over 3}} \cr {x = k{\pi \over 2}} \cr} } \,\,(k\in\mathbb Z)\right. \)

d) \(\sin x + \sin 2x = \cos x + \cos 2x\)

\(\Leftrightarrow 2\sin {{3x} \over 2}\cos {x \over 2} = 2\cos {{3x} \over 2}\cos {x \over 2}\)

\(\Leftrightarrow \cos {x \over 2}\left( {\sin {{3x} \over 2} - \cos {{3x} \over 2}} \right) = 0 \\\Leftrightarrow \left[ {\matrix{{\cos {x \over 2} = 0} \cr {\sin {{3x} \over 2} = \cos {{3x} \over 2}} \cr} } \right.\)

\(\Leftrightarrow \left[ {\matrix{{{x \over 2} = {\pi \over 2} + k\pi } \cr {\tan {{3x} \over 2} = 1} \cr} } \right.\)

\(\Leftrightarrow \left[ {\matrix{{x = \pi + k2\pi } \cr {x = {\pi \over 6} + k{{2\pi } \over 3}} \cr} } \right.\left( {k \in\mathbb Z} \right)\)

Dùng công thức hạ bậc để giải các phương trình sau:

a) \({\sin ^2}4x + {\sin ^2}3x = {\sin ^2}2x + {\sin ^2}x\)

b) \({\cos ^2}x + {\cos ^2}2x + {\cos ^2}3x + {\cos ^2}4x = 2\)

Phương pháp giải:

Sử dụng công thức hạ bậc:

\(\begin{array}{l} {\sin ^2}a = \frac{{1 - \cos 2a}}{2}\\ {\cos ^2}a = \frac{{1 + \cos 2a}}{2} \end{array}\)

Hướng dẫn giải:

a) Ta có:

\(\eqalign{& {\sin ^2}4x + {\sin ^2}3x = {\sin ^2}2x + {\sin ^2}x \cr & \Leftrightarrow {1 \over 2}\left( {1 - \cos 8x} \right) + {1 \over 2}\left( {1 - \cos 6x} \right) = {1 \over 2}\left( {1 - \cos 4x} \right) + {1 \over2}\left( {1 - \cos 2x} \right) \cr & \Leftrightarrow \cos 8x + \cos 6x = \cos 4x + \cos 2x \cr & \Leftrightarrow \cos 7x\cos x = \cos 3x\cos x \cr & \Leftrightarrow \cos x\left( {\cos 7x - \cos 3x} \right) = 0 \cr & \Leftrightarrow \left[ {\matrix{{\cos x = 0} \cr {\cos 7x = \cos 3x} \cr} } \right. \Leftrightarrow \left[ {\matrix{{x = {\pi \over 2} + k\pi } \cr {x = k{\pi \over 2}} \cr {x = k{\pi \over 5}} \cr} } \right. \Leftrightarrow \left[ {\matrix{{x = k{\pi \over 2}} \cr {x = k{\pi \over 5}} \cr} } \right.\,\,\,k \in\mathbb Z \cr}\)

b) Ta có:

\(\eqalign{& {\cos ^2}x + {\cos ^2}2x + {\cos ^2}3x + {\cos ^2}4x = 2 \cr & \Leftrightarrow {{1 + \cos 2x} \over 2} + {{1 + \cos 4x} \over 2} + {{1 + \cos 6x} \over 2} + {{1 + \cos 8x} \over 2} = 2 \cr & \Leftrightarrow \left( {\cos 2x + \cos 4x} \right) + \left( {\cos 6x + \cos 8x} \right) = 0 \cr & \Leftrightarrow 2\cos 3x\cos x + 2\cos 7x\cos x = 0 \cr & \Leftrightarrow \cos x\left( {\cos 3x + \cos 7x} \right) = 0 \cr & \Leftrightarrow 2\cos x\cos 5x\cos 2x = 0 \Leftrightarrow \left[ {\matrix{{\cos x = 0} \cr {\cos 2x = 0} \cr {\cos 5x = 0} \cr} } \right. \Leftrightarrow \left[ {\matrix{{x = {\pi \over 2} + k\pi } \cr {x = {\pi \over 4} + k{\pi \over 2}} \cr {x = {\pi \over {10}} + k{\pi \over 5}} \cr} } \right.\,\,\left( {k \in\mathbb Z} \right) \cr}\)

Giải các phương trình sau:

a) \(\tan {x \over 2} = \tan x\)

b) \(\tan \left( {2x + 10^\circ } \right) + \cot x = 0\)

c) \(\left( {1 - \tan x} \right)\left( {1 + \sin 2x} \right) = 1 + \tan x\)

d) \(\tan x + \tan 2x = \sin 3x\cos x\)

e) \(\tan x + \cot 2x = 2\cot 4x\)

Phương pháp giải:

- Tìm ĐKXĐ.

- Sử dụng các công thức:

cot x = - tan (90^o + x)

\(\sin 2a = {{2\tan a} \over {1 + {{\tan }^2}a}}\)

\(\tan a + \tan b = \frac{{\sin (a + b)}}{{\cos a + \cos b}}\)

\({\cos ^2}a = \frac{{1 + \cos 2a}}{2}\)

cos (a + b) = cos a. cos b - sin a. sin b.

- Giải các phương trình lượng giác cơ bản của sin, cos, tan, cot.

Hướng dẫn giải:

a) \(\tan {x \over 2} = \tan x\)

ĐKXĐ: \(\left\{ {\matrix{{\cos {x \over 2} \ne 0} \cr {\cos x \ne 0} \cr} } \right.\)

Ta có:

\(\tan {x \over 2} = \tan x \Leftrightarrow x = {x \over 2} + k\pi\Leftrightarrow x = k2\pi \,\) (nhận).

b) \(\tan \left( {2x + 10^\circ } \right) + \cot x = 0\)

ĐKXĐ: \(\left\{ {\matrix{{\cos \left( {2x + 10^\circ } \right) \ne 0} \cr {\sin x \ne 0} \cr} } \right.\)

Ta có:

\( \tan \left( {2x + 10^\circ } \right) + \cot x = 0 \\\Leftrightarrow \tan \left( {2x + 10^\circ } \right) = \tan \left( {90^\circ + x} \right) \\ \Leftrightarrow 2x + 10^\circ = 90^\circ + x + k180^\circ \\ \Leftrightarrow x = 80^\circ + k180^\circ\)

c) \(\left( {1 - \tan x} \right)\left( {1 + \sin 2x} \right) = 1 + \tan x\)

Đặt t = tanx, với điều kiện cosx ≠ 0

Ta có: \(\sin 2x = {{2\tan x} \over {1 + {{\tan }^2}x}} = {{2t} \over {1 + {t^2}}}\)

Do đó \(1 + \sin 2x = 1 + {{2t} \over {1 + {t^2}}} = {{{{\left( {1 + t} \right)}^2}} \over {1 + {t^2}}}\)

Vậy ta có phương trình

\(\eqalign{& \left( {1 - t} \right){{{{\left( {1 + t} \right)}^2}} \over {1 + {t^2}}} = 1 + t \cr & \Leftrightarrow \left( {1 - t} \right){\left( {1 + t} \right)^2} = \left( {1 + t} \right)\left( {1 + {t^2}} \right)\Leftrightarrow 2{t^2}\left( {1 + t} \right) = 0 \cr & \Leftrightarrow \left[ {\matrix{{t = 0} \cr {t = - 1} \cr} } \right. \Leftrightarrow \left[ {\matrix{{\tan x = 0} \cr {\tan x = - 1} \cr} } \right. \Leftrightarrow \left[ {\matrix{{x = k\pi } \cr {x = - {\pi \over 4} + k\pi } \cr} } \right. \cr}\)

d) \(\tan x + \tan 2x = \sin 3x\cos x\)

ĐK: \(\cos x \ne 0\,\text{ và }\,\cos 2x \ne 0.\) Với điều kiện đó, ta có:

\(\eqalign{& \tan x + \tan 2x = \sin 3x\cos x \cr & \Leftrightarrow {{\sin 3x} \over {\cos x\cos 2x}} = \sin 3x\cos x \cr & \Leftrightarrow \sin 3x\left( {{1 \over {\cos x\cos 2x}} - \cos x} \right) = 0 \cr & \Leftrightarrow \left[ {\matrix{{\sin 3x = 0} \cr {{1 \over {\cos x\cos 2x}} = \cos x} \cr} } \right. \cr & .\sin 3x = 0 \Leftrightarrow x = k{\pi \over 3} \cr & .{1 \over {\cos x\cos 2x}} = \cos x \Leftrightarrow {\cos ^2}x\cos 2x = 1 \Leftrightarrow \left( {1 + \cos 2x} \right)\cos 2x = 2 \cr & \Leftrightarrow {\cos ^2}2x + \cos 2x - 2 = 0 \cr & \Leftrightarrow \cos 2x = 1 \Leftrightarrow x = k\pi \cr}\)

Vậy phương trình có nghiệm \(x = k{\pi \over 3}\left( {k \in \mathbb Z} \right)\)

e) \(\tan x + \cot 2x = 2\cot 4x\)

ĐKXĐ: \(\sin 4x ≠ 0\)

Với điều kiện đó ta có:

\(\eqalign{& \tan x + \cot 2x = 2\cot 4x \cr & \Leftrightarrow {{\sin x} \over {\cos x}} + {{\cos 2x} \over {\sin 2x}} = {{2\cos 4x} \over {\sin 4x}} \cr & \Leftrightarrow {{\sin x\sin 2x + \cos x\cos 2x} \over {\cos x\sin 2x}} = {{2\cos 4x} \over {2\sin 2x\cos 2x}} \cr & \Leftrightarrow {{\cos \left( {2x - x} \right)} \over {\cos x}} = {{\cos 4x} \over {\cos 2x}} \cr & \Leftrightarrow \cos 4x = \cos 2x \cr & \Leftrightarrow 4x = \pm 2x + k2\pi \Leftrightarrow \left[ {\matrix{{x = k\pi } \cr {x = k{\pi \over 3}} \cr} } \right. \Leftrightarrow x = k{\pi \over 3} \cr}\)

Vậy nghiệm của phương trình là \(x = k{\pi \over 3}\) với k nguyên và không chia hết cho 3.

Mùa xuân ở Hội Lim (tỉnh Bắc Ninh) thường có trò chơi đu. Khi người chơi đu nhún đều, cây đu sẽ đưa người chơi đu dao động qua lại vị trí cân bằng. Nghiên cứu trò chơi này, người ta thấy khoảng cách h (tính bằng mét) từ người chơi đu đến vị trí cân bằng được biểu diễn qua thời gian t (t ≥ 0 và được tính bằng giây) bởi hệ thức h = |d| với \(d = 3\cos \left[ {{\pi \over 3}\left( {2t - 1} \right)} \right]\), trong đó ta quy ước rằng d > 0 khi vị trí cân bằng ở về phía sau lưng người chơi đu và d < 0 trong trường hợp trái lại.

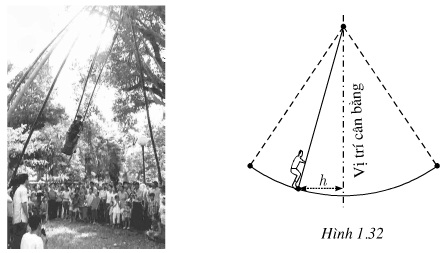
a) Tìm các thời điểm trong vòng 2 giây đầu tiên mà người chơi đu ở xa vị trí cân bằng nhất.

b) Tìm các thời điểm trong vòng 2 giây đầu tiên mà người chơi đu cách vị trí cân bằng 2 mét (tính chính xác đến \({1 \over {100}}\) giây).

Phương pháp giải:

a) - Người chơi đu ở xa vị trí cân bằng nhất khi \( \cos \left[ {{\pi \over 3}\left( {2t - 1} \right)} \right] = \pm 1\)

- Giải phương trình tìm t và kết luận.

b) - Người chơi đu cách vị trí cân bằng 2 mét khi \(3\cos \left[ {{\pi \over 3}\left( {2t - 1} \right)} \right] = \pm 2\)

- Giải phương trình tìm t và kết luận.

Hướng dẫn giải:

a) Người chơi đu ở xa vị trí cân bằng nhất khi \( \cos \left[ {{\pi \over 3}\left( {2t - 1} \right)} \right] = \pm 1\)

Ta có:

\(\eqalign{ & \cos \left[ {{\pi \over 3}\left( {2t - 1} \right)} \right] = \pm 1\cr& \Leftrightarrow \sin \left[ {{\pi \over 3}\left( {2t - 1} \right)} \right] = 0 \cr & \Leftrightarrow {\pi \over 3}\left( {2t - 1} \right) = k\pi\cr& \Leftrightarrow t = {1 \over 2}\left( {3k + 1} \right) \cr} \)

Ta cần tìm k nguyên để 0 ≤ t ≤ 2\)

\(0 \le t \le 2 \Leftrightarrow 0 \le {1 \over 2}\left( {3k + 1} \right) \le 2 \) \(\Leftrightarrow - {1 \over 3} \le k \le 1 \Leftrightarrow k \in \left\{ {0;1} \right\}\)

Với k = 0 thì \(t = {1 \over 2}.\)

Với k = 1 thì t = 2.

Vậy trong 2 giây đầu tiên, người chơi đu ở xa vị trí cân bằng nhất vào các thời điểm \({1 \over 2}\) giây và 2 giây.

b) Người chơi đu cách vị trí cân bằng 2 mét khi \(3\cos \left[ {{\pi \over 3}\left( {2t - 1} \right)} \right] = \pm 2\)

Ta có:

\(\eqalign{ & 3\cos \left[ {{\pi \over 3}\left( {2t - 1} \right)} \right] = \pm 2 \cr & \Leftrightarrow {\cos ^2}\left[ {{\pi \over 3}\left( {2t - 1} \right)} \right] = {4 \over 9} \cr & \Leftrightarrow \frac{{1 + \cos \left[ {\frac{{2\pi }}{3}\left( {2t - 1} \right)} \right]}}{2} = \frac{4}{9}\cr& \Leftrightarrow 1 + \cos \left[ {{{2\pi } \over 3}\left( {2t - 1} \right)} \right] = {8 \over 9} \cr & \Leftrightarrow \cos \left[ {{{2\pi } \over 3}\left( {2t - 1} \right)} \right] = - {1 \over 9} \cr & \Leftrightarrow {{2\pi } \over 3}\left( {2t - 1} \right) = \pm \alpha + k2\pi \cr & \Leftrightarrow t = \pm {{3\alpha } \over {4\pi }} + {1 \over 2} + {{3k} \over 2}\cr&\left( {\text{với}\,\cos \alpha = - {1 \over 9}} \right) \cr} \)

Ta tìm k nguyên để 0 ≤ t ≤ 2

- Với \(t = {{3\alpha } \over {4\pi }} + {1 \over 2} + {{3k} \over 2}\) ta có :

\(0 \le t \le 2 \Leftrightarrow - {1 \over 3} - {\alpha \over {2\pi }} \le k \le 1 - {\alpha \over {2\pi }}\)

Với \(\cos \alpha = - {1 \over 9}\) ta chọn α ≈ 1,682

Khi đó – 0,601 < k < 0,732 suy ra k = 0 và t ≈ 0,90

- Với \(t = - {{3\alpha } \over {4\pi }} + {1 \over 2} + {{3k} \over 2}\) ta có :

\(0 \le t \le 2 \Leftrightarrow - {1 \over 3} + {\alpha \over {2\pi }} \le k \le 1 + {\alpha \over {2\pi }}\)

Vì α ≈ 1,682 nên – 0,066 < k < 1,267, suy ra \(k \in {\rm{\{ }}0;1\} \)

Với k = 0, ta có t ≈ 0,10; với k = 1, ta có t ≈ 1,60

Kết luận: Trong khoảng 2 giây đầu tiên, có ba thời điểm mà người chơi đu cách vị trí cân bằng 2 mét, đó là t ≈ 0,10 giây; t ≈ 0,90 giây và t ≈ 1,60 giây.

Giải các phương trình sau:

a) \({\cos ^2}x - 3{\sin ^2}x = 0\)

b) \({\left( {\tan x + \cot x} \right)^2} - \left( {\tan x + \cot x} \right) = 2\)

c) \(\sin x + {\sin ^2}{x \over 2} = 0,5\)

Phương pháp giải:

a) Sử dụng công thứ hạ bậc để giải phương trình:

\(\begin{array}{l} {\sin ^2}\alpha = \dfrac{{1 - \cos 2\alpha}}{2}\\ {\cos ^2}\alpha = \dfrac{{1 + \cos 2\alpha }}{2} \end{array}\)

b) Đặt ẩn phụ \(t = \tan x + \cot x\) và giải phương trình.

c) Sử dụng công thứ hạ bậc để giải phương trình:

\({\sin ^2}\alpha = \dfrac{{1 - \cos 2\alpha}}{2}\)

Hướng dẫn giải:

a) Ta có:

\(\eqalign{ & {\cos ^2}x - 3{\sin ^2}x = 0 \cr & \Leftrightarrow {{1 + \cos 2x} \over 2} - {{3\left( {1 - \cos 2x} \right)} \over 2} = 0 \cr & \Leftrightarrow \cos 2x = {1 \over 2} \Leftrightarrow 2x = \pm {\pi \over 3} + k2\pi \cr & \Leftrightarrow x = \pm {\pi \over 6} + k\pi \cr}\)

b) \({\left( {\tan x + \cot x} \right)^2} - \left( {\tan x + \cot x} \right) = 2\)

Đặt t = tan x + cot x với điều kiện \(|t| = |\tan x| + |\cot x| ≥ 2\) (BĐT Côsi)

Ta có:

\(\eqalign{& {t^2} - t = 2 \Leftrightarrow {t^2} - t - 2 = 0 \Leftrightarrow \left[ {\matrix{{t = - 1\,\left( \text{loại} \right)} \cr {t = 2} \cr} } \right. \cr & t = 2 \Leftrightarrow \tan x + \cot x = 2 \Leftrightarrow \tan x = {1 \over {\tan x}} = 2 \cr & \Leftrightarrow {\tan ^2}x - 2\tan x + 1 = 0 \cr & \Leftrightarrow \tan x = 1 \Leftrightarrow x = {\pi \over 4} + k\pi \cr}\)

c) Ta có:

\(\eqalign{ & \sin x + {\sin ^2}{x \over 2} = 0,5 \cr & \Leftrightarrow \sin x + {{1 - \cos x} \over 2} = {1 \over 2} \Leftrightarrow \sin x = {1 \over 2}\cos x \cr & \Leftrightarrow \tan x = {1 \over 2} \Leftrightarrow x = \alpha + k\pi \,\text{ trong đó}\tan \alpha = {1 \over 2} \cr}\)

Chứng minh rằng các phương trình sau đây vô nghiệm:

a) \(\sin x – 2\cos x = 3\)

b) \(5\sin2x + \sin x + \cos x + 6 = 0\)

Phương pháp giải:

a) - Chia hai vế phương trình cho \(\sqrt5\)

- Sử dụng công thức sin(a + b) = sina.cosb + cosa.sinb

b) - Đặt t = sinx + cosx.

- Chứng minh phương trình theo t vô nghiệm.

⇒ Phương trình đã cho vô nghiệm.

Hướng dẫn giải:

a) \(\sin x – 2\cos x = 3\)

\(\Leftrightarrow {1 \over {\sqrt 5 }}\sin x - {2 \over {\sqrt 5 }}\cos x = {3 \over {\sqrt 5 }}\\ \Leftrightarrow \sin \left( {x - \alpha } \right) = {3 \over {\sqrt 5 }}\)

Trong đó α là số thỏa mãn \(\cos \alpha = {1 \over {\sqrt 5 }}\,\text{ và }\,\sin \alpha = {2 \over {\sqrt 5 }}.\)

Phương trình cuối cùng vô nghiệm do \({3 \over {\sqrt 5 }} > 1,\)  nên phương trình đã cho vô nghiệm.

b) \(5\sin2x + \sin x + \cos x + 6 = 0\)

Đặt \(t = \sin x + \cos x\), điều kiện \(\left| t \right| \le \sqrt 2\) ta được phương trình

\(5{t^2} + t + 1 = 0\) (vô nghiệm)

Vậy phương trình đã cho vô nghiệm.

Tìm các nghiệm của mỗi phương trình sau trong khoảng đã cho (khi cần tính gần đúng thì tính chính xác đến \({1 \over {10}}\) giây).

a) \(2{\sin ^2}x - 3\cos x = 2,0^\circ \le x \le 360^\circ\)

b) \(\tan x + 2\cot x = 3,180^\circ \le x \le 360^\circ\)

Phương pháp giải:

a) - Sử dụng công thức \(\sin^2a+\cos^2a=1\).

- Giải phương trình bậc hai ẩn cosx.

- Giải phương trình cơ bản của cos và tìm nghiệm thỏa \(0^0≤ x ≤ 360^0\).

b) - Tìm ĐKXĐ.

- Nhân hai vế phương trình cho tanx.

- Giải phương trình bậc hai ẩn tanx.

- Giải phương trình cơ bản của tan và tìm nghiệm thỏa 180^o ≤ x ≤ 360^o.

Hướng dẫn giải:

a) Ta có:

\(\eqalign{ & 2{\sin ^2}x - 3\cos x = 2 \Leftrightarrow 2{\cos ^2}x + 3\cos x = 0 \cr & \Leftrightarrow \cos x = 0\,\left( {\text{ loại }\,\cos x = - {3 \over 2}} \right) \cr & \Leftrightarrow x = 90^\circ + k180^\circ ,\,k \in \mathbb Z \cr}\)

Vậy với điều kiện \(0^0≤ x ≤ 360^0\), phương trình có hai nghiệm là \(x = 90^0\) và \(x = 270^0\).

b) \(\tan x + 2\cot x = 3,180^\circ \le x \le 360^\circ\)

ĐKXĐ: \(\sin x ≠ 0\) và \(\cos x ≠ 0\). Ta có:

\(\tan x + 2\cot x = 3 \\ \Leftrightarrow {\tan ^2}x - 3\tan x + 2 = 0 \\ \Leftrightarrow \left[ {\matrix{{\tan x = 1} \cr {\tan x = 2} \cr} } \right.\)

+ \(\tan x = 1 ⇔ x = 45^0 + k180^0\)

Có một nghiệm thỏa mãn 180^o ≤ x ≤ 360^o, ứng với k = 1 là x = 225^o

+ \(\tan x = 2 ⇔ x = α + k180^0\) với \(\tan α = 2\). Ta có thể chọn \(\alpha \approx {63^0}265,8\)

Vậy có một nghiệm (gần đúng) thỏa mãn \(180^0\le {\rm{ }}x{\rm{ }} \le {\rm{ }}360^0\) là: \(x = \alpha + {180^0} \approx {243^0}265,8\)

Kết luận: Với điều kiện 180^o ≤ x ≤ 360^o, phương trình có hai nghiệm x = 225^o và x ≈ 243^o265,8

Giải các phương trình sau:

a) \(3{\sin ^2}x - \sin 2x - {\cos ^2}x = 0\)

b) \(3{\sin ^2}2x - \sin 2x\cos 2x - 4{\cos ^2}2x = 2\)

c) \(2{\sin ^2}x + \left( {3 + \sqrt 3 } \right)\sin x\cos x + \left( {\sqrt 3 - 1} \right){\cos ^2}x = - 1\)

Phương pháp giải:

a) - Sử dụng công thức hạ bậc:

\({\sin ^2}a = \frac{{1 - \cos 2a}}{2},{\cos ^2}a = \frac{{1 + \cos 2a}}{2}\)

- Giải phương trình dạng asinx + bcosx = c:

+ Chia hai vế phương trình cho \(\sqrt{a^2+b^2}\)

+ Sử dụng công thức cos(a − b) = cosacosb + sinasinb để thu gọn phương trình.

b) c) - Chia hai vế phương trình cho cos²2x.

- Giải phương trình bậc hai ẩn tan x.

- Giải phương tình cơ bản của tan.

Hướng dẫn giải:

a) Ta có:

\(\eqalign{& 3{\sin ^2}x - \sin 2x - {\cos ^2}x = 0 \cr & \Leftrightarrow {{3\left( {1 - \cos 2x} \right)} \over 2} - \sin 2x - {{1 + \cos 2x} \over 2} = 0 \cr & \Leftrightarrow - 2\sin 2x - 4\cos 2x + 2 = 0 \cr & \Leftrightarrow \sin 2x + 2\cos 2x = 1 \cr & \Leftrightarrow {1 \over {\sqrt 5 }}\sin 2x + {2 \over {\sqrt 5 }}\cos 2x = {1 \over {\sqrt 5 }} \cr & \Leftrightarrow \cos \left( {2x - \alpha } \right) = \cos \left( {{\pi \over 2} - \alpha } \right) \cr & \text{ trong đó }\,\alpha \,\text{ là số thỏa mãn }\,\sin \alpha = {1 \over {\sqrt 5 }}\,\text{ và }\,\cos \alpha = {2 \over {\sqrt 5 }}.\text{ Ta có }\,: \cr & \cos \left( {2x - \alpha } \right) = \cos \left( {{\pi \over 2} - \alpha } \right) \cr & \Leftrightarrow 2x - \alpha = \pm \left( {{\pi \over 2} - \alpha } \right) + k2\pi \cr & \Leftrightarrow \left[ {\matrix{{x = {\pi \over 4} + k\pi } \cr {x = \alpha - {\pi \over 4} + k\pi } \cr} } \right.\left( {k \in \mathbb Z} \right) \cr}\)

b) \(3{\sin ^2}2x - \sin 2x\cos 2x - 4{\cos ^2}2x = 2\)

Những giá trị của x mà cos2x = 0 không là nghiệm phương trình. Chia hai vế phương trình cho cos²2x ta được:

\(\eqalign{& 3{\tan ^2}2x - \tan 2x - 4 = 2\left( {1 + {{\tan }^2}2x} \right) \cr & \Leftrightarrow {\tan ^2}2x - \tan 2x - 6 = 0 \Leftrightarrow \left[ {\matrix{{\tan 2x = - 2} \cr {\tan 2x = 3} \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{x = {\alpha \over 2} + k{\pi \over 2}} \cr {x = {\beta \over 2} + k{\pi \over 2}} \cr} } \right.\,\text{ trong đó }\,\tan 2\alpha = - 2\,\text{ và }\,\tan 2\beta = 3 \cr}\)

c) \(2{\sin ^2}x + \left( {3 + \sqrt 3 } \right)\sin x\cos x + \left( {\sqrt 3 - 1} \right){\cos ^2}x = - 1\)

Những giá trị của x mà cosx = 0 không là nghiệm phương trình. Chia hai vế phương trình cho cos²x ta được:

\(\eqalign{& 2{\tan ^2}x + \left( {3 + \sqrt 3 } \right)\tan x + \sqrt 3 - 1 = - \left( {1 + {{\tan }^2}x} \right) \cr & \Leftrightarrow 3{\tan ^2}x + \left( {3 + \sqrt 3 } \right)\tan x + \sqrt 3 = 0 \cr & \Leftrightarrow \left[ {\matrix{{\tan x = - 1} \cr {\tan x = - {{\sqrt 3 } \over 3}} \cr} } \right. \Leftrightarrow \left[ {\matrix{{x = - {\pi \over 4} + k\pi } \cr {x = - {\pi \over 6} + k\pi } \cr} } \right.\,\left( {k \in\mathbb Z} \right) \cr}\)

Giải các phương trình sau:

a) \(\sin x + \sin 2x + \sin 3x = \cos x + \cos 2x + \cos 3x\)

b) \(\sin x = \sqrt 2 \sin 5x - \cos x\)

c) \({1 \over {\sin 2x}} + {1 \over {\cos 2x}} = {2 \over {\sin 4x}}\)

d) \(\sin x + \cos x = {{\cos 2x} \over {1 - \sin 2x}}\)

Phương pháp giải:

a) Sử dụng công thức biến đổi tổng thành tích:

 \(\sin a + \sin b = 2\sin \frac{{a + b}}{2}\cos \frac{{a - b}}{2}\)

- Giải các phương trình lượng giác cơ bản.

b) - Biến đổi phương trình đã cho về dạng sin a = sin b

- Sử dụng công thức: \(\sin (a + b) = \sin a\cos b + \cos a\sin b\)

c) - Tìm ĐKXĐ.

- Nhân hai vế của phương trình cho sin4x.

- Sử dụng công thức: \(\sin (a + b) = \sin a\cos b + \cos a\sin b\).

d) - Tìm ĐKXĐ.

- Đặt nhân tử chung và giải các phương trình lượng giác cơ bản.

Hướng dẫn giải:

a) Ta có:

\(\eqalign{& \sin x + \sin 2x + \sin 3x = \cos x + \cos 2x + \cos 3x \cr & \Leftrightarrow \left( {\sin x + \sin 3x} \right) + \sin 2x = \left( {\cos x + \cos 3x} \right) + \cos 2x \cr & \Leftrightarrow 2\sin 2x\cos x + \sin 2x = 2\cos 2x\cos x + \cos 2x \cr & \Leftrightarrow \sin 2x\left( {2\cos x + 1} \right) - \cos 2x\left( {2\cos x + 1} \right) = 0 \cr & \Leftrightarrow \left( {2\cos x + 1} \right)\left( {\sin 2x - \cos 2x} \right) = 0 \cr & \Leftrightarrow \left[ {\matrix{{2\cos x + 1 = 0} \cr {\sin 2x - \cos 2x = 0} \cr} } \right. \Leftrightarrow \left[ {\matrix{{\cos x = - {1 \over 2}} \cr {\tan 2x = 1} \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{x = \pm {{2\pi } \over 3} + k2\pi } \cr {x = {\pi \over 8} + k{\pi \over 2}} \cr} } \right.,k \in\mathbb Z \cr}\)

b) Ta có:

\(\eqalign{& \sin x = \sqrt 2 \sin 5x - \cos x \cr & \Leftrightarrow {1 \over {\sqrt 2 }}\sin x + {1 \over {\sqrt 2 }}\cos x = \sin 5x \cr & \Leftrightarrow \sin \left( {x + {\pi \over 4}} \right) = \sin 5x \Leftrightarrow \left[ {\matrix{{5x = x + {\pi \over 4} + k2\pi } \cr {5x = {{3\pi } \over 4} - x + k2\pi } \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{x = {\pi \over {16}} + k{\pi \over 2}} \cr {x = {\pi \over 8} + k{\pi \over 3}} \cr} ,k \in\mathbb Z} \right. \cr}\)

c) \({1 \over {\sin 2x}} + {1 \over {\cos 2x}} = {2 \over {\sin 4x}}\)

ĐKXĐ: sin4x ≠ 0

Với điều kiện đó, ta có thể nhân hai vế của phương trình với sin4x:

\(\eqalign{& {1 \over {\sin 2x}} + {1 \over {\cos 2x}} = {2 \over {\sin 4x}} \cr & \Leftrightarrow {1 \over {\sin 2x}} + {1 \over {\cos 2x}} = {1 \over {\sin 2x\cos 2x}} \cr & \Leftrightarrow \sin 2x + \cos 2x = 1 \Leftrightarrow \sin \left( {2x + {\pi \over 4}} \right) = \sin {\pi \over 4} \cr & \Leftrightarrow \left[ {\matrix{{2x = k2\pi \ \text{(loại)} } \cr {2x = {\pi \over 2} + k2\pi \ \text{(loại)} } \cr} } \right. \cr}\)

Vậy phương trình đã cho vô nghiệm.

d) \(\sin x + \cos x = {{\cos 2x} \over {1 - \sin 2x}}\)

ĐKXĐ: \(\sin2x ≠ 1\). Với điều kiện đó ta có:

\(\eqalign{& \sin x + \cos x = {{\cos 2x} \over {1 - \sin 2x}} \cr & \Leftrightarrow \sin x + \cos x = {{{{\cos }^2}x - {{\sin }^2}x} \over {{{\left( {\cos x - \sin x} \right)}^2}}} \cr & \Leftrightarrow \left( {\sin x + \cos x} \right)\left( {1 - {1 \over {\cos x - \sin x}}} \right) = 0 \cr & +)\,\,\sin x + \cos x = 0 \Leftrightarrow x = - {\pi \over 4} + k\pi \cr & +)\,\,{1 \over {\cos x - \sin x}} = 1 \Leftrightarrow \cos x - \sin x = 1 \cr & \Leftrightarrow \cos \left( {x + {\pi \over 4}} \right) = {1 \over {\sqrt 2 }} \Leftrightarrow \left[ {\matrix{{x = k2\pi \,\left( \text{nhận} \right)} \cr {x = - {\pi \over 2} + k2\pi \,\left( \text{nhận}\right)} \cr} } \right. \cr}\)