Giải bài tập SGK Toán 11 Nâng cao Chương 4 Bài 2: Dãy số có giới hạn hữu hạn

Tìm các giới hạn sau:

a) \(\displaystyle \lim \left( {2 + {{{{\left( { - 1} \right)}^n}} \over {n + 2}}} \right)\)

b) \(\displaystyle \lim \left( {{{\sin 3n} \over {4n}} - 1} \right)\)

c) \(\displaystyle \lim {{n - 1} \over n}\)

d) \(\displaystyle \lim {{n + 2} \over {n + 1}}\)

Phương pháp giải:

a) b) Sử dụng phương pháp đánh giá và giới hạn kẹp:

Cho hai dãy số \(\left( {{u_n}} \right),\left( {{v_n}} \right)\). Nếu \(\left| {{u_n}} \right| \le {v_n}, \forall n\) mà \(\lim {v_n} = 0\) thì \(\lim {u_n} = 0\).

Và định nghĩa \(\lim \left( {{u_n} - L} \right) = 0\) thì \(\lim u_n=L\).

c) d) Chia cả tử và mẫu cho n và sử dụng giới hạn \(\lim \dfrac{1}{n} = 0\)

Hướng dẫn giải:

a) Đặt \(\displaystyle {u_n} = 2 + {{{{\left( { - 1} \right)}^n}} \over {n + 2}}\Rightarrow {u_n} - 2 = \dfrac{{{{\left( { - 1} \right)}^n}}}{{n + 2}}\)

Ta có:

\(\displaystyle \eqalign{ & \left| {{u_n} - 2} \right| = \left| {\frac{{{{\left( { - 1} \right)}^n}}}{{n + 2}}} \right|= {1 \over {n + 2}} < {1 \over n}\cr &\text{ Và }\,\lim {1 \over n} = 0 \cr & \Rightarrow \lim \left( {{u_n} - 2} \right) = 0 \Rightarrow \lim {u_n} = 2 \cr} \)

b) Đặt \(\displaystyle {u_n} = {{\sin 3n} \over {4n}} - 1 \Rightarrow {u_n} + 1 = \dfrac{{\sin 3n}}{{4n}}\)

Ta có:

\(\displaystyle \eqalign{ & \left| {{u_n} + 1} \right| = \left| {{{\sin 3n} \over {4n}}} \right| \le {1 \over {4n}}\cr &\text{ Và }\,\lim {1 \over {4n}} = 0 \cr & \Rightarrow \lim \left( {{u_n} + 1} \right) = 0 \Rightarrow \lim {u_n} = - 1 \cr} \)

c) \(\displaystyle \lim {{n - 1} \over n} = \lim \left( {1 - {1 \over n}} \right)\displaystyle = \lim 1 - \lim {1 \over n} = 1\)

d) \(\displaystyle \lim {{n + 2} \over {n + 1}} \)

\(= \lim {{n\left( {1 + {2 \over n}} \right)} \over {n\left( {1 + {1 \over n}} \right)}} \displaystyle \\= \lim {{1 + {2 \over n}} \over {1 + {1 \over n}}} \\= {{\lim 1 + \lim {2 \over n}} \over {\lim 1 + \lim {1 \over n}}} \displaystyle \\= {{1 + 0} \over {1 + 0}} = 1\)

Tìm \(\lim{\rm{ }}{u_n}\) với:

a) \({u_n} = {{{n^2} - 3n + 5} \over {2{n^2} - 1}}\)

b) \({u_n} = {{ - 2{n^2} + n + 2} \over {3{n^4} + 5}}\)

c) \({u_n} = {{\sqrt {2{n^2} - n} } \over {1 - 3{n^2}}}\)

d) \({u_n} = {{{4^n}} \over {{{2.3}^n} + {4^n}}}\)

Phương pháp giải:

- Chia cả tử và mẫu của biểu thức cần tính giới hạn cho lũy thừa bậc cao nhất của n và sử dụng giới hạn \(\lim \dfrac{1}{{{n^k}}} = 0\).

- Chia cả tử và mẫu \(u_n\) cho \(4^n\).

Hướng dẫn giải:

a) Ta có:

\(\eqalign{ & \lim{u_n} = \lim {{{n^2}\left( {1 - {3 \over n} + {5 \over {{n^2}}}} \right)} \over {{n^2}\left( {2 - {1 \over {{n^2}}}} \right)}} \cr &= \lim {{1 - {3 \over n} + {5 \over {{n^2}}}} \over {2 - {1 \over {{n^2}}}}} \cr & = {{\lim 1 - \lim {3 \over n} + \lim {5 \over {{n^2}}}} \over {\lim 2 - \lim {1 \over {{n^2}}}}}\cr & = {{1 - 0 + 0} \over {2 - 0}} = {1 \over 2} \cr} \)

b) Ta có:

\(\lim {u_n} = \lim {{{n^4}\left( {{{ - 2} \over {{n^2}}} + {1 \over {{n^3}}} + {{ 2} \over {{n^4}}}} \right)} \over {{n^4}\left( {3 + {5 \over {{n^4}}}} \right)}} \\\displaystyle = \lim {{{{ - 2} \over {{n^2}}} + {1 \over {{n^3}}} + {{ 2} \over {{n^4}}}} \over {3 + {5 \over {{n^4}}}}} \\={{0+0+0}\over {3+0}} \\= {0 \over 3} = 0\)

c) \(\lim {u_n} = \lim \dfrac{{\sqrt {2{n^2} - n} }}{{1 - 3{n^2}}}\)

\(\begin{array}{l} = \lim \dfrac{{\dfrac{{\sqrt {2{n^2} - n} }}{{{n^2}}}}}{{\dfrac{{1 - 3{n^2}}}{{{n^2}}}}} = \lim \dfrac{{\sqrt {\dfrac{{2{n^2} - n}}{{{n^4}}}} }}{{\dfrac{1}{{{n^2}}} - 3}}\\ = \lim \dfrac{{\sqrt {\dfrac{2}{{{n^2}}} - \dfrac{1}{{{n^3}}}} }}{{\dfrac{1}{{{n^2}}} - 3}} = \dfrac{{\sqrt {0 - 0} }}{{0 - 3}} = 0 \end{array}\)

d) Chia cả tử và mẫu \(u_n\) cho \(4^n\) ta được:

\(\begin{array}{l} \lim {u_n} = \lim \dfrac{{{4^n}}}{{{{2.3}^n} + {4^n}}}\\ = \lim \dfrac{{{4^n}}}{{{4^n}\left( {2.\dfrac{{{3^n}}}{{{4^n}}} + 1} \right)}}\\ = \lim \dfrac{1}{{2{{\left( {\dfrac{3}{4}} \right)}^n} + 1}} = \dfrac{1}{{2.0 + 1}} = 1 \end{array}\)

Cho dãy số (u_n) xác định bởi

\({u_1} = 10\,\text{ và }\,{u_{n + 1}} = {{{u_n}} \over 5} + 3\) với mọi n ≥ 1

a) Chứng minh rằng dãy số (v_n) xác định bởi \({v_n} = {u_n} - {{15} \over 4}\) là một cấp số nhân.

b)  Tìm \(\lim u_n\).

Phương pháp giải:

a) Dãy số (v_n) là cấp số nhân nếu \(v_{n+1}=q.v_n\) với q là số thực không đổi (công bội).

b) Tìm số hạng tổng quát \({v_n} = {v_1}{q^{n - 1}}\) suy ra giới hạn \(\lim v_n\).

Từ đó suy ra \(\lim u_n\).

Hướng dẫn giải:

a) Ta có: 

\(\displaystyle {v_{n + 1}} = {u_{n + 1}} - {{15} \over 4}\) \(\displaystyle = {{{u_n}} \over {5}} + 3 - {{15} \over 4} = {{{u_n}} \over 5} - {3 \over 4}\)

Thay \(\displaystyle {u_n} = {v_n} + {{15} \over 4}\) vào ta được:

\(\displaystyle {v_{n + 1}} = {1 \over 5}\left( {{v_n} + {{15} \over 4}} \right) - {3 \over 4} \) \(\displaystyle = \frac{1}{5}{v_n} + \frac{3}{4} - \frac{3}{4}= {1 \over 5}{v_n},\forall n\)

Vậy (v_n) là cấp số nhân lùi vô hạn với công bội \(\displaystyle q = {1 \over 5}\)

b) Ta có:

\(\eqalign{ & {v_1} = {u_1} - {{15} \over 4} = 10 - {{15} \over 4} = {{25} \over 4} \cr & {v_n} = {v_1}.{q^{n - 1}} = {{25} \over 4}.{\left( {{1 \over 5}} \right)^{n - 1}} \cr & \lim {\left( {\frac{1}{5}} \right)^{n - 1}} = 0\Rightarrow \lim {v_n} = 0\cr & \Rightarrow \lim \left( {{u_n} - \frac{{15}}{4}} \right) = 0\cr &\Rightarrow \lim {u_n} = {{15} \over 4} \cr} \)

Cho một tam giác đều ABC cạnh a. Tam giác A₁B₁C₁ có các đỉnh là trung điểm các cạnh của tam giác ABC, tam giác A₂B₂C₂ có các đỉnh là trung điểm các cạnh của tam giác A₁B₁C₁,…, tam giác A_n+1B_n+1C_n+1 có các đỉnh là trung điểm các cạnh của tam giác A_nB_nC_n, … . Gọi p₁, p₂, ..., p_n, … và S₁, S₂, …, S_n, … theo thứ tự là chu vi và diện tích của các tam giác

a) Tìm giới hạn của các dãy số (p_n) và (S_n).

b) Tìm các tổng \({p_1} + {p_2} + ... + {p_n} + ...\) và \({p_1} + {p_2} + ... + {p_n} + ...\)

Phương pháp giải:

a) - Chứng minh \({p_n} = \frac{{3a}}{{{2^n}}}\), \({S_n} = {{{a^2}\sqrt 3 } \over 4}.{\left( {{1 \over 4}} \right)^n}\) bằng phương pháp quy nạp.

- Sau đó tìm giới hạn của (p_n) và (S_n).

b) Sử dụng công thức tính tổng cấp số nhân lùi vô hạn \(S = \frac{{{u_1}}}{{1 - q}}\)

Hướng dẫn giải:

Ta có:

\({p_1} = {a \over 2} + {a \over 2} + {a \over 2} = {{3a} \over 2}; \\{p_2} = \frac{a}{4} + \frac{a}{4} + \frac{a}{4}= {{3a} \over 4} = {{3a} \over {{2^2}}} \\... \\ {p_n} = {{3a} \over {{2^n}}} (1)\)

Chứng minh bằng qui nạp:

+) Với n = 1 thì \({p_1} = \frac{{3a}}{2}\) (đúng).

+) Giả sử (1) đúng với n = k, tức là \({p_k} = {{3a} \over {{2^k}}}\).

Ta chứng minh (1) đúng với n = k + 1.

Tam giác \({A_{k + 1}}{B_{k + 1}}{C_{k + 1}}\) đồng dạng tam giác \(A_kB_kC_k\) theo tỉ số \(\frac{1}{2}\) 

Nên có chu vi \({p_{k + 1}} = \frac{1}{2}{p_k} = \frac{1}{2}.\frac{{3a}}{{{2^k}}} = \frac{{3a}}{{{2^{k + 1}}}}\)

Do đó ta có \({p_n} = \frac{{3a}}{{{2^n}}}\).

Vì \(\lim {1 \over {{2^n}}} = \lim {\left( {{1 \over 2}} \right)^n} = 0\text { nên }\lim {p_n} = 0\)

Diện tích tam giác ABC là \(S = {{{a^2}\sqrt 3 } \over 4}\). Diện tích tam giác A₁B₁C₁ là \({S_1} = {S \over 4}\)

Bằng phương pháp qui nạp, ta chứng minh được rằng diện tích tam giác \({A_n}{B_n}{C_n}\) là \({S_n} = {{{a^2}\sqrt 3 } \over 4}.{\left( {{1 \over 4}} \right)^n}\)

Vì \(\lim {\left( {{1 \over 4}} \right)^n} = 0\) nên \(\lim {S_n} = 0\).

b) Ta có (p_n) là cấp số nhân lùi vô hạn có công bội \(q = {1 \over 2},\) do đó:

\({p_1} + {p_2} + ... + {p_n} + ... = {{{p_1}} \over {1 - {1 \over 2}}}= 2{p_1}= 2.\frac{{3a}}{2} = 3a\)

(S_n) là cấp số nhân lùi vô hạn có công bội \(q' = {1 \over 4}\) do đó:

\({S_1} + {S_2} + ... + {S_n} + ... = {{{S_1}} \over {1 - {1 \over 4}}} = {4 \over 3}{S_1} = {S \over 3} = {{{a^2}\sqrt 3 } \over {12}}\)

Biểu diễn các số thập phân vô hạn tuần hoàn sau dưới dạng phân số:

a) 0,444…

b) 0,2121…

c) 0,32111…

Phương pháp giải:

Sử dụng công thức tính tổng cấp số nhân lùi vô hạn \(S = \frac{{{u_1}}}{{1 - q}}\)

Hướng dẫn giải:

a) Ta có:

\(\eqalign{ & 0,444... = 0,4 + 0,04 + 0,004 + ... \cr & = {4 \over {10}} + {4 \over {{{10}^2}}} + {4 \over {{{10}^3}}} + ... \cr & = 4\left( {{1 \over {10}} + {1 \over {{{10}^2}}} + ...} \right) \cr & = 4.{{{1 \over {10}}} \over {1 - {1 \over {10}}}} = {4 \over 9} \cr} \)

b) Ta có:

\(\eqalign{ & 0,2121... = 0,21 + 0,0021 + ... \cr & = {{21} \over {{{10}^2}}} + {{21} \over {{{10}^4}}} + ... \cr &= 21\left( {{1 \over {{{10}^2}}} + {1 \over {{{10}^4}}} + ...} \right) \cr & = 21.{{{1 \over {{{10}^2}}}} \over {1 - {1 \over {{{10}^2}}}}} = {{21} \over {99}} = {7 \over {33}} \cr} .\)

c) Ta có:

\(\eqalign{ & 0,32111...\cr & = {{32} \over {100}} + {1 \over {1000}} + {1 \over {10000}}+ ... \cr & = \frac{{32}}{{100}} + \frac{1}{{1000}}\left( {1 + \frac{1}{{10}} + \frac{1}{{{{10}^2}}} + ...} \right)\cr &= {{32} \over {100}} + {1 \over {1000}}.{1 \over {1 - {1 \over {10}}}}\cr & = {{32} \over {100}} + {1 \over {900}} = {{289} \over {900}} \cr} \)

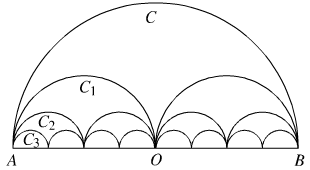
Gọi C là nửa đường tròn đường kính AB = 2R, C₁ là đường gồm hai nửa đường tròn đường kính \({{AB} \over 2}\), C₂ là đường gồm bốn nửa đường tròn đường kính \({{AB} \over 4},...\) C_n là đường gồm \(2^n\) nửa đường tròn đường kính \({{AB} \over {{2^n}}},...\). Gọi p_n là độ dài của C_n, S_n là diện tích hình phẳng giới hạn bởi C_n và đoạn thẳng AB.

a) Tính p_n và S_n.

b) Tìm giới hạn của các dãy số (p_n) và (S­_n).

Phương pháp giải:

Sử dụng công thức tính chu vi và diện tích hình tròn:

+) Chu vi \(2\pi R\).

+) Diện tích \(\pi {R^2}.\)

Hướng dẫn giải:

a) Ta có: 

\({p_n} = {2^n}.{R \over {{2^n}}}.\pi = \pi R\) với mọi n

\({S_n} = {2^n}.{\left( {{R \over {{2^n}}}} \right)^2}.{\pi \over 2} = {{\pi {R^2}} \over 2}.{1 \over {{2^n}}}\)

b) Ta có:

\(\begin{array}{l} \lim {p_n} = \lim \pi R = \pi R\\ \lim {S_n} = \lim \dfrac{{\pi {R^2}}}{{{2^{n + 1}}}} = 0 \end{array}\)