Giải bài tập SGK Toán 11 Nâng cao Ôn tập chương 1: Hàm số lượng giác và phương trình lượng giác
Nội dung giải bài tập trang 47, 78, 79 SGK Toán 11 Nâng cao bài Ôn tập chương 1 bên dưới đây sẽ giúp các em học thật tốt môn Toán. Qua tài liệu này các em sẽ nắm được phương pháp giải cụ thể của từng bài từ đó đưa ra lời giải phù hợp với đề ra. Mời các em cùng tham khảo.
Mục lục nội dung
1. Giải bài 43 trang 47 SGK Đại số & Giải tích 11 Nâng cao
2. Giải bài 44 trang 47 SGK Đại số & Giải tích 11 Nâng cao
3. Giải bài 45 trang 47 SGK Đại số & Giải tích 11 Nâng cao
4. Giải bài 46 trang 48 SGK Đại số & Giải tích 11 Nâng cao
5. Giải bài 47 trang 48 SGK Đại số & Giải tích 11 Nâng cao
6. Giải bài 48 trang 48 SGK Đại số & Giải tích 11 Nâng cao
7. Giải bài 49 trang 48 SGK Đại số & Giải tích 11 Nâng cao
8. Giải bài 50 trang 48 SGK Đại số & Giải tích 11 Nâng cao
9. Giải bài 51 trang 48 SGK Đại số & Giải tích 11 Nâng cao
10. Giải bài 52 trang 48 SGK Đại số & Giải tích 11 Nâng cao
11. Giải bài 53 trang 49 SGK Đại số & Giải tích 11 Nâng cao
12. Giải bài 54 trang 49 SGK Đại số & Giải tích 11 Nâng cao
13. Giải bài 55 trang 49 SGK Đại số & Giải tích 11 Nâng cao
14. Giải bài 56 trang 49 SGK Đại số & Giải tích 11 Nâng cao
15. Giải bài 57 trang 49 SGK Đại số & Giải tích 11 Nâng cao
16. Giải bài 58 trang 49 SGK Đại số & Giải tích 11 Nâng cao
17. Giải bài 59 trang 49 SGK Đại số & Giải tích 11 Nâng cao
18. Giải bài 60 trang 49 SGK Đại số & Giải tích 11 Nâng cao
19. Giải bài 61 trang 49 SGK Đại số & Giải tích 11 Nâng cao

1. Giải bài 43 trang 47 SGK Đại số & Giải tích 11 Nâng cao
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai ?
a) Các hàm số y = sin x, y = cos x có cùng tập xác định.
b) Các hàm số y = tan x, y = cot x có cùng tập xác định.
c) Các hàm số y = sin x, y = tan x là những hàm số lẻ.
d) Các hàm số y = cos x, y = cot x là những hàm số chẵn.
e) Các hàm số y = sin x, y = cos x cùng nghịch biến trên khoảng \( \left( {{\pi \over 2};{{3\pi } \over 2}} \right)\).
f) Hàm số y = cos x nghịch biến trên khoảng (-2π; -π).
g) Trên mỗi khoảng mà hàm số y = tan x đồng biến thì hàm số y = cot x nghịch biến.
Phương pháp giải:
a) b) Tìm TXĐ của hai hàm số và kết luận.
c) d) Xét tính chẵn lẻ của từng hàm số và kết luận.
e) f) g) Xét tính đơn điệu của các hàm số và kết luận.
Hướng dẫn giải:
a) Đúng vì hàm số y = sin x, y = cos x có cùng tập xác định D = R.
b) Sai vì y = tan x xác định \(∀x \ne {\pi \over 2} + k\pi \) còn y = cot x xác định \(∀x ≠ kπ\).
c) Đúng.
d) Sai vì y = cot x là hàm số lẻ.
e) Sai vì y = cos x không nghịch biến trên khoảng \( \left( {{\pi \over 2};{{3\pi } \over 2}} \right)\).
f) Đúng.
g) Sai vì trên khoảng \(\left( { - {\pi \over 2};{\pi \over 2}} \right)\) hàm số y = tan x đồng biến nhưng hàm số y = cot x không nghịch biến.
2. Giải bài 44 trang 47 SGK Đại số & Giải tích 11 Nâng cao
Xét hàm số \(y = f(x) = \sinπx.\)
a) Chứng minh rằng với mỗi số nguyên chẵn m ta có f (x + m) = f(x) với mọi x.
b) Lập bảng biến thiên của hàm số trên đoạn [-1 ; 1].
c) Vẽ đồ thị của hàm số.
Phương pháp giải:
a) Tính f (x + m) và so sánh với f(x).
b) Vẽ bảng biến thiên của hàm số trên đoạn [-1 ; 1].
c) Vẽ đồ thị của hàm số đó.
Hướng dẫn giải:
Đặt \(m = 2k, k \in\mathbb Z\). Ta có:
\( f(x + m) \\= \sinπ(x + m) \\ = \sin(πx + 2kπ) \\ = \sinπx = f(x)\)
b) Bảng biến thiên

c) Đồ thị:
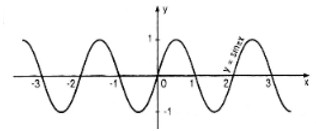
3. Giải bài 45 trang 47 SGK Đại số & Giải tích 11 Nâng cao
Đưa các biểu thức sau về dạng \(C\sin(x + α)\)
a) \( \sin x + \tan {\pi \over 7}\cos x\)
b) \( \tan {\pi \over 7}\sin x + \cos x\)
Phương pháp giải:
a) Sử dụng các công thức sau để biến đổi:
\(\tan a = \frac{{\sin a}}{{\cos a}}\)
\(\sin (a + b) = \sin a\cos b + \cos a\sin b\)
b) Sử dụng các công thức sau để biến đổi:
\(\tan a = \frac{{\sin a}}{{\cos a}}\)
\(\cos (a + b) = \cos a\cos b - \sin a\sin b\)
Hướng dẫn giải:
a) Ta có:
\( \begin{array}{l} \sin x + \tan \dfrac{\pi }{7}\cos x\\ = \sin x + \dfrac{{\sin \dfrac{\pi }{7}}}{{\cos \dfrac{\pi }{7}}}.\cos x\\ = \sin x + \dfrac{{\sin \dfrac{\pi }{7}\cos x}}{{\cos \dfrac{\pi }{7}}}\\ = \dfrac{{\sin x\cos \dfrac{\pi }{7} + \sin \dfrac{\pi }{7}\cos x}}{{\cos \dfrac{\pi }{7}}}\\ = \dfrac{{\sin \left( {x + \dfrac{\pi }{7}} \right)}}{{\cos \dfrac{\pi }{7}}} \end{array} \)
\(= \dfrac{1}{{\cos \dfrac{\pi }{7}}}\sin \left( {x + \dfrac{\pi }{7}} \right)\)
b)
\( \begin{array}{l} \tan \dfrac{\pi }{7}\sin x + \cos x\\ = \dfrac{{\sin \dfrac{\pi }{7}}}{{\cos \dfrac{\pi }{7}}}.\sin x + \cos x\\ = \dfrac{{\sin \dfrac{\pi }{7}\sin x}}{{\cos \dfrac{\pi }{7}}} + \cos x\\ = \dfrac{{\sin \dfrac{\pi }{7}\sin x + \cos x\cos \dfrac{\pi }{7}}}{{\cos \dfrac{\pi }{7}}}\\ = \dfrac{{\cos \left( {x - \dfrac{\pi }{7}} \right)}}{{\cos \dfrac{\pi }{7}}} = \dfrac{{\cos \left( {\dfrac{\pi }{7} - x} \right)}}{{\cos \dfrac{\pi }{7}}}\\ = \dfrac{{\sin \left( {\dfrac{\pi }{2} - \dfrac{\pi }{7} + x} \right)}}{{\cos \dfrac{\pi }{7}}}\\ = \dfrac{{\sin \left( {\dfrac{{5\pi }}{{14}} + x} \right)}}{{\cos \dfrac{\pi }{7}}}\\ = \dfrac{1}{{\cos \dfrac{\pi }{7}}}\sin \left( {x + \dfrac{{5\pi }}{{14}}} \right) \end{array}\)
4. Giải bài 46 trang 48 SGK Đại số & Giải tích 11 Nâng cao
Giải các phương trình sau:
a) \(\sin \left( {x - {{2\pi } \over 3}} \right) = \cos 2x\)
b) \( \tan \left( {2x + 45^\circ } \right)\tan \left( {180^\circ - {x \over 2}} \right) = 1\)
c) \( \cos 2x - {\sin ^2}x = 0\)
d) \( 5\tan x - 2\cot x = 3\)
Phương pháp giải:
a) - Sử dụng công thức \(\cos x = \sin \left( {\frac{\pi }{2} - x} \right)\)
- Giải phương trình cơ bản của sin.
b) Sử dụng công thức:
\( \tan \left( {180^\circ - x} \right) = \tan \left( { - x} \right)\)
tan x.cot x = 1
c) Sử dụng công thức hạ bậc \({\sin ^2}a = \frac{{1 - \cos 2a}}{2}\)
d) Sử dụng công thức tan x.cot x = 1 để biến đổi phương trình thành phương trình bậc 2 theo tan x.
Hướng dẫn giải:
a) Ta có:
\( \eqalign{& \sin \left( {x - {{2\pi } \over 3}} \right) = \cos 2x \cr & \Leftrightarrow \sin \left( {x - {{2\pi } \over 3}} \right) = \sin \left( {{\pi \over 2} - 2x} \right) \cr & \Leftrightarrow \left[ {\matrix{{x - {{2\pi } \over 3} = {\pi \over 2} - 2x + k2\pi } \cr {x - {{2\pi } \over 3} = \pi - {\pi \over 2} + 2x + k2\pi } \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{x = {{7\pi } \over {18}} + k{{2\pi } \over 3}} \cr {x = - {{7\pi } \over 6} - k2\pi } \cr} } \right. \cr}\)
b) Với ĐKXĐ của phương trình ta có:
\( \tan \left( {2x + {{45}^0}} \right) = \cot \left( {{{90}^0} - 2x - {{45}^0}} \right) = \cot \left( {{{45}^0} - 2x} \right)\)
\( \tan \left( {180^\circ - {x \over 2}} \right) = \tan \left( { - {x \over 2}} \right)\)
Nên:
\( \eqalign{ & \tan \left( {2x + 45^\circ } \right)\tan \left( {180^\circ - {x \over 2}} \right) = 1 \cr & \Leftrightarrow \cot \left( {45^\circ - 2x} \right)\tan \left( { - {x \over 2}} \right) = 1 \cr & \Leftrightarrow \tan \left( { - \frac{x}{2}} \right) = \frac{1}{{\cot \left( {{{45}^0} - 2x} \right)}}\cr&\Leftrightarrow \tan \left( { - {x \over 2}} \right) = \tan \left( {45^\circ - 2x} \right) \cr & \Leftrightarrow - {x \over 2} = 45^\circ - 2x + k180^\circ \cr & \Leftrightarrow x = 30^\circ + k120^\circ,k \in\mathbb Z \cr}\)
c) Ta có:
\( \eqalign{ & \cos 2x - {\sin ^2}x = 0 \cr & \Leftrightarrow \cos 2x - {{1 - \cos 2x} \over 2} = 0 \cr & \Leftrightarrow 3\cos 2x - 1 = 0 \Leftrightarrow \cos 2x = {1 \over 3} \cr & \Leftrightarrow \cos 2x = \cos \alpha \,\left( {\text{ với }\,\cos \alpha = {1 \over 3}} \right) \cr & \Leftrightarrow x = \pm {\alpha \over 2} + k\pi \,\,(k\in\mathbb Z)\cr}\)
d)
\( \eqalign{& 5\tan x - 2\cot x = 3 \cr & \Leftrightarrow 5\tan x - {2 \over {\tan x}} = 3 \cr & \Leftrightarrow 5{\tan ^2}x - 3\tan x - 2 = 0 \cr & \Leftrightarrow \left[ {\matrix{{\tan x = 1} \cr {\tan x = - {2 \over 5}} \cr} } \right. \Leftrightarrow \left[ {\matrix{{x = {\pi \over 4} + k\pi } \cr {x = \alpha + k\pi } \cr}k\in\mathbb Z } \right. \cr & \text{Trong đó}\,\tan \alpha = - {2 \over 5} \cr}\)
5. Giải bài 47 trang 48 SGK Đại số & Giải tích 11 Nâng cao
Giải các phương trình sau:
a) \( \sin 2x + {\sin ^2}x = {1 \over 2}\)
b) \( 2{\sin ^2}x + 3\sin x\cos x + {\cos ^2}x = 0\)
c) \( {\sin ^2}{x \over 2} + \sin x - 2{\cos ^2}{x \over 2} = {1 \over 2}\)
Phương pháp giải:
a) Sử dụng công thức hạ bậc: \({\sin ^2}a = \frac{{1 - \cos 2a}}{2}\)
b) - Chia hai vế phương trình cho \({\cos ^2}x\) .
- Giải phương trình bậc hai ẩn tan x.
- Giải phương trình cơ bản của tan.
c)- Chia hai vế phương trình cho \({\cos ^2}{x \over 2}\).
- Giải phương trình bậc hai ẩn \(\tan \dfrac x2\).
- Giải phương trình cơ bản của tan.
Hướng dẫn giải:
a) Ta có:
\( \eqalign{ & \sin 2x + {\sin ^2}x = {1 \over 2} \cr & \Leftrightarrow \sin 2x + {1 \over 2}\left( {1 - \cos 2x} \right) = {1 \over 2} \cr & \Leftrightarrow \sin 2x - {1 \over 2}\cos 2x = 0 \cr & \Leftrightarrow \tan 2x = {1 \over 2} \cr & \Leftrightarrow 2x = \alpha + k\pi \,\text{ với }\,\tan \alpha = {1 \over 2} \cr & \Leftrightarrow x = {\alpha \over 2} + k{\pi \over 2},\,k \in\mathbb Z \cr}\)
b) \(x = {\pi \over 2} + k\pi \) không là nghiệm phương trình.
Chia hai vế phương trình cho \({\cos ^2}x\) ta được:
\( \eqalign{& 2{\tan ^2}x + 3\tan x + 1 = 0 \Leftrightarrow \left[ {\matrix{{\tan x = - 1} \cr {\tan x = - {1 \over 2}} \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{x = - {\pi \over 4} + k\pi } \cr {x = \alpha + k\pi } \cr} } \right.\,\left( {k \in\mathbb Z} \right) \cr & \left( {\text{ với }\,\tan \alpha = - {1 \over 2}} \right) \cr}\)
c) Ta có:
\( \eqalign{ & {\sin ^2}{x \over 2} + \sin x - 2{\cos ^2}{x \over 2} = {1 \over 2} \cr & \Leftrightarrow {\sin ^2}{x \over 2} + 2\sin {x \over 2}\cos {x \over 2} - 2{\cos ^2}{x \over 2} = {1 \over 2} \cr} \)
Với x mà \(\cos {x \over 2} = 0\) không là nghiệm phương trình.
Chia hai vế phương trình cho \({\cos ^2}{x \over 2}\) ta được:
\( \eqalign{& {\tan ^2}{x \over 2} + 2\tan {x \over 2} - 2 = {1 \over 2}\left( {1 + {{\tan }^2}{x \over 2}} \right) \cr & \Leftrightarrow {\tan ^2}{x \over 2} + 4\tan {x \over 2} - 5 = 0 \cr & \Leftrightarrow \left[ {\matrix{{\tan {x \over 2} = 1} \cr {\tan {x \over 2} = - 5} \cr} } \right. \Leftrightarrow \left[ {\matrix{{{x \over 2} = {\pi \over 4} + k\pi } \cr {{x \over 2} = \alpha + k\pi } \cr} } \right.\,\left( {\text{ với }\,\tan \alpha = - 5} \right) \cr & \Leftrightarrow \left[ {\matrix{{x = {\pi \over 2} + k2\pi } \cr {x = 2\alpha + k2\pi } \cr} } \right.\,\left( {k \in\mathbb Z} \right) \cr}\)
6. Giải bài 48 trang 48 SGK Đại số & Giải tích 11 Nâng cao
a) Chứng minh rằng \(\sin {\pi \over {12}} = {{\sqrt 3 - 1} \over {2\sqrt 2 }}\)
b) Giải các phương trình \(2\sin x – 2\cos x =1 - \sqrt 3 \) bằng cách biến đổi vế trái về dạng \(C\sin(x + α).\)
c) Giải phương trình \(2\sin x – 2\cos x =1 - \sqrt 3 \) bằng cách bình phương hai vế.
Phương pháp giải:
a) - Thay \(\frac{\pi }{{12}} = \frac{\pi }{3} - \frac{\pi }{4}\)
- Sử dụng công thức \(\sin (a + b) = \sin a\cos b + \cos a\sin b\) để chứng minh.
b) - Chia hai vế của phương trình cho \(2\sqrt2\).
- Sử dụng công thức \(\sin (a - b) = \sin a\cos b - \cos a\sin b\) để biến đổi về dạng \(C\sin(x + α).\)
- Giải phương trình cơ bản của sin và kết luận.
c) - Bình phương hai vế.
- Sử dụng công thức \(\sin^2x+\cos^2x=1\) để thu gọn phương trình.
- Giải phương trình cơ bản của sin và tìm nghiệm.
Hướng dẫn giải:
a) Ta có:
\( \eqalign{ & \sin {\pi \over {12}} = \sin \left( {{\pi \over 3} - {\pi \over 4}} \right) \cr & = \sin {\pi \over 3}\cos {\pi \over 4} - \sin {\pi \over 4}\cos {\pi \over 3} \cr & = {{\sqrt 3 } \over 2}.{{\sqrt 2 } \over 2} - {{\sqrt 2 } \over 2}.{1 \over 2} \cr & = {{\sqrt 6 - \sqrt 2 } \over 4} = {{\sqrt 2 \left( {\sqrt 3 - 1} \right)} \over 4} \cr & = {{\sqrt 3 - 1} \over {2\sqrt 2 }} \cr}\)
b) Ta có:
\( \eqalign{& 2\sin x - 2\cos x = 1 - \sqrt 3 \cr & \Leftrightarrow {1 \over {\sqrt 2 }}\sin x - {1 \over {\sqrt 2 }}\cos x = {{1 - \sqrt 3 } \over {2\sqrt 2 }} \cr & \Leftrightarrow \sin x.\cos {\pi \over 4} - \sin {\pi \over 4}\cos x = - \sin {\pi \over {12}} \cr & \Leftrightarrow \sin \left( {x - {\pi \over 4}} \right) = \sin \left( { - {\pi \over {12}}} \right) \cr & \Leftrightarrow \left[ {\matrix{{x - {\pi \over 4} = - {\pi \over {12}} + k2\pi } \cr {x - {\pi \over 4} = \pi + {\pi \over {12}} + k2\pi } \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{x = {\pi \over 6} + k2\pi } \cr {x = {{4\pi } \over 3} + k2\pi } \cr} } \right.\left( {k \in\mathbb Z} \right) \cr}\)
c)Ta có: \( 1 - \sqrt 3 < 0\), ta đặt điều kiện \(\sin x – \cos x < 0\) rồi bình phương hai vế của phương trình thì được:
\( \eqalign{& 4\left( {1 - \sin 2x} \right) = 4 - 2\sqrt 3 \cr & \Leftrightarrow \sin 2x = {{\sqrt 3 } \over 2} \Leftrightarrow \left[ {\matrix{{x = {\pi \over 6} + k\pi } \cr {x = {\pi \over 3} + k\pi } \cr}\,\,(k\in\mathbb Z) } \right. \cr} \)
Thử vào điều kiện \(\sin x – \cos x < 0\), ta thấy:
+ Họ nghiệm \(x = {\pi \over 6} + k\pi \) thỏa mãn điều kiện sin x – cos x < 0 khi và chỉ khi k chẵn, tức là \(x = {\pi \over 6} + 2m\pi \) với \(m \in\mathbb Z.\)
+ Họ nghiệm \(x = {\pi \over 3} + k\pi \) thỏa mãn điều kiện sin x – cos x < 0 khi và chỉ khi k lẻ, tức là \(x = {\pi \over 3} + \left( {2m + 1} \right)\pi = {{4\pi } \over 3} + 2m\pi \) với \(m \in\mathbb Z.\)
Ta có kết quả như đã nêu ở câu b.
7. Giải bài 49 trang 48 SGK Đại số & Giải tích 11 Nâng cao
Giải phương trình:
\( {{1 + \cos 2x} \over {\cos x}} = {{\sin 2x} \over {1 - \cos 2x}}\)
Phương pháp giải:
- Tìm ĐKXĐ.
- Biến đổi phương trình bằng cách sử dụng các công thức sau:
\(\cos 2x = 2{\cos ^2}x - 1\)
\(\sin 2x = 2\sin x\cos x\)
- Giải phương trình cơ bản của sin và kết luận.
Hướng dẫn giải:
ĐKXĐ: \( \cos x \ne 0\,\text{ và }\,\cos 2x \ne 1\).
Với điều kiện đó, ta có:
\( \eqalign{& {{1 + \cos 2x} \over {\cos x}} = {{\sin 2x} \over {1 - \cos 2x}} \cr & \Leftrightarrow {{2{{\cos }^2}x} \over {\cos x}} = {{2\sin x\cos x} \over {2{{\sin }^2}x}} \cr & \Leftrightarrow 1 - {1 \over {2\sin x}} = 0 \cr & \Leftrightarrow \sin x = {1 \over 2} \Leftrightarrow \left[ {\matrix{{x = {\pi \over 6} + k2\pi \,\left( \text{nhận} \right)} \cr {x = {{5\pi } \over 6} + k2\pi \,\left( \text{nhận} \right)} \cr} } \right. \cr}\)
8. Giải bài 50 trang 48 SGK Đại số & Giải tích 11 Nâng cao
Cho phương trình \( {{{{\sin }^3}x + {{\cos }^3}x} \over {2\cos x - \sin x}} = \cos 2x.\)
a) Chứng minh rằng \(x = {\pi \over 2} + k\pi \) nghiệm đúng phương trình.
b) Giải phương trình bằng cách đặt tan x = t (khi \(x \ne {\pi \over 2} + k\pi \))
Phương pháp giải:
a) Thay \(x = {\pi \over 2} + k\pi \) vào phương trình.
b) - Đặt tan x = t, giải phương trình ẩn t.
- Giải phương trình cơ bản ủa tan để tìm nghiệm x.
Hướng dẫn giải:
a) Ta có: \(\sin \left( {\frac{\pi }{2} + k\pi } \right) = {\left( { - 1} \right)^k}\)
(nghĩa là bằng 1 nếu k chẵn, bằng -1 nếu k lẻ)
Thay \(x = {\pi \over 2} + k\pi \) vào phương trình ta được:
\( \begin{array}{l} \frac{{{{\sin }^3}\left( {\frac{\pi }{2} + k\pi } \right) + {{\cos }^3}\left( {\frac{\pi }{2} + k\pi } \right)}}{{2\cos \left( {\frac{\pi }{2} + k\pi } \right) - \sin \left( {\frac{\pi }{2} + k\pi } \right)}} = \cos \left[ {2\left( {\frac{\pi }{2} + k\pi } \right)} \right]\\ \Leftrightarrow \frac{{{{\left( { - 1} \right)}^{3k}} + 0}}{{2.0 - {{\left( { - 1} \right)}^k}}} = \cos \left( {\pi + k2\pi } \right)\\ \Leftrightarrow \frac{{{{\left( { - 1} \right)}^{3k}}}}{{ - {{\left( { - 1} \right)}^k}}} = \cos \pi \\ \Leftrightarrow - {\left( { - 1} \right)^{2k}} = - 1\\ \Leftrightarrow - 1 = - 1 \end{array}\)
Vậy \(x = {\pi \over 2} + k\pi \) là nghiệm phương trình
b) Ta có:
+ \(x = {\pi \over 2} + k\pi \) là nghiệm phương trình.
+ Với \(x \ne {\pi \over 2} + k\pi \) chia tử và mẫu của vế trái cho \({\cos ^3}x\) ta được:
\( {{{{\tan }^3}x + 1} \over {2\left( {1 + {{\tan }^2}x} \right) - \tan x\left( {1 + {{\tan }^2}x} \right)}} = {{1 - {{\tan }^2}x} \over {1 + {{\tan }^2}x}}\)
Đặt t = tan x ta được:
\( \eqalign{& {{{t^3} + 1} \over {\left( {2 - t} \right)\left( {1 + {t^2}} \right)}} = {{1 - {t^2}} \over {1 + {t^2}}} \cr & \Leftrightarrow {t^3} + 1 = \left( {{t^2} - 1} \right)\left( {t - 2} \right) \cr & \Leftrightarrow {t^3} + 1 = {t^3} - 2{t^2} - t + 2 \cr & \Leftrightarrow 2{t^2} + t - 1 = 0 \Leftrightarrow \left[ {\matrix{ {t = - 1} \cr {t = {1 \over 2}} \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{\tan x = - 1} \cr {\tan x = {1 \over 2}} \cr} } \right. \Leftrightarrow \left[ {\matrix{{x = - {\pi \over 4} + k\pi } \cr {x = \alpha + k\pi } \cr} } \right. \cr & \text{ với }\,\tan \alpha = {1 \over 2} \cr}\)
Vậy phương trình đã cho có nghiệm:
\(x = {\pi \over 2} + k\pi,x = - {\pi \over 4} + k\pi, x = \alpha + k\pi \,\left( {k \in\mathbb Z} \right)\)
9. Giải bài 51 trang 48 SGK Đại số & Giải tích 11 Nâng cao
Giá trị lớn nhất của các biểu thức \({\sin ^4}x + {\cos ^4}x\) là:
A. 0
B. 1
C. 2
D. \( {1 \over 2}\)
Phương pháp giải:
Sử dụng hằng đẳng thức:
\(\begin{array}{l} {(a + b)^2} = {a^2} + 2ab + {b^2}\\ \Rightarrow {a^2} + {b^2} = {(a + b)^2} - 2ab \end{array}\)
Hướng dẫn giải:
Ta có:
\( {\sin ^4}x + {\cos ^4}x \\ = \left( {{{\sin }^2}x + {{\cos }^2}x} \right)^2 - 2{\sin ^2}x{\cos ^2}x \\ = 1 - 2{\sin ^2}x{\cos ^2}x \le 1\)
Chọn B.
10. Giải bài 52 trang 48 SGK Đại số & Giải tích 11 Nâng cao
Giá trị bé nhất của biểu thức \(\sin x + \sin \left( {x + {{2\pi } \over 3}} \right)\) là
A. -2
B. \( {{\sqrt 3 } \over 2}\)
C. -1
D. 0
Phương pháp giải:
Sử dụng công thức biến đổi tổng thành tích:
\(\sin a + \sin b = 2\sin \frac{{a + b}}{2}\cos \frac{{a - b}}{2}\)
Hướng dẫn giải:
Ta có: \( \sin x + \sin \left( {x + {{2\pi } \over 3}} \right)\)
\( =2\sin \left( {x + {\pi \over 3}} \right)\cos {\pi \over 3} \\ = \sin \left( {x + {\pi \over 3}} \right) \ge - 1\)
Chọn C.
11. Giải bài 53 trang 49 SGK Đại số & Giải tích 11 Nâng cao
Tập giá trị của hàm số y = 2sin2x + 3 là:
A. [0 ; 1]
B. [2 ; 3]
C. [-2 ; 3]
D. [1 ; 5]
Phương pháp giải:
Sử dụng tính chất -1 ≤ sinx ≤ 1.
Hướng dẫn giải:
Ta có: \(-1 ≤ \sin 2x ≤ 1 \Rightarrow - 2 \le 2\sin 2x \le 2\)
\( \Rightarrow 1 \le 2\sin 2x + 3 \le 5\)
⇒ 1 ≤ y ≤ 5
Chọn D.
12. Giải bài 54 trang 49 SGK Đại số & Giải tích 11 Nâng cao
Tập giá trị của hàm số y = 1 – 2|sin3x| là:
A. [-1 ; 1]
B. [0 ; 1]
C. [-1 ; 0]
D. [-1 ; 3]
Phương pháp giải:
Sử dụng tính chất 0 ≤ |sinx| ≤ 1.
Hướng dẫn giải:
Vì 0 ≤ |sin3x| ≤ 1 nên -1 ≤ y ≤ 1
Chọn A.
13. Giải bài 55 trang 49 SGK Đại số & Giải tích 11 Nâng cao
Giá trị lớn nhất của biểu thức \(y = {\cos ^2}x - \sin x\) là:
A. 2
B. 0
C. \( {5 \over 4}\)
D. 1
Phương pháp giải:
Sử dụng công thức \(\sin^2x+\cos^2x=1\) để rút gọn y.
⇒ GTLN của hàm số.
Hướng dẫn giải:
Ta có:
\( \eqalign{ & y = 1 - {\sin ^2}x - \sin x \cr&= 1 - \left( {{{\sin }^2}x + \sin x} \right) \cr & = {5 \over 4} - \left( {{{\sin }^2}x + \sin x + {1 \over 4}} \right) \cr&= {5 \over 4} - {\left( {\sin x + {1 \over 2}} \right)^2} \le {5 \over 4} \cr}\)
Chọn C.
14. Giải bài 56 trang 49 SGK Đại số & Giải tích 11 Nâng cao
Tập giá trị của hàm số \(y = 4\cos2x – 3\sin2x + 6\) là:
A. [3 ; 10]
B. [6 ; 10]
C. [-1 ; 13]
D. [1 ; 11]
Phương pháp giải:
- Đặt 5 làm nhân tử chung.
- Sử dụng công thức cộng: \(\cos (a + b) = \cos a \cos b - \sin a \sin b\) để rút dọn hàm số.
- Tìm GTLN, GTNN của hàm số.
Hướng dẫn giải:
Ta có:
\( \eqalign{& 4\cos 2x - 3\sin 2x\cr& = 5\left( {{4 \over 5}\cos 2x - {3 \over 5}\sin 2x} \right) \cr & = 5\left( {\cos 2x\cos \alpha - \sin 2x\sin \alpha } \right)\cr&\text{với}\,\left\{ {\matrix{{\cos \alpha = {4 \over 5}} \cr {\sin \alpha = {3 \over 5}} \cr} } \right. \cr & = 5\cos \left( {2x + \alpha } \right) \cr&\Rightarrow y = 6 + 5\cos \left( {2x + \alpha } \right)\cr& \Rightarrow 1 \le y \le 11 \cr}\)
Chọn D.
15. Giải bài 57 trang 49 SGK Đại số & Giải tích 11 Nâng cao
Khi x thay đổi trong khoảng \(\left( {{{5\pi } \over 4};{{7\pi } \over 4}} \right)\) thì y = sin x lấy mọi giá trị thuộc
A. \(\left[ {{{\sqrt 2 } \over 2};1} \right]\)
B. \( \left[ { - 1; - {{\sqrt 2 } \over 2}} \right)\)
C. \( \left[ { - {{\sqrt 2 } \over 2};0} \right]\)
D. \( \left[ { - 1;1} \right]\)
Phương pháp giải:
Tìm tập giá trị của hàm số y = sin x trên khoảng \(\left( {{{5\pi } \over 4};{{7\pi } \over 4}} \right)\).
Hướng dẫn giải:
Ta có:
\( {{5\pi } \over 4} < x < {{7\pi } \over 4} \\ \Rightarrow - 1 \le \sin x < - {{\sqrt 2 } \over 2} \\ \Rightarrow - 1 \le y < - {{\sqrt 2 } \over 2}\)
Chọn B.
16. Giải bài 58 trang 49 SGK Đại số & Giải tích 11 Nâng cao
Khi x thay đổi trong nửa khoảng \(\left( { - {\pi \over 3};{\pi \over 3}} \right]\) thì y = cos x lấy mọi giá trị thuộc:
A. \( \left[ {{1 \over 2};1} \right]\)
B. \( \left( { - {1 \over 2};{1 \over 2}} \right)\)
C. \( \left( { - {1 \over 2};{1 \over 2}} \right)\)
D. \( \left[ { - 1;{1 \over 2}} \right]\)
Phương pháp giải:
Tìm tập giá trị của hàm số y = cos x trên nửa khoảng \(\left( { - {\pi \over 3};{\pi \over 3}} \right]\).
Hướng dẫn giải:
Ta có:
\( - {\pi \over 3} < x \le {\pi \over 3} \\ \Rightarrow {1 \over 2} \le \cos x \le 1 \\ \Rightarrow {1 \over 2} \le y \le 1\)
Chọn A.
17. Giải bài 59 trang 49 SGK Đại số & Giải tích 11 Nâng cao
Số nghiệm của phương trình \(\sin \left( {x + {\pi \over 4}} \right) = 1\) thuộc đoạn [π; 2π] là
A. 1
B. 2
C. 3
D. 0
Phương pháp giải:
Giải phương trình cơ bản của sin và đếm số nghiệm thuộc đoạn [π; 2π].
Hướng dẫn giải:
Ta có:
\( \sin \left( {x + {\pi \over 4}} \right) = 1 \\ \Leftrightarrow x + {\pi \over 4} = {\pi \over 2} + k2\pi \\ \Leftrightarrow x = {\pi \over 4} + k2\pi \\ \pi \le \frac{\pi }{4} + k2\pi \le 2\pi \\\Leftrightarrow \frac{3}{8} \le k \le \frac{7}{8}\)
Do k nguyên nên không có k thỏa mãn.
Phương trình không có nghiệm thuộc [π ; 2π]
Chọn C.
18. Giải bài 60 trang 49 SGK Đại số & Giải tích 11 Nâng cao
Số nghiệm của phương trình \(\sin \left( {2x + {\pi \over 4}} \right) = - 1\) thuộc đoạn [0; π] là
A. 1
B. 2
C. 3
D. 0
Phương pháp giải:
Giải phương trình cơ bản của sin và đếm số nghiệm thuộc đoạn [0; π].
Hướng dẫn giải:
Ta có:
\( \sin \left( {2x + {\pi \over 4}} \right) = - 1 \\ \Leftrightarrow 2x + {\pi \over 4} = - {\pi \over 2} + k2\pi \\ \Leftrightarrow x = - {{3\pi } \over 8} + k\pi \\ 0 \le - \frac{{3\pi }}{8} + k\pi \le \pi \Leftrightarrow \frac{3}{8} \le k \le \frac{{11}}{8} \)
⇒ k = 1 ta được nghiệm \(x = {{5\pi } \over 8} \in \left[ {0;\pi } \right]\)
Chọn A.
19. Giải bài 61 trang 49 SGK Đại số & Giải tích 11 Nâng cao
Một nghiệm của phương trình \({\sin ^2}x + {\sin ^2}2x + {\sin ^2}3x = 2\) là
A. \( {\pi \over {12}}\)
B. \( {\pi \over {3}} \)
C. \( {\pi \over {8}}\)
D. \( {\pi \over {6}}\)
Phương pháp giải:
Thay từng giá trị ở các đáp án vào phương trình để tìm nghiệm.
Hướng dẫn giải:
Thế các đáp áp vào phương trình ta thấy \( {\pi \over {6}}\) là nghiệm của phương trình.
Chọn D.
20. Giải bài 62 trang 49 SGK Đại số & Giải tích 11 Nâng cao
Số nghiệm của phương trình \(\cos \left( {{x \over 2} + {\pi \over 4}} \right) = 0\) thuộc khoảng (π; 8π) là
A. 1
B. 3
C. 2
D. 4
Phương pháp giải:
Giải phương trình cơ bản của cos và đếm số nghiệm thuộc khoảng (π; 8π).
Hướng dẫn giải:
Ta có:
\( \cos \left( {{x \over 2} + {\pi \over 4}} \right) = 0 \\ \Leftrightarrow {x \over 2} + {\pi \over 4} = {\pi \over 2} + k\pi \\ \Leftrightarrow x = {\pi \over 2} + k2\pi \\ \pi < \frac{\pi }{2} + k2\pi < 8\pi \\ \Leftrightarrow \frac{1}{4} < k < \frac{{15}}{4}\)
Chọn \(k{\rm{ }} \in {\rm{ }}\left\{ {1;{\rm{ }}2;{\rm{ }}3} \right\}\)
Chọn B
21. Giải bài 63 trang 49 SGK Đại số & Giải tích 11 Nâng cao
Số nghiệm của phương trình \({{\sin 3x} \over {\cos x + 1}} = 0\) thuộc đoạn [2π; 4π] là
A. 2
B. 4
C. 5
D. 6
Phương pháp giải:
- Tìm ĐKXĐ.
- Giải phương trình cơ bản của sin và đếm số nghiệm thuộc đoạn [2π; 4π].
Hướng dẫn giải:
Ta có:
\( {{\sin 3x} \over {\cos x + 1}} = 0 \\ \Leftrightarrow \left\{ {\matrix{{\sin 3x = 0} \cr {\cos x \ne - 1} \cr} } \right. \\ \Leftrightarrow \left\{ {\matrix{{x = k{\pi \over 3}} \cr {x \ne \pi + k2\pi } \cr} } \right. \\ 2\pi \le x \le 4\pi \Leftrightarrow 2\pi \le \frac{{k\pi }}{3} \le 4\pi \\ \Leftrightarrow 6 \le k \le 12.\)
Cho k nhận các giá trị từ 6 đến 12 ta thấy \(x = \frac{{9\pi }}{3} = 3\pi \) có \(\cos x=-1\) nên không thỏa mãn(loại).
Chọn \(k \in {\rm{ }}\left\{ {6;{\rm{ }}7;{\rm{ }}8;{\rm{ }}10;{\rm{ }}11;{\rm{ }}12} \right\}\)
Chọn D.
