Giải bài tập SGK Toán 11 Nâng cao Bài 2: Phép tịnh tiến và phép dời hình

Qua phép tịnh tiến T theo vectơ \(\overrightarrow u\) đường thẳng d biến thành đường thẳng d’. Trong trường hợp nào thì: d trùng d’? d song song với d’? d cắt d’?

Phương pháp giải:

Tìm các vị trí của giá vectơ \(\overrightarrow u\) so với đường thẳng d và kết luận.

Hướng dẫn giải:

Nếu \(\overrightarrow u\) là vectơ chỉ phương của d thì d trùng với d’

Nếu \(\overrightarrow u\) không là vectơ chỉ phương của d thì d // d’

d không bao giờ cắt d’

Cho hai đường thẳng song song a và a’. Tìm tất cả những phép tịnh tiến biến a thành a’.

Phương pháp giải:

Lấy điểm A trên a, A' trên a'

⇒ Tìm phép tịnh tiến biến A thành A'.

Hướng dẫn giải:

Lấy điểm A trên a thì với mỗi điểm A’ trên a’, phép tịnh tiến theo vectơ \(\overrightarrow {AA'}\) biến a thành a’.

Đó là tất cả những phép tịnh tiến cần tìm

Cho hai phép tịnh tiến \({T_{\overrightarrow u }}\,\text{ và }\,{T_{\overrightarrow v }}\). Với điểm M bất kì, \({T_{\overrightarrow u }}\) biến M thành điểm M’, \({T_{\overrightarrow v }}\) biến M’ thành điểm M”. Chứng tỏ rằng phép tịnh tiến biến M thành M” là một phép tịnh tiến.

Phương pháp giải:

Biểu diễn \(\overrightarrow {MM'} \) theo hai vectơ \(\overrightarrow u\) và \(\overrightarrow v\)

Hướng dẫn giải:

Ta có:

\(\eqalign{ & {T_{\overrightarrow u }}:M \to M' \cr & {T_{\overrightarrow v }}:M' \to M \cr}\)

Suy ra \(\overrightarrow {MM'} =\overrightarrow u,\overrightarrow {M'M} = \overrightarrow v\)

Do đó \(\overrightarrow {MM} = \overrightarrow {MM'} + \overrightarrow {M'M} = \overrightarrow u + \overrightarrow v\)

Cho đường tròn (O) và hai điểm A, B. Một điểm M thay đổi trên đường tròn (O). Tìm quỹ tích điểm M’ sao cho \(\overrightarrow {MM'} + \overrightarrow {MA} = \overrightarrow {MB} .\)

Phương pháp giải:

Tính \(\overrightarrow {MM'} \) và suy ra phép tịnh tiến.

Hướng dẫn giải:

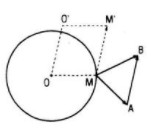
Ta có: \(\overrightarrow {MM'} = \overrightarrow {MB} - \overrightarrow {MA} = \overrightarrow {AB}\) nên phép tịnh tiến T theo vectơ \(\overrightarrow {AB}\) biến M thành M’.

Nếu gọi O’ là ảnh của O qua phép tịnh tiến T, tức \(\overrightarrow {OO'} = \overrightarrow {AB}\) thì quỹ tích M’ là đường tròn tâm O’ có bán kính bằng bán kính đường tròn (O).

Trong mặt phẳng tọa độ Oxy , với α, a, b là những số cho trước, xét phép biến hình F biến mỗi điểm M(x;y) thành điểm M′(x′;y′), trong đó:

\(\left\{ {\matrix{{x' = x\cos \alpha - y\sin \alpha + a} \cr {y' = x\sin \alpha + y\cos \alpha + b} \cr} } \right.\)

a) Cho hai điểm \(M\left( {{x_1};{y_1}} \right),\,N\left( {{x_2};{y_2}} \right)\) và gọi M', N' lần lượt là ảnh của M, N qua phép F. Hãy tìm tọa độ của M' và N'.

b) Tính khoảng cách d giữa M và N; khoảng cách d' giữa M' và N'.

c) Phép F có phải là phép dời hình hay không?

d) Khi α = 0, chứng tỏ rằng F là phép tịnh tiến.

Phương pháp giải:

a) Thay tọa độ của M và N vào phép biến hình F.

b) Áp dụng công thức tính khoảng cách \(d=AB=\sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}}\).

c) Chứng minh F bảo toàn khoảng cách giữa hai điểm M và N.

d) Thay α = 0 vào F và kết luận.

Hướng dẫn giải:

d) \(Khi\,\,\alpha = 0,\,\,\text{ ta có }\,\,\left\{ \matrix{ x' = x + a \hfill \cr y' = y + b \hfill \cr} \right.\)

Vậy F là phép tịnh tiến vectơ \(\overrightarrow u \left( {a;b} \right).\)

Trong mặt phẳng tọa độ , xét các phép biến hình sau đây:

- Phép biến hình F₁ biến mỗi điểm M (x;y) thành điểm M′ (y;−x).

- Phép biến hình F₂ biến mỗi điểm M (x;y) thành điểm M′ (2x;y).

Trong hai phép biến hình trên, phép nào là phép dời hình ?

Phương pháp giải:

- Lấy hai điểm bất kì M và N.

- Tìm ảnh M', N' của M, N qua phép biến hình F₁, F₂.

+ Nếu M'N' = MN ⇒ phép dời hình.

+ Nếu M'N' ≠ MN ⇒ không là phép dời hình.

Hướng dẫn giải:

Lấy hai điểm bất kì \(M = ({x_1};{\rm{ }}{y_1})\) và \(N = ({x_2};{\rm{ }}{y_2})\) khi đó

\(MN = \sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}}\)

Ảnh của M, N qua F1 lần lượt là \(M' = ({y_1}; - {x_1})\) và \(N' = ({y_2}; - {x_2})\)
Ta có: \(M'N' = \sqrt {{{\left( {{y_1} - {y_2}} \right)}^2} + {{\left( { - {x_1} + {x_2}} \right)}^2}}\)

⇒ M'N' = MN nên F₁ là phép dời hình.

Ảnh của M, N qua F₂ lần lượt là \(M' = (2{x_1};{\rm{ }}{y_1})\) và \(N' = (2{x_2};{y_2})\)

Ta có: \(M'N' = \sqrt {4{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}}\)

⇒ M'N' ≠ MN ⇒ F₂ không là phép dời hình.