Giải bài tập SBT Toán 11 Bài 1+Bài 2: Phép biến hình. Phép tịnh tiến

Trong mặt phẳng tọa độ Oxy cho $\vec v=(2;-1)$, điểm M = (3;2). Tìm tọa độ của các điểm A sao cho:

a) $A=T_{\vec v}(M)$;

b) $M=T_{\vec v}(A) .$

Phương pháp giải:

Sử dụng biểu thức tọa độ của phép tịnh tiến:

- Trong mặt phẳng Oxy cho điểm M(x;y) và vectơ $\vec v(a;b)$. Gọi điểm $M’=(x’;y’)=T_{\vec v}(M)$.

- Khi đó $\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.$

Hướng dẫn giải:

a) Giả sử A = (x;y) .

Theo đề cho $A=T_{\vec v}(M)$ khi đó

$\left\{ \begin{array}{l}x = 3 + 2\\y = 2 - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5\\y = 1\end{array} \right.$

Vậy A = (5;1).

b) Giả sử A = (x;y) .

Theo đề cho $M=T_{\vec v}(A)$ khi đó

 $\left\{ \begin{array}{l}3 = x + 2\\2 = y - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 3\end{array} \right.$

Vậy A = (1;3).

Trong mặt phẳng Oxy cho $\vec v=(-2;1)$, đường thẳng d có phương trình $2x-3y+3=0$, đường thẳng $d_1$ có phương trình $2x-3y-5=0$.

a) Viết phương trình của đường thẳng d’ là ảnh của d qua $T_{\vec v}$.

b) Tìm tọa độ của $\vec w$ có giá vuông góc với đường thẳng d để $d_1$ là ảnh của d qua $T_{\vec w}$.

Phương pháp giải:

a) Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó.

+ Gọi phương trình d' .

+ Lấy một điểm $A \in d$, tìm ảnh A' của A qua ${T_{\overrightarrow v }}$.

+ Cho $A' \in d'$ và suy ra phương trình của d'.

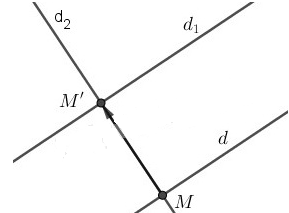
b) - Ta có $d_1=T_{\vec w}(d)$ nên $\vec w$ có điểm đầu thuộc d điểm cuối thuộc $d_1$.

- Viết phương trình đường thẳng $d_2$ đi qua 2 điểm đầu, cuối đó.

- Tìm giao của $d_2$ với d và $d_1$.

Hướng dẫn giải:

a) Lấy một điểm thuộc d, chẳng hạn M = (0;1).

Khi đó $M’=T_{\vec v}(M) =(0-2;1+1)=(-2;2) \in d’ .$

Vì d’ song song với d nên phương trình của nó có dạng $2x-3y+C=0 .$

Do $M’\in d’$ nên $2.(-2)-3.2+C=0$ từ đó suy ra C = 10.

Do đó d’ có phương trình $2x-3y+10=0 .$

b)

Lấy một điểm thuộc d, chẳng hạn M = (0;1).

Gọi đường thẳng $d_2$ qua M vuông góc với d khi đó $d_2$ có vectơ chỉ phương là $\vec v=(2;-3)$.

Do đó phương trình của $d_2$ là $\dfrac{x-0}{2}=\dfrac{y-1}{-3}$ hay $3x+2y-2=0$.

Gọi M’ là giao của $d_1$ với $d_2$ thì tọa độ của nó phải thỏa mãn hệ phương trình

$\left\{ \begin{array}{l}2x - 3y - 5 = 0\\3x + 2y - 2 = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = \dfrac{{16}}{{13}}\\y = - \dfrac{{11}}{{13}}\end{array} \right.$

Từ đó suy ra $\overrightarrow {\rm{w}} = \overrightarrow {MM'} = \left( {\dfrac{{16}}{{13}}; - \dfrac{{24}}{{13}}} \right)$.

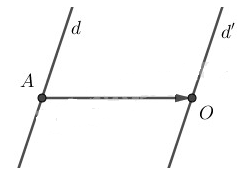
Trong mặt phẳng Oxy cho đường thẳng d có phương trình $3x-y-9=0$. Tìm phép tịnh tiến theo vectơ có phương song song với trục Ox biến d thành đường thẳng d’ đi qua gốc tọa độ và viết phương trình đường thẳng d’.

Phương pháp giải:

- Tìm điểm đầu, điểm cuối của vectơ tịnh tiến lần lượt thuộc đường thẳng d và d’.

- d' song song với d và đi qua gốc tọa độ.

Hướng dẫn giải:

Phép tịnh tiến theo vectơ có phương song song với trục Ox, do đó Ox chứa vectơ tịnh tiến.

Giao của d với trục Ox là điểm A(3;0).

Phép tịnh tiến phải tìm có vectơ tịnh tiến $\vec v=\vec {AO}=(-3;0)$.

Đường thẳng d’ song song với d và đi qua gốc tọa độ nên nó có phương trình $3x-y=0$.

Trong mặt phẳng Oxy cho đường tròn (C) có phương trình $x^2+y^2-2x+4y-4=0$. Tìm ảnh của (C) qua phép tịnh tiến theo vectơ $\vec v=(-2;5)$.

Phương pháp giải:

- Tìm tâm của đường tròn mới bằng cách sử dụng biểu thức tọa độ của phép tịnh tiến:

+ Trong mặt phẳng Oxy cho điểm M(x;y) và vectơ $\vec v(a;b)$. Gọi điểm $M’=(x’;y’)=T_{\vec v}(M)$.

+ Khi đó $\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.$.

- Bán kính của đường tròn sau khi tịnh tiến vẫn giữ nguyên.

Hướng dẫn giải:

Ta có (C) là đường tròn tâm I(1;-2), bán kính r = 3.

Gọi $I’=T_{\vec v}(I) =(1-2;-2+5)=(-1;3)$

(C’) là ảnh của (C) qua $T_{\vec v}$ thì (C’) là đường tròn tâm (I’) bán kính r = 3.

Do đó (C’) có phương trình ${(x+1)}^2+{(y-3)}^2=9 .$

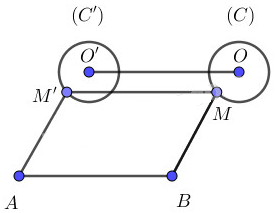
Cho đoạn thẳng AB và đường tròn (C) tâm O, bán kính r nằm về một phía của đường thẳng AB. Lấy điểm M trên (C), rồi dựng hình bình hành ABMM’. Tìm tập hợp các điểm M’ khi M di động trên (C).

Phương pháp giải:

Sử dụng định nghĩa: $T_{\vec v}(M) = M' \Leftrightarrow \overrightarrow {MM'} = \vec v$.

Hướng dẫn giải:

Do tứ giác ABMM’ là hình bình hành nên $\vec{BA}=\vec{MM’}$.

Từ đó suy ra M’ là ảnh của M qua phép tịnh tiến theo vectơ $\vec{BA}$.

Từ đó suy ra tập hợp các điểm M’ là đường tròn (C’), ảnh của (C) qua phép tịnh tiến theo vectơ $\vec {BA}$.