Giải bài tập SBT Toán 11 Bài 4: Phép đối xứng tâm
Mời các em học sinh lớp 11 cùng tham khảo nội dung giải bài tập SBT bài Phép đối xứng tâm bên dưới đây. Bài gồm có 4 bài tập được eLib sưu tầm và tổng hợp. Với nội dung chi tiết, rõ ràng giúp các em ôn tập lại các kiến thức đã học và vận dụng vào giải các bài tập tương tự. Hi vọng rằng đây sẽ là tài liệu hữu ích trong học tập của các em học sinh.
Mục lục nội dung

1. Giải bài 1.11 trang 20 SBT Hình học 11
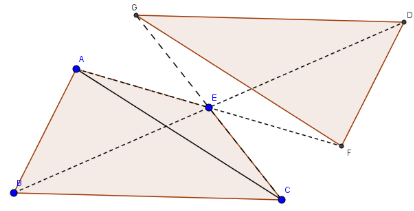
Cho tứ giác ABCE. Dựng ảnh của tam giác ABC qua phép đối xứng tâm E.
Phương pháp giải:
Dựng ảnh của từng điểm A, B, C qua phép đối xứng tâm E.
Hướng dẫn giải:
Dựng ảnh của từng điểm A, B, C qua phép đối xứng tâm E.
Gọi \(F=Đ_E(A), D=Đ_E(B), G=Đ_E(C)\).
2. Giải bài 1.12 trang 20 SBT Hình học 11
Trong mặt phẳng Oxy, cho hai điểm I(1;2), M(-2;3), đường thẳng d có phương trình 3x-y+9=0 và đường tròn (C) có phương trình: \(x^2+y^2+2x-6y+6=0\). Hãy xác định tọa độ của điểm M’, phương trình của đường thẳng d’ và đường tròn (C’) theo thứ tự là ảnh của M, d và (C) qua
a) Phép đối xứng qua gốc tọa độ;
b) Phép đối xứng qua tâm I.
Phương pháp giải:
Sử dụng biểu thức tọa độ của tâm đối xứng:
- Trong mặt phẳng tọa độ Oxy, cho \(I=(x_0; y_0)\), gọi M = (x;y) và M’ = (x’;y’) là ảnh của M qua phép đối xứng tâm I. Khi đó \(\left\{ \begin{array}{l}x' = 2{x_0} - x\\y' = 2{y_0} - y\end{array} \right. \)
- Trong câu a tâm đối xứng là O(0;0) nên \(\left\{ \begin{array}{l}x' = - x\\y' = - y\end{array} \right.\)
Hướng dẫn giải:
a) Gọi M’, d’ và (C’) theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua O.
Phép đối xứng qua gốc tọa độ nên \(\left\{ \begin{array}{l}x' = - x\\y' = - y\end{array} \right.\)
Suy ra: M’ = (2;-3)
Phương trình của d’: \(3(-x)-(-y)+9=0 \Leftrightarrow 3x-y-9=0\)
Phương trình của đường tròn (C’):
\({(-x)}^2+{(-y)}^2+2(-x)-6(-y)+6=0 \Leftrightarrow (C’): x^2+y^2-2x+6y+6=0\)
b) Gọi M’, d’ và C’ theo thứ tự là ảnh của M, d và C qua phép đối xứng qua I.
Vì I là trung điểm của MM' nên M’ = (4;1)
Vì d’ song song với d nên d’ có phương trình \(3x-y+C=0\).
Lấy N(0;9) thuộc d.
Khi đó ảnh của N qua phép đối xứng qua tâm I là N’(2;-5).
Vì N’ thuộc d nên ta có \(3.2-(-5)+C=0 \Leftrightarrow C=-11\)
Vậy phương trình của d’ là \(3x-y-11=0\).
Ta có: (C) là đường tròn tâm J(-1;3), bán kính bằng 2.
Ảnh của J qua phép đối xứng qua tâm I là J’(3;1).
Do đó (C’) là đường tròn tâm J’ bán kính bằng 2.
Phương trình của (C’) là \({(x-3)}^2+{(y-1)}^2=4\).
3. Giải bài 1.13 trang 21 SBT Hình học 11
Trong mặt phẳng Oxy, cho đường thẳng d có phương trình: \(x-2y+2=0\) và đường thẳng d’ có phương trình: \(x-2y-8=0\). Tìm phép đối xứng tâm biến d thành d’ và biến trục Ox thành chính nó.
Phương pháp giải:
- Tìm giao điểm của hai đường thẳng với Ox.
- Tâm đối xứng là trung điểm của hai giao điểm đó.
Hướng dẫn giải:
Giao của d và d’ với Ox lần lượt là A(-2;0) và A’(8;0).
Phép đối xứng qua tâm cần tìm biến A thành A’ nên tâm đối xứng của nó là I = (3;0).
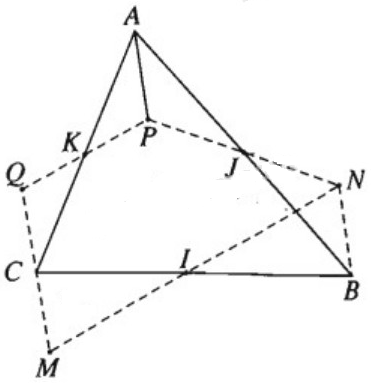
4. Giải bài 1.14 trang 21 SBT Hình học 11
Cho ba điểm không thẳng hàng I, J, K. Hãy dựng tam giác ABC nhận I, J, K lần lượt là trung điểm của các cạnh BC, AB, AC.
Phương pháp giải:
Sử dụng tính chất tâm đối xứng bảo toàn khoảng cách giữa hai điểm.
Hướng dẫn giải:
Giả sử tam giác ABC đã dựng được.
- Cách dựng điểm C:
+ Lấy điểm M bất kì.
+ Gọi N là ảnh của M qua phép đối xứng tâm I
+ Gọi P là ảnh của N qua phép đối xứng tâm J
+ Gọi Q là ảnh của P qua phép đối xứng tâm K
Khi đó \(\vec{CM}=-\vec{BN}=\vec{AP}=-\vec{CQ}\).
Do đó C là trung điểm của QM.
- Cách dựng điểm B:
+ Lấy điểm O bất kỳ
+ Gọi \(O_1\) là ảnh của O qua J
+ Gọi \(O_2\) là ảnh của \(O_1\) qua K
+ Gọi \(O_3\) là ảnh của \(O_2\) qua I
⇒ B là trung điểm của \(OO_3\).
- Cách dựng điểm A:
+ Lấy điểm H bất kỳ
+ Gọi \(H_1\) là ảnh của H qua J
+ Gọi \(H_2\) là ảnh của \(H_1\) qua K
+ Gọi \(H_3\) là ảnh của \(H_2\) qua I
⇒ A là trung điểm của \(HH_3\).
Tham khảo thêm
- doc Giải bài tập SBT Toán 11 Bài 1+Bài 2: Phép biến hình. Phép tịnh tiến
- doc Giải bài tập SBT Toán 11 Bài 3: Phép đối xứng trục
- doc Giải bài tập SBT Toán 11 Bài 5: Phép quay
- doc Giải bài tập SBT Toán 11 Bài 6: Khái niệm về phép dời hình và hai hình bằng nhau
- doc Giải bài tập SBT Toán 11 Bài 7: Phép vị tự
- doc Giải bài tập SBT Toán 11 Bài 8: Phép đồng dạng
- doc Giải bài tập SBT Hình học 11 Ôn tập chương 1: Phép dời hình và phép đồng dạng