Giải bài tập SBT Toán 11 Bài 6: Khái niệm về phép dời hình và hai hình bằng nhau

Trong mặt phẳng Oxy, cho \(\vec v=(2;0)\) và điểm M(1;1).

a) Tìm tọa độ của điểm M’ là ảnh của điểm M qua phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng qua trục Oy và phép tịnh tiến theo vectơ \(\vec v.\)

b) Tìm tọa độ của điểm M’ là ảnh của điểm M qua phép dời hình có được bằng cách thực hiện liên tiếp phép tịnh tiến theo vectơ \(\vec v\) và phép đối xứng qua trục Oy.

Phương pháp giải:

- Trong mặt phẳng tọa độ Oxy, cho đường thẳng d. Với mỗi điểm M = (x;y), gọi \(M’=Đ_d(M)=(x’;y’)\)

Nếu chọn d là trục Oy, thì \(\left\{ \begin{array}{l}x' = - x\\y' = y\end{array} \right.\)

- Trong mặt phẳng tọa độ Oxy, cho điểm M = (x;y) và vectơ \(\vec v(a;b)\). Gọi điểm \(M’(x’;y’)=T_{\vec v}(M)\).

Khi đó \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\)

Hướng dẫn giải:

a) Gọi \(N=Đ_{Oy}(M)=(-1;1), M’(x’;y’)= T_{\vec v}(N)\)

Khi đó \(\left\{ \begin{array}{l}x' = - 1 + 2\\y' = 1 + 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x' = 1\\y' = 1\end{array} \right.\)

Vậy M’ = (1;1).

b) Gọi \(N(x’;y’)= T_{\vec v}(M)\)

Khi đó \(\left\{ \begin{array}{l}x' = 1 + 2\\y' = 1 + 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x' = 3\\y' = 1\end{array} \right.\)

Như vậy \(N(x’;y’)= T_{\vec v}(M)=(3;1)\), \(M’=Đ_{Oy}(N)=(-3;1)\)

Vậy M’ = (-3;1).

Trong mặt phẳng Oxy, cho vectơ \(\vec v=(3;1)\) và đường thẳng d có phương trình \(2x-y=0\). Tìm ảnh của d qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm O góc \({90}^o\) và phép tịnh tiến theo vectơ \(\vec v\).

Phương pháp giải:

- Cho O và góc lượng giác \(\alpha\). Phép quay tâm O góc \(\alpha\).

+ Biến O thành chính nó

+ Biến mỗi điểm M khác O thành điểm M’ sao cho OM’=OM và góc lượng giác (OM;OM’) bằng \(\alpha \).

- Trong mặt phẳng tọa độ Oxy, cho điểm M=(x;y) và vectơ \(\vec v(a;b)\). Gọi điểm \(M’(x’;y’)=T_{\vec v}(M) \)

Khi đó \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\)

Hướng dẫn giải:

Gọi \(d_1\) là ảnh của d qua phép quay tâm O góc \({90}^o\).

Vì d chứa tâm quay O nên \(d_1\) cũng chứa O.

Ngoài ra \(d_1\) vuông góc với d nên \(d_1\) có phương trình \(x+2y=0\).

Gọi d’ là ảnh của \(d_1\) qua phép tịnh tiến vectơ \(\vec v\).

Khi đó phương trình của d’ có dạng \(x’-3+2(y’-1)=0 \Leftrightarrow x’+2y’-5=0.\)

Vậy phương trình d’ có dạng \(x+2y-5=0.\)

Chứng minh rằng mỗi phép quay đều có thể xem là kết quả của việc thực hiện liên tiếp hai phép đối xứng trục.

Phương pháp giải:

- Cho O và góc lượng giác \(\alpha\). Phép quay tâm O góc \(\alpha\).

+ Biến O thành chính nó

+ Biến mỗi điểm M khác O thành điểm M’ sao cho OM’=OM và góc lượng giác (OM;OM’) bằng \(\alpha \).

Hướng dẫn giải:

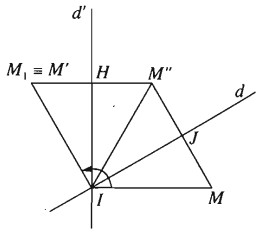
Gọi \(Q_{(I,\alpha)}\) là phép quay tâm I góc \(\alpha\).

Lấy đường thẳng d bất kì qua I.

Gọi d’ là ảnh của d qua phép quay tâm I góc \(\dfrac{\alpha}{2}\).

Lấy điểm M bất kì và gọi \(M’=Q_{(I,\alpha)}(M)\).

Gọi M’’ là ảnh của M qua phép đối xứng qua trục d. 

\(M_1\) là ảnh của M’’ qua phép đối xứng qua trục d’.

Gọi J là giao của MM’ với d, H là giao của \(M’’M_1\) với d’.

Khi đó ta có đẳng thức giữa các góc lượng giác sau:

\( (IM,IM_1) \\ =(IM,IM’’)+(IM’’,IM_1) \\ =2(IJ,IM’’)+2(IM’’,IH) \\ =2(IJ,IH) \\=2\dfrac{\alpha}{2} \\=\alpha=(IM,IM’)\)

Từ đó suy ra \(M’\equiv M_1\).

Như vậy M’ có thể xem là ảnh của M sau khi thực hiện liên tiếp hai phép đối xứng qua hai trục d và d’.

Cho hình vuông ABCD có tâm I. Trên tia BC lấy điểm E sao cho BE = AI

a) Xác định một phép dời hình biến A thành B và I thành E.

b) Dựng ảnh của hình vuông ABCD qua phép dời hình ấy. 

Phương pháp giải:

- Cho O và góc lượng giác \(\alpha\). Phép quay tâm O góc \(\alpha\).

+ Biến O thành chính nó

+ Biến mỗi điểm M khác O thành điểm M’ sao cho OM’=OM và góc lượng giác (OM;OM’) bằng \(\alpha \).

Hướng dẫn giải:

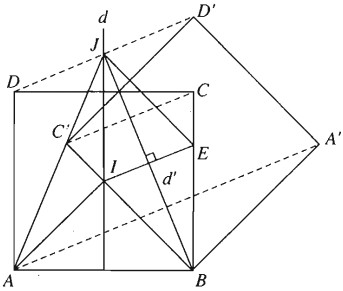
a) Gọi F là phép đối xứng qua đường trung trực d của cạnh AB, G là phép đối xứng qua đường trung trực d’ của cạnh IE.

Khi đó F biến AI thành BI, G biến BI thành BE.

Từ đó suy ra phép dời hình có được bằng cách thực hiện liên tiếp hai phép biến hình F và G  sẽ biến AI thành BE.

Hơn nữa gọi J là giao của d và d’, ta có JA = JB, JI = JE và \(2(JI,JB)=(JI,JE)={45}^o\) (vì \(JE \parallel IB\) ). 

Do đó theo kết quả của bài 1.21, phép dời hình nói trên chính là phép quay tâm J góc \({45}^o\).

b) Phép biến hình F biến các điểm A, B, C, D thành B, A, D, C ; G biến các điểm B, A, D, C thành B, A’, D’, C’.

Do đó ảnh của hình vuông ABCD qua phép dời hình nói trên là hình vuông BA’D’C’ đối xứng với hình vuông BADC qua d'.