Giải bài tập SBT Toán 11 Bài 1: Đại cương về đường thẳng và mặt phẳng

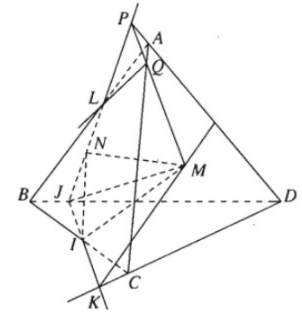
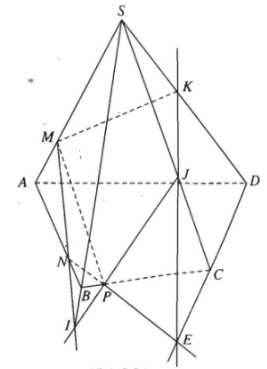
Cho tứ diện ABCD và điểm M thuộc miền trong của tam giác ACD. Gọi I và J tương ứng là hai điểm trên cạnh BC và BD sao cho IJ không song song với CD.

a) Hãy xác định giao tuyến của hai mặt phẳng (IJM) và (ACD).

b) Lấy N là điểm thuộc miền trong của tam giác ABD sao cho JN cắt đoạn AB tại L. Tìm giao tuyến của hai mặt phẳng (MNJ) và (ABC).

Phương pháp giải:

Cách xác định giao tuyến của hai mặt phẳng:

- Xác định điểm chung thứ nhất dễ nhận thấy.

- Tìm hai đường thẳng lần lượt thuộc hai mặt phẳng và chúng cắt nhau.

- Tìm giao điểm của hai đường thẳng đó ta được giao điểm thứ hai của hai mặt phẳng.

Hướng dẫn giải:

a) Nhận xét:

Trong (BCD), gọi \(K = IJ \cap CD\).

Ta có: M là điểm chung thứ nhất của (ACD) và (IJM);

\( \left\{ \matrix{ K \in IJ \hfill \cr IJ \subset \left( {MIJ} \right) \hfill \cr} \right. \Rightarrow K \in \left( {MIJ} \right) và \left\{ \matrix{K \in CD \hfill \cr C{\rm{D}} \subset \left( {AC{\rm{D}}} \right) \hfill \cr} \right. \Rightarrow K \in \left( {AC{\rm{D}}} \right)\)

Vậy \(\left( {MIJ} \right) \cap \left( {ACD} \right) = MK\)

b) Với \(L = JN \cap AB\) ta có:

\( \left\{ \matrix{ L \in JN \hfill \cr JN \subset \left( {MNJ} \right) \hfill \cr} \right. \Rightarrow L \in \left( {MNJ} \right) \\ \left\{ \matrix{ L \in AB \hfill \cr AB \subset \left( {ABC} \right) \hfill \cr} \right. \Rightarrow L \in \left( {ABC} \right) \)

Như vậy L  là điểm chung thứ nhất của hai mặt phẳng (MNJ)  và (ABC)

Gọi \(P = JL \cap A{\rm{D}},Q = PM \cap AC\)

Ta có: 

\( \left\{ \matrix{ Q \in PM \hfill \cr PM \subset \left( {MNP} \right) \hfill \cr} \right. \Rightarrow Q \in \left( {MNJ} \right)\)

Và \(\left\{ \matrix{Q \in AC \hfill \cr AC \subset \left( {ABC} \right) \hfill \cr} \right. \Rightarrow Q \in \left( {ABC} \right)\)

Nên Q là điểm chung thứ hai của (MNJ) và (ABC)

Vậy \(LQ = \left( {ABC} \right) \cap \left( {MNJ} \right).\)

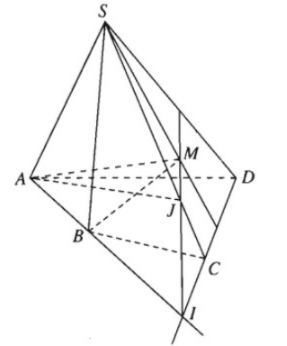
Cho hình chóp S.ABCD có đáy là tứ giác ABCD có hai cạnh đối diện không song song. Lấy điểm M thuộc miền trong của tam giác SCD. Tìm giao tuyến của hai mặt phẳng:

a) (SBM) và (SCD)

b) (ABM) và (SCD)

c) (ABM) và (SAC)

Phương pháp giải:

Cách xác định giao tuyến của hai mặt phẳng:

- Xác định điểm chung thứ nhất dễ nhận thấy.

- Tìm hai đường thẳng lần lượt thuộc hai mặt phẳng và chúng cắt nhau.

- Tìm giao điểm của hai đường thẳng đó ta được giao điểm thứ hai của hai mặt phẳng.

Hướng dẫn giải:

a) Ta có S, M là hai điểm chung mặt phẳng (SBM) và (SCD).

Vậy (SBM) \cap (SCD) = SM.

b) Ta có M là điểm chung thứ nhất

Gọi \(I = AB \cap CD\)

Khi đó \(I \in AB \Rightarrow I \in (ABM), I \in CD \Rightarrow I \in (SCD).\)

Do đó I là điểm chung thứ hai.

Vậy \((ABM) \cap (SCD) = IM.\)

c) Ta có \(A=(ABM) \cap (SAC)\)

Gọi \(J = IM \cap SC.\)

Khi đó \(J \in IM \Rightarrow J \in (ABM) \) và \( J \in SC \Rightarrow J \in (SAC).\)

Do đó \(J \in (ABM) \cap (SAC)\)

Vậy \((ABM) \cap (SAC) = AJ\)

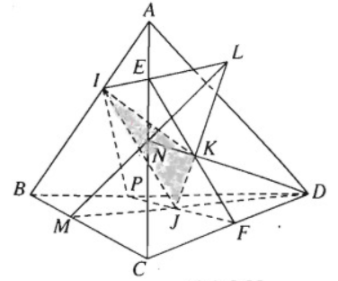
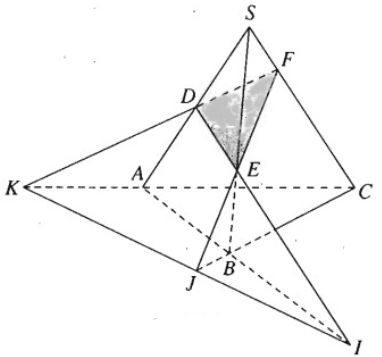
Cho tứ diện ABCD. Trên cạnh AB lấy điểm I và lấy các điểm J, K lần lượt là điểm thuộc miền trong các tam giác BCD và ACD. Gọi L là giao điểm của JK với mặt phẳng (ABC).

a) Hãy xác định điểm L

b) Tìm giao tuyến của mặt phẳng (IJK) với các mặt của tứ diện ABCD

Phương pháp giải:

a) Tìm một đường thẳng trong (ABC) có thể cắt được JK. Khi đó L là giao điểm của đường thẳng đó với JK.

b) Tìm giao tuyến của (IJK) với từng mặt của tứ diện ABCD.

Hướng dẫn giải:

a) Gọi \(N = DK \cap AC ; M = DJ \cap BC.\)

Khi đó \(MN=(DJK) \cap (ABC)\)

\( \Rightarrow MN \subset (ABC).\)

Vì \(L=JK \cap (ABC)\) nên \(L = JK \cap MN.\)

b) Ta có \(I=(IJK) \cap (ABC).\)

Mặt khác vì \(L = MN \cap JK \) mà \(MN \subset (ABC)\) và \(JK \subset (IJK)\) 

Nên L là điểm chung thứ hai của (ABC) và (IJK), suy ra \((IJK) \cap (ABC) = IL.\)

Gọi \(E = IL \cap AC ; F = EK \cap CD.\)

Khi đó \(E = (IJK) \cap (ACD) ; F = (IJK) \cap (ACD)\).

Suy ra \(EF = (IJK) \cap (ACD).\)

Nối FJ cắt BD tại P; \(P=(IJK) \cap (BCD).\)

Suy ra \(PF = (IJK) \cap (BCD) ; IP=(IJK) \cap (ABD).\)

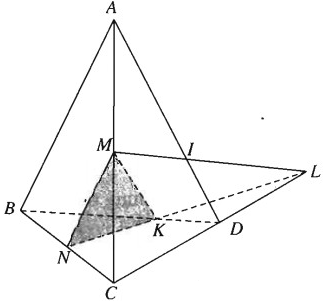
Cho tứ diện ABCD có các điểm M và N lần lượt là trung điểm của AC và BC. Lấy điểm K thuộc đoạn BD ( K không là trung điểm của BD ). Tìm giao điểm của đường thẳng AD và mặt phẳng (MNK).

Phương pháp giải:

- Xét mặt phẳng chứa AD chẳng hạn (ACD) rồi tìm giao tuyến \(\Delta\) của (ACD) với (MNK).

- Sau đó tìm giao điểm I của \(\Delta\) và AD, I chính là giao điểm phải tìm.

Hướng dẫn giải:

Gọi \(L = NK \cap CD\)

Ta có \(L \in NK \Rightarrow L \in (MNK) \\ L \in CD \Rightarrow L \in (ACD)\)

\(ML = (ACD) \cap (MNK) = \Delta \\ \Delta\cap AD = I \\ \Rightarrow I = (MNK) \cap AD.\)

Cho hình chóp S. ABCD. Lấy M, N và P lần lượt là các điểm trên các đoạn SA, AB và BC sao cho chúng không trùng với trung điểm của các đoạn thẳng ấy. Tìm giao điểm (nếu có) của mặt phẳng (MNP) với các cạnh của hình chóp.

Phương pháp giải:

Muốn tìm giao điểm của mặt phẳng \((\alpha)\) với đường thẳng d :

- Tìm đường thẳng d’ sao cho \(d’\in (\alpha)\) và d, d’ cùng thuộc một mặt phẳng.

- Giao điểm d và d’ là giao điểm của mặt phẳng \((\alpha)\) với đường thẳng d.

Hướng dẫn giải:

Ta có giao điểm của (MNP) với SA, AB, BC lần lượt là M, N, P.

Trong (SAB) kéo dài MN và SB, khi đó gọi \(I=MN\cap SB\)

Ta có:

\( \begin{array}{l}\left\{ \begin{array}{l}I \in MN,MN \subset (MNP) \Rightarrow I \in (MNP)\\I \in SB\end{array} \right.\\ \Rightarrow I = (MNP) \cap SB\end{array}\)

Trong (ABCD) kéo dài NP và kéo dài CD, khi đó gọi \(E=NP\cap CD\)

Ta có:

\( \begin{array}{l}\left\{ \begin{array}{l}E \in NP,NP \subset (MNP) \Rightarrow E \in (MNP)\\E \in CD\end{array} \right.\\ \Rightarrow E = (MNP) \cap CD\end{array}\)

Trong (MNP) hay cũng là (MIP) kéo dài IP, khi đó gọi \(J=IP\cap SC\)

Ta có:

\( \begin{array}{l}\left\{ \begin{array}{l}J \in IP,IP \subset (MNP) \Rightarrow J \in (MNP)\\J \in SC\end{array} \right.\\ \Rightarrow J = (MNP) \cap SC\end{array}\)

Trong (SCD) kéo dài EJ gọi \(K=EJ\cap SD\)

Ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}K \in {\rm{EJ}},{\rm{EJ}} \subset (MNP) \Rightarrow K \in (MNP)\\K \in SD\end{array} \right.\\ \Rightarrow K = (MNP) \cap SD\end{array}\)

Cho hình chóp S.ABCD. M và N tương ứng là các điểm thuộc các cạnh SC và BC. Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN).

Phương pháp giải:

Trong bài ta có \(SD\subset (SBD)\) như vậy mục tiêu là tìm \(d’=(AMN)\cap(SBD)\).

→ Giao điểm cần tìm là giao của SD và d’.

Hướng dẫn giải:

Gọi \(O = AC \cap BD\)

Trong (SAC) gọi \(K = SO \cap AM\)

Trong (ABCD) gọi \(L = BD \cap AN\)

Khi đó \(KL=(SBD)\cap(AMN)\)

Suy ra \(SD\cap (AMN)=SD\cap KL=P\)

Ta có \(P \in KL,KL \subset (AMN)\)

\( \Rightarrow P \in (AMN) \ và \ P \in SD \\ \Rightarrow P = (AMN) \cap SD.\)

Cho tứ diện SABC. Trên SA, SB và SC lần lượt lấy các điểm D, E và F sao cho DE cắt AB tại I, EF cắt BC tại J, FD cắt CA tại K. Chứng minh ba điểm I, J, K thẳng hàng.

Phương pháp giải:

Để chứng minh ba điểm thẳng hàng ta chứng minh ba điểm đó cùng thuộc hai mặt phẳng phân biệt.

Hướng dẫn giải:

Ta có: \(I = DE \cap AB\)

Mà \(DE \subset (DEF) \Rightarrow I \in (DEF)\)

Và \(AB \subset (ABC) \Rightarrow I \in (ABC)\)

Suy ra \(I\in (DEF)\cap (ABC)\)

Ta có: \(J = EF \cap BC\)

Mà \(EF \subset (DEF) \Rightarrow J \in (DEF)\)

Và \(BC \subset (ABC) \Rightarrow J \in (ABC)\)

Suy ra \(J\in (DEF)\cap (ABC)\)

Tương tự, \(K\in (DEF)\cap (ABC)\) nên I, J, K thuộc giao tuyến của (ABC) và (DEF) nên I, J, K thẳng hàng.

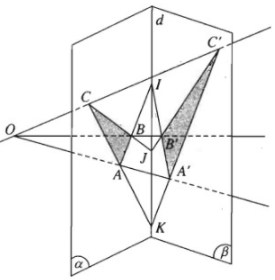
Cho hai mặt phẳng \((\alpha)\) và \((\beta)\) cắt nhau theo giao tuyến d. Trong \((\alpha)\) lấy hai điểm A và B sao cho AB cắt d tại I. O là một điểm nằm ngoài \((\alpha)\) và \((\beta)\) sao cho OA và OB lần lượt cắt \((\beta)\) tại A’ và B’.

a) Chứng minh ba điểm I, A’, B’ thẳng hàng.

b) Trong \((\alpha)\) lấy điểm C sao cho A, B, C không thẳng hàng. Giả sử OC cắt \((\beta)\) tại C’, BC cắt B’C’ tại J, CA cắt C’A’ tại K. Chứng minh I, J, K thẳng hàng.

Phương pháp giải:

Để chứng minh ba điểm thẳng hàng ta chứng minh ba điểm đó cùng thuộc hai mặt phẳng phân biệt.

Hướng dẫn giải:

a) Ta có \(AB\cap d=I\)

Khi đó \(I\in AB, AB\subset (OAB)\Rightarrow I\in (OAB) \) và \( I\in d, d\subset (\beta)\Rightarrow I\in (\beta)\)

Suy ra \(I=(OAB)\cap (\beta)\)

Ta có \(A’=OA\cap (\beta)\)

Khi đó \(A’\in OA, OA\subset (OAB)\)

\( \Rightarrow A’\in (OAB) \) và \(A’\in (\beta)\)

Suy ra \(A’=(OAB)\cap (\beta)\)

Chứng minh tương tự \(B’=(OAB)\cap (\beta)\)

Vậy I, A’, B’ là ba điểm chung của hai mặt phẳng (OAB) và \((\beta)\) nên chúng thẳng hàng.

b) Ta có \(I=AB\cap d\) khi đó \(I\in AB, AB\subset (ABC)\Rightarrow I\in (ABC)\)

Và \(I\in d, d\subset (\beta)\Rightarrow I\in (\beta)\) mà \(A’, B’, C’\in (\beta) \Rightarrow(A’B’C’)\) là \((\beta)\) nên \(I\in (A’B’C’)\)

Suy ra \(I\in (ABC)\cap (A’B’C’)\)

Ta có \(BC\cap B’C’=J\)

Khi đó \(J\in BC, BC\subset (ABC)\Rightarrow J\in (ABC)\) và \(J\in B’C’, B’C’\subset (A’B’C’)\)

\( \Rightarrow J\in (A’B’C’)\)

Suy ra \(J\in (ABC)\cap (A’B’C’)\)

Tương tự ta có \(K\in (ABC)\cap (A’B’C’)\)

Vậy I, J, K là ba điểm chung của hai mặt phẳng (ABC) và (A’B’C’) nên chúng thẳng hàng.

Cho tứ diện SABC có D, E lần lượt trung điểm AC, BC và G là trọng tâm tam giác ABC. Mặt phẳng \((\alpha)\) qua AC cắt SE, SB lần lượt tại M, N. Một mặt phẳng \((\beta)\) qua BC cắt SD và SA lần lượt tại P và Q.

a) Gọi \(I = AM \cap DN, J = BP \cap EQ\). Chứng minh bốn điểm S, I, J, G thẳng hàng.

b) Giả sử \(AN \cap DM = K, BQ \cap EP = L\). Chứng minh ba điểm S, K, L thẳng hàng.

Phương pháp giải:

Để chứng minh ba điểm thẳng hàng ta chứng minh ba điểm đó cùng thuộc hai mặt phẳng phân biệt

Hướng dẫn giải:

a) 

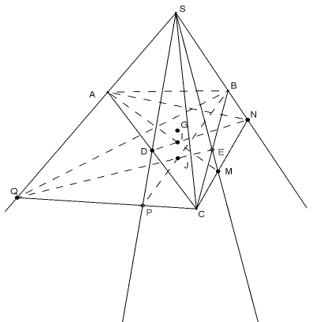
Ta thấy:

+ G là trọng tâm tam giác ABC \( \Rightarrow G \in BD \Rightarrow G \in BD.\)

+ \(I \in DN\) (theo cách dựng hình).

+ \(J \in BP\) (theo cách dựng hình).

\( \Rightarrow S, I, J, G \in (SPN)\)

Tương tự  \(S, I, J, G \in (SQM)\)

Vậy S, I, J, G là điểm chung của (SPN) và (SQM) nên chúng thẳng hàng.

b)

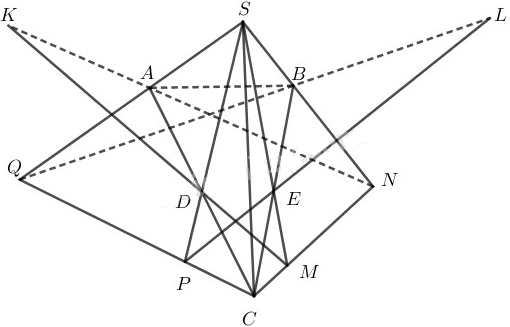
Ta thấy:

+ \(S = PD \in EM\)

+ \(K \in DM\)

+ \(L \in PE\)

\( \Rightarrow S, K, L \in (SPM)\)

Tương tự \(S, K, L \in (SQN)\)

Vậy S, K, L là điểm chung của (SPM) và (SQN) nên chúng thẳng hàng.