Giải bài tập SBT Toán 11 Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song

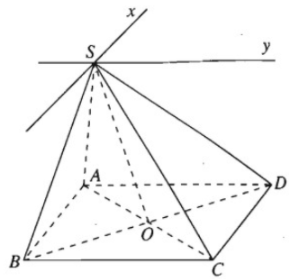
Cho hình chóp S.ABCD có đáy là hình hình hành ABCD. Tìm giao tuyến của các cặp mặt phẳng sau đây:

a) (SAC) và (SBD)

b) (SAB) và (SCD) 

c) (SAD) và (SBC).

Phương pháp giải:

a) - Tìm hai điểm chung dễ thấy nhất của (SAC) và (SBD)

- Tìm trong hai mặt phẳng hai đường thẳng có thể cắt nhau → điểm chung thứ hai.

→ Giao tuyến của (SAC) và (SBD).

b) c) Cách tìm giao tuyến của hai mặt phẳng lần lượt chứa hai đường thẳng d và d’ song song với nhau:

- Tìm điểm chung của hai mặt phẳng

- Giao tuyến của hai mặt phẳng là đường thẳng đi qua điểm chung và song song với d và d’.

Hướng dẫn giải:

a) Ta có: $S\in (SAC)\cap(SBD)$

Gọi $AC \cap BD = O$

Mà $AC\subset (SAC), BD\subset (SBD) \Rightarrow O\in (SAC)\cap(SBD)$

$\Rightarrow (SAC) \cap (SBD) = SO.$

b) Ta có: $S\in (SAB)\cap(SCD)$

Ta lại có:

$\left\{ \begin{array}{l}AB \subset (SAB)\\CD \subset (SCD)\\AB\parallel CD\end{array} \right. \\ \Rightarrow (SAB)\cap (SCD)=Sx, Sx\parallel AB\parallel CD.$

c) Ta có: $S\in (SAD)\cap(SBC)$

Ta lại có:

$\left\{ \begin{array}{l}AD \subset (SAD)\\BC \subset (SBC)\\AD\parallel BC\end{array} \right. \\ \Rightarrow (SAD)\cap (SBC)=Sy, Sy\parallel AD\parallel BC.$

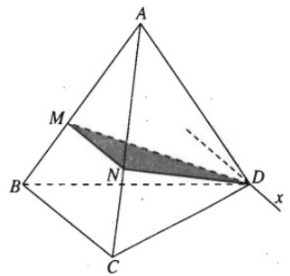
Cho tứ diện ABCD. Trên các cạnh AB và AC lần lượt lấy các điểm M và N sao cho $\dfrac{AM}{AB}=\dfrac{AN}{AC}$. Tìm giao tuyến của hai mặt phẳng (DBC) và (DMN).

Phương pháp giải:

- Chứng minh hai đường thẳng song song dựa vào Định lý Talet.

- Cách tìm giao tuyến của hai mặt phẳng lần lượt chứa hai đường thẳng d và d’ song song với nhau:

+ Tìm điểm chung của hai mặt phẳng.

+ Giao tuyến của hai mặt phẳng là đường thẳng đi qua điểm chung và song song với d và d’.

Hướng dẫn giải:

Ta có:

$M\in AB, N\in AC \Rightarrow MN\subset (ABC)$

Trong tam giác ABC ta có:

$\dfrac{AM}{AB}=\dfrac{AN}{AC} \Rightarrow MN\parallel BC$

Ta có: D ∈ (DBC) ∩ (DMN)

$\left\{ \begin{array}{l}BC \subset (DBC)\\MN \subset (DMN)\\BC\parallel MN\end{array} \right. \\ \Rightarrow (DBC)\cap (DMN)=Dx, Dx\parallel BC\parallel MN.$

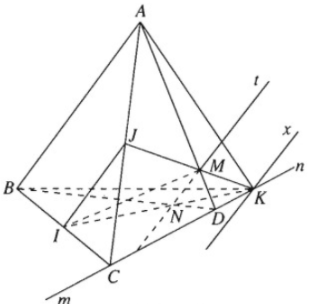
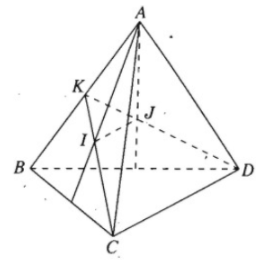
Cho tứ diện ABCD. Cho I và J tương ứng là trung điểm của BC và AC, M là một điểm tùy ý trên cạnh AD.

a) Tìm giao tuyến d của hai mặt phẳng (MIJ) và (ABD)

b) Gọi N là giao điểm của BD với giao tuyến d, K là giao điểm của IN và JM. Tìm tập hợp điểm K khi M di động trên đoạn AD (M không là trung điểm của AD).

c) Tìm giao tuyến của hai mặt phẳng (ABK) và (MIJ)

Phương pháp giải:

a) Cách tìm giao tuyến của hai mặt phẳng lần lượt chứa hai đường thẳng d và d’ song song với nhau:

- Tìm điểm chung của hai mặt phẳng.

- Giao tuyến của hai mặt phẳng là đường thẳng đi qua điểm chung và song song với d và d’.

b) Từ $K=IN\cap JM$ của giả thiết ta suy ra được K là giao của hai mặt phẳng.

Sử dụng tính chất “Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng sẽ có một đường thẳng chung đi qua điểm chung ấy” suy ra được K thuộc giao tuyến của hai mặt phẳng.

c) Cách tìm giao tuyến của hai mặt phẳng lần lượt chứa hai đường thẳng d và d’ song song với nhau:

- Tìm điểm chung của hai mặt phẳng.

- Giao tuyến của hai mặt phẳng là đường thẳng đi qua điểm chung và song song với d và d’.

Hướng dẫn giải:

a) Ta có:

$M\in (MIJ)$ và $M\in AD, AD\subset (ABD)$

$\Rightarrow M\in (ABD) \Rightarrow M\in (MIJ)\cap (ABD)$

Ta cũng có:

$\left\{ \begin{array}{l}{\rm{IJ}}\parallel AB\\{\rm{IJ}} \subset (M{\rm{IJ}})\\AB \subset (ABD)\end{array} \right. \\ \Rightarrow (MIJ)\cap(ABD)=d=Mt, Mt\parallel AB\parallel IJ.$

b) Trong (ABD) có $Mt \parallel AB \Rightarrow Mt \cap BD = N$

$IN\cap JM=K$

Khi đó $K ∈ IN, IN\subset (BCD)$

$\Rightarrow K ∈ (BCD)$

và $K ∈ JM, JM\subset (ACD)$

 ⇒ K ∈ (ACD)

$\Rightarrow K\in (BCD)\cap(ACD)$

Mặt khác $(BCD) \cap (ACD) = CD$ 

Do đó $K \in CD$.

Do vậy K nằm trên hai nửa đường thẳng Cm và Dn thuộc đường thẳng CD.

c) Ta có:

$\begin{array}{l}\left\{ \begin{array}{l}K \in (ABK)\\K \in IN,IN \subset (M{\rm{IJ}})\end{array} \right.\\ \Rightarrow K \in (ABK) \cap (M{\rm{IJ}})\end{array}$

Mà

$\left\{ \begin{array}{l}AB \subset (ABK)\\{\rm{IJ}} \subset (M{\rm{IJ}})\\AB\parallel {\rm{IJ}}\end{array} \right.\\ \Rightarrow (ABK) \cap (M{\rm{IJ}}) = Kx, Kx\parallel AB\parallel {\rm{IJ}}.$

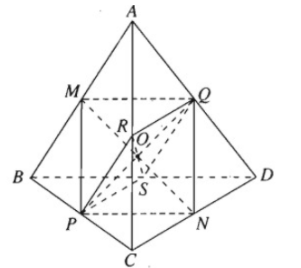
Cho tứ diện ABCD. Gọi M, N, P, Q, R và S lần lượt trung điểm của AB, CD, BC, AD, AC và BD. Chứng minh rằng tứ giác MPNQ là hình bình hành. Từ đó suy ra ba đoạn thẳng MN, PQ và RS cắt nhau tại trung điểm mỗi đoạn.

Phương pháp giải:

Chứng minh MNPQ, PRQS là hình bình hành → đpcm.

Hướng dẫn giải:

Trong tam giác ABC ta có: MP // AC và $MP = \dfrac{AC}{2}.$

Trong tam giác ACD ta có: QN // AC và $QN = \dfrac{AC}{2}.$

Từ đó suy ra $\left\{ \begin{array}{l}MP\parallel QN\\ MP = QN\end{array} \right.$

⇒ Tứ giác MPNQ là hình bình hành.

Do vậy hai đường chéo MN và PQ cắt nhau tại trung điểm O  của mỗi đường.

Tương tự: PR //l QS và $PR = QS = \dfrac{AB}{2}.$

Do đó tứ giác PRQS là hình bình hành.

Suy ra hai đường chéo PQ và RS cắt nhau tại trung điểm O của PQ và OR = OS

Vậy ba đoạn thẳng MN, PQ và RS cắt nhau tại trung điểm mỗi đoạn.

Cho tứ diện ABCD có I và J lần lượt là trọng tâm các tam giác ABC và ABD. Chứng minh rằng: IJ // CD.

Phương pháp giải:

Chứng minh $\dfrac{{KI}}{{KC}} = \dfrac{{KJ}}{{KD}}$ bằng tính chất trọng tâm

→ IJ // CD.

Hướng dẫn giải:

Gọi K là trung điểm của AB.

Vì I là trọng tâm của tam giác ABC nên $I \in KC$ và vì J là trọng tâm của tam giác ABD nên $J \in KD$.

Từ đó suy ra trong tam giác CKD ta có

$\dfrac{{KI}}{{KC}} = \dfrac{{KJ}}{{KD}} = \dfrac{1}{3} \Rightarrow {\rm{IJ}}\parallel CD.$

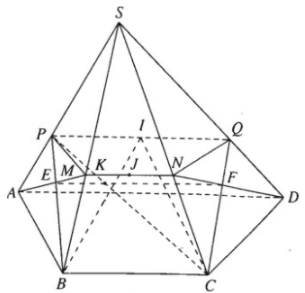
Cho hình chóp S.ABCD có đáy là hình thang ABCD với đáy là AD và BC. Biết AD = a, BC = b. Gọi I và J lần lượt là trọng tâm của các tam giác SAD và SBC. Mặt phẳng (ADJ) cắt SB, SC lần lượt tại M, N. Mặt phẳng (BCI) cắt SA, SD lần lượt tại P, Q.

a) Chứng minh MN song song với PQ.

b) Giả sử AM cắt BP tại E; CQ cắt DN tại F. Chứng minh rằng EF song song với MN và PQ. Tính EF theo a và b. 

Phương pháp giải:

a) Chứng minh MN và BC cùng song song với đường thẳng khác.

b) - Chứng minh EF = (AMND) ∩ (PBCQ) → EF // MN // PQ.

- Áp dụng định lý Talet cho các cặp đường thẳng song song để tính EF.

Hướng dẫn giải:

a) Ta có: I ∈ (SAD) ⇒ I ∈ (SAD) ∩ (IBC)

Mà

$\begin{array}{l}\left\{ \begin{array}{l}AD\parallel BC\\AD \subset (SAD)\\BC \subset (IBC)\end{array} \right.\\ \Rightarrow (SAD) \cap (IBC) = {\rm{Ix}} = PQ;\end{array} PQ \parallel AD \parallel BC$

Tương tự: J ∈ (SBC) ⇒ J ∈ (SBC) ∩ (JAD)

Mà

$\begin{array}{l}\left\{ \begin{array}{l}AD\parallel BC\\AD \subset (JAD)\\BC \subset (SBC)\end{array} \right.\\ \Rightarrow (JAD) \cap (SBC) = J{\rm{x}} = MN;\end{array} MN\parallel BC\parallel AD$

Suy ra PQ // MN (vì cùng song song với AD, BC ).

b) Ta có: $E = AM \cap BP$

Khi đó $E \in AM,AM \subset (AMND) \Rightarrow E \in (AMND)$

$E \in BP,BP \subset (PBCQ) \Rightarrow E \in (PBCQ)$

Suy ra $E\in (AMND)\cap(PBCQ).$

$F = DN \cap CQ$

Khi đó $F \in DN,DN \subset (AMND)$

$\Rightarrow F \in (AMND)\\F \in CQ,CQ \subset (PBCQ) \\ \Rightarrow F \in (PBCQ)$

Suy ra $F\in (AMND)\cap(PBCQ)$

Do đó: EF = (AMND) ∩ (PBCQ)

Mà AD // BC và MN // PQ suy ra EF // AD // BC // MN // PQ

Tính EF: $CP \cap EF = K ⇒ EF = EK + KF$

${\rm{EF}}\parallel BC \Rightarrow \dfrac{{EK}}{{BC}} = \dfrac{{PE}}{{PD}}\\PM\parallel AB \Rightarrow \dfrac{{PE}}{{EB}} = \dfrac{{PM}}{{AB}}$

Mà $\dfrac{{PM}}{{AB}} = \dfrac{{SP}}{{SA}} = \dfrac{2}{3}$

$\Rightarrow \dfrac{{PE}}{{EB}} = \dfrac{2}{3}$

Suy ra

$\dfrac{{EK}}{{BC}} = \dfrac{{PE}}{{PB}} = \dfrac{{PE}}{{PE + EB}} = \dfrac{1}{{1 + \dfrac{{EB}}{{PE}}}} = \dfrac{1}{{1 + \dfrac{3}{2}}} = \dfrac{2}{5}\\ \Rightarrow EK = \dfrac{2}{5}BC = \dfrac{2}{5}b$

Tương tự ta tính được $KF = \dfrac{2}{5}a$

Vậy ${\rm{EF}} = \dfrac{2}{5}a + \dfrac{2}{5}b = \dfrac{2}{5}(a + b).$