Giải bài tập SGK Vật lý 11 Nâng cao Bài 3: Điện trường

Chọn phát biểu sai.

A. Điện phổ cho phép ta nhận biết sự phân bố các đường sức của điện trường.

B. Đường sức điện có thể là đường cong kín.

C. Cũng có khi đường sức điện không xuất phát từ điện tích dương mà xuất phát từ vô cùng.

D. Các đường sức của điện trường đều là các đường thẳng song song và cách đều nhau.

Phương pháp giải

Để trả lời câu hỏi này cần nắm được các đặc điểm của về điện phổ của điện trường

Hướng dẫn giải

- Đường sức điện trường là những đường cong không kín.

- Chọn B

Chọn phương án đúng.

Công thức xác định cường độ điện trường của điện tích điểm Q < 0 có dạng:

\(\begin{array}{l} A.\,\,E = {9.10^9}\frac{Q}{{{r^2}}}\\ B.\,\,E = - {9.10^9}\frac{Q}{{{r^2}}}\\ C.\,\,E = {9.10^9}\frac{Q}{r}\\ D.\,\,E = - {9.10^9}\frac{Q}{r} \end{array}\)

Phương pháp giải

Áp dụng công thức:

\(E = {9.10^9}.\frac{{\left| Q \right|}}{{{r^2}}}\) với Q < 0

Hướng dẫn giải

- Công thức xác định cường độ điện trường của điện tích điểm Q < 0 có dạng:

\(E = {9.10^9}.\frac{{\left| Q \right|}}{{{r^2}}} = - {9.10^9}.\frac{Q}{{{r^2}}}\)

(vì Q < 0 nên |Q|=−Q)

- Chọn B

Một điện tích thử đặt tại điểm có cường độ điện trường 0,16 V/ m. Lực tác dụng lên điện tích đó bằng 2.10^-4 N. Hỏi độ lớn của điện tích đó là bao nhiêu?

Phương pháp giải

Tính độ lớn của điện tích theo công thức:

\(|q| = \frac{F}{E}\)

Hướng dẫn giải

Ta có: E = 0,16 (V/m); F = 2.10^-4 (N)

Theo công thức: 

\(\begin{array}{l} E = \frac{F}{{|q|}}\\ \Rightarrow |q| = \frac{F}{E} = \frac{{{{2.10}^{ - 4}}}}{{0,16}} = {1,25.10^{ - 3}}(C) \end{array}\)

Có một điện tích Q = 5.10^-9 C đặt tại điểm A trong chân không. Xác định cường độ điện trường tại điểm B cách A một khoảng 10 cm.

Phương pháp giải

Áp dụng công thức: 

\(E = {9.10^9}.\frac{{\left| Q \right|}}{{{r^2}}}\) để tính cường độ điện trường

Hướng dẫn giải

Q = 5.10^-9 (C)

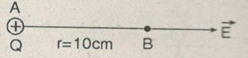
Ta có:  

\(E = {9.10^9}\frac{{|Q|}}{{{r^2}}} = \frac{{{{9.10}^9}{{.5.10}^{ - 9}}}}{{{{(0,1)}^2}}} = 4500(V/m)\)

Có hai điện tích q₁, q₂ đặt cách nhau 10 cm trong chân không. Điện tích q₁= 5.10^-9 C, điện tích q₂ = -5.10^-9 C. Xác định cường độ điện trường tại điểm M nằm trên đường thẳng đi qua hai điện tích đó và :

a) Cách đều hai điện tích;

b) Cách q₁ một khoảng 5cm và cách q₂ một khoảng 15cm.

Phương pháp giải

Áp dụng công thức:

\(E = {9.10^9}.\frac{{\left| Q \right|}}{{{r^2}}}\)

để tính cường độ điện trường với mỗi khoảng cách tương ứng

Hướng dẫn giải

a) 

q₁ = 5.10_-9(C) AB = 10cm

q₂ = -5.10-9(C) => r1 = r2 = 5(cm) 

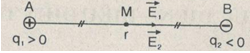
Cường độ điện trường do q1, q2 gây ra tại M

\({E_1} = {9.10^9}\frac{{|{q_1}|}}{{{r_1}^2}} = \frac{{{{9.10}^9}{{.5.10}^{ - 9}}}}{{{{({{5.10}^{ - 2}})}^2}}} = 18000(V/m).\)

Ta có: độ lớn E= E₁+E₂= 2E₁( vì E₁=E₂)

⇒E=36000(V/m), \(\vec E\) hướng về phía q₂

b)

Độ lớn:

\(\begin{array}{l} E = {E_1} - {E_2} = {9.10^9}\frac{{|{q_1}|}}{{N{A^2}}} - {9.10^9}\frac{{|{q_2}|}}{{N{B^2}}}\\ = {9.10^9}.\frac{{{{5.10}^{ - 9}}}}{{{{\left( {{{5.10}^{ - 2}}} \right)}^2}}} - {9.10^9}.\frac{{{{5.10}^{ - 9}}}}{{{{\left( {{{15.10}^{ - 2}}} \right)}^2}}}\\ = 16000{\mkern 1mu} {\mkern 1mu} \left( {V/m} \right) \end{array}\)

\(\vec E\) hướng ra xa q₁

Hai điện tích q₁ = q₂ = 5.10^-16 C được đặt cố định tại hai đỉnh B, C của một tam giác đều cạnh là 8cm. Các điện tích đặt trong không khí.

a) Xác định cường độ điện trường tại đỉnh A của tam giác nói trên.

b) Câu trả lời sẽ thay đổi thế nào nếu q₁= 5.10^-16 C, q₂ = -5.10^-16 C ?

Phương pháp giải

- Vẽ hình để xác định E tổng hợp theo quy tắc: cùng dấu thì đẩy nhau, trái dấu thì hút nhau

- Áp dụng công thức: 

​\(E = {9.10^9}.\frac{{\left| Q \right|}}{{{r^2}}}\)​ để tính điện trường

- Áp dụng hình vẽ để tính độ lớn của E theo E₁, E₂

Hướng dẫn giải

a)  

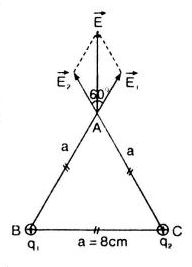
q₁ = q₂ = 5.10^-16 (C) ; AB = AC

=> E₁ = E₂

Theo hình vẽ ta có:

\(\begin{array}{l} E = 2{E_1}cos{30^o}\\ \Rightarrow E = 2.(\frac{{{{9.10}^9}{{.5.10}^{ - 16}}}}{{{{(0,08)}^2}}})cos{30^o} = 0,0012(V/m) \end{array}\)

Phương của \(\vec E\) vuông góc BC và hướng ra xa trung điểm của BC

 b)

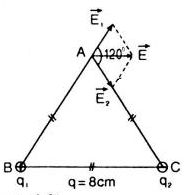
Theo hình vẽ ta có :

\(\begin{array}{l} E = 2{E_1}cos{60^o} = 2{E_1}.\frac{1}{2}\\ \Rightarrow E = 2{E_1}cos{60^o} = 2{E_1}.\frac{1}{2} \end{array}\)

Phương của \(\vec E\) song song với BC và hướng sang phải.

Ba điện tích q giống nhau được đặt cố định tại ba đỉnh của một tam giác đều cạnh a. Xác định cường độ điện trường tại tâm của tam giác.

Phương pháp giải

- Vẽ hình để xác định E tổng hợp theo quy tắc: cùng dấu thì đẩy nhau, trái dấu thì hút nhau

- Áp dụng hình vẽ để tính độ lớn của E theo E₁, E₂, E₃

Hướng dẫn giải

Tại O cách đều 3 đỉnh A, B, C với cùng độ lớn điện tích là q.

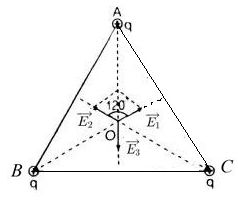
⇒ E₁=E₂=E₃

Vì \(\left( {\widehat {{{\vec E}_1},{{\vec E}_2}}} \right) = {120^0} \Rightarrow {E_{12}} = {E_1} = {E_2}\)

Với: \({{\vec E}_0} = {{\vec E}_{12}} + {{\vec E}_3}\)

\({{\vec E}_{12}}\) ngược hướng và có cùng độ lớn với \({{\vec E}_3}\)

\( \Rightarrow {{\vec E}_0} = 0\)