Giải bài tập SGK Vật lý 11 Nâng cao Bài 54: Kính thiên văn

Trong các trường hợp sau, trường hợp nào sử dụng kính thiên văn khúc xạ để quan sát rõ vật là đúng?

A. Thay đổi khoảng cách giữa vật kính và thị kính bằng cách giữ nguyên vật kính, dịch chuyển thị kính sao cho nhìn thấy ảnh của vật to và rõ nhất.

B. Thay đổi khoảng cách giữa vật và kính bằng cách dịch chuyển kính so với vật sao cho nhìn thấy ảnh của vật to và rõ nhất.

C. Thay đổi khoảng cách giữa vật kính và thị kính bằng cách giữ nguyên thị kính, dịch chuyển vật kính sao cho nhìn thấy ảnh của vật to và rõ nhất.

D. Dịch chuyển thích hợp cả vật kính và thị kính sao cho nhìn thấy ảnh của vật to và rất nhỏ.

Phương pháp giải

Sử dụng lít thuyết về kính thiên văn để trả lời câu hỏi này

Hướng dẫn giải

- Khi sử dụng kính thiên văn khúc xạ để quan sát rõ vật ta hay đổi khoảng cách giữa vật kính và thị kính bằng cách giữ nguyên vật kính, dịch chuyển thị kính sao cho nhìn thấy ảnh của vật to và rõ nhất.

- Chọn A

Vật kính của một kính thiên văn học sinh có tiêu cự f1 = 1,2m; thị kính là thấu kính hội tụ có tiêu cự f2= 4cm. Tính khoảng cách giữa hai kính và số bội giác của kính thiên văn trong trường hợp ngắm chừng ở vô cực.

Phương pháp giải

- Khoảng cách giữa hai kính được tính bằng công thức:

O1O2 = d'1 + d2=f1+ f2

- Công thức tính sô bội giác là: 

G_∞=f1/f2

Hướng dẫn giải

Kính thiên văn khúc xạ có f₁= 1,2 (m), f₂= 4 cm, ngắm chừng ở vô cực.

Theo sơ đồ tạo ảnh:

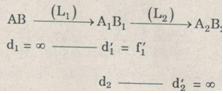
\({d_2}^\prime = \infty \Rightarrow {d_2} = {f_2}\)

- Khoảng cách giữa vật kính và thị kính:

O1O2 = d'1 + d2=f1+ f2=120 + 4= 124 cm.

- Số bội giác là:

\( \Rightarrow {G_\infty } = \frac{{{f_1}}}{{{f_2}}} = \frac{{120}}{4} = 30\)

Một kính thiên văn khúc xạ được điều chỉnh cho một người có mắt bình thường nhìn được ảnh rõ nét của vật ở vô cực mà không phải diều tiết. Khi đó vật kính và thị kính cách nhau 62 cm và số bội giác G = 30. 

a) Xác định tiêu cự của vật kính và thị kính.

b) Vật quan sát là Mặt Trăng có góc trông α₀=(1100)rad. Tính đường kính của Mặt Trăng cho bởi vật kính.

Phương pháp giải

a) Áp dụng công thức:

O1O₂=f1+f2 và G_∞=f1/f2 để tính tiêu cự

b) Tính đường kính bằng công thức:

\({{A_1}{B_1} = {\alpha _0}f}\)

Hướng dẫn giải

Kính thiên văn khúc xạ ngắm chừng ở vô cực có G∞=30 và khoảng cách giữa vật kính và thị kính O1O₂ = 62 cm

a) Ta có: 

+ O1O₂=f1+f2=62

+ G_∞=f1/f2=30

Giải hệ phương trình ta được: f₁= 60 (cm) và f₂ = 2 (cm)

b) Góc trông Mặt Trăng α₀=1100(rad)

Ta có: 

\(\begin{array}{l} \tan {\alpha _0} = \frac{{{A_1}{B_1}}}{{{f_1}}} \approx {\alpha _0}\\ \Rightarrow {A_1}{B_1} = {\alpha _0}{f_1} = 60.\frac{1}{{100}} = 0,6cm \end{array}\)

Vậy đường kính của ảnh Mặt Trăng cho bởi vật kính là 0,6 cm

Năm 1610, Ga-li-lê đã quan sát thấy 4 vệ tinh của Mộc tinh. Ganymede là một trong 4 vệ tinh đó và là vệ tinh lớn nhất trong số các vệ tinh của các hành tinh trong hệ Mặt Trời. Đường kính xích đạo của nó khoảng 5262km. Nếu Ga-li-lê muốn quan sát thấy vệ tinh này khi nó cách xa Trái Đất là 630 000 000 km thì ông phải dùng kính thiên văn có số bội giác ít nhất là bao nhiêu?

Phương pháp giải

- Áp dụng công thức:

\(\tan {\alpha _0} = \frac{{AB}}{l}\) để tính góc trông vật

- Số bội giác của kính thiên văn được tính bằng công thức:

\(G = \frac{\alpha }{{{\alpha _o}}}\)

Hướng dẫn giải

- Góc trông α₀ khi quan sát vệ tinh Ganymede của Mộc Tinh.

\(\begin{array}{l} \tan {\alpha _0} = \frac{{AB}}{l} \\ = \frac{{5262}}{{630000000}} = {8,35.10^{ - 6}}rad\\ \Rightarrow {\alpha _0} \approx {8,35.10^{ - 6}}rad \end{array}\)

- Để trông thấy vệ tinh qua kính thiên văn thì α≥ 1 phút = 3.10^-4rad.

\( \Rightarrow G = \frac{\alpha }{{{\alpha _0}}} \ge \frac{{{{3.10}^{ - 4}}}}{{{{8,35.10}^{ - 4}}}} \Rightarrow G \ge 35,92\)