Giải bài tập SGK Vật lý 11 Nâng cao Bài 45: Phản xạ toàn phần

Chọn câu trả lời đúng.

Cho một tia sáng đi từ nước (n=4/3) ra không khí. Sự phản xạ toàn phần xảy ra khi góc tới:

A. i < 49°                      C. i> 49°.

B. i>42°                        D. i > 43°

Phương pháp giải

Vận dụng công thức: sini_gh=n₂/n₁ để tính góc giới hạn

Hướng dẫn giải

- Ta có sini_gh=n₂/n₁=1:4/3=3/4⇒i_gh=49⁰ và i>igh

- Chọn C

Câu nào dưới đây không đúng ?

A. Ta luôn luôn có tia khúc xạ khi tia sáng đi từ môi trường có chiết suất nhỏ hơn sang môi trường có chiết suất lớn hơn.

B. Ta luôn luôn có tia khúc xạ khi tia sáng đi từ môi trường có chiết suất lớn hơn sang môi trường có chiết suất nhỏ hơn.

C. Khi chùm sáng phản xạ toàn phần thì không có chùm sáng khúc xạ.

D. Khi có sự phản xạ toàn phần, cường độ chùm sáng phản xạbàng cường độ chùm sáng tới.

Phương pháp giải

Để trả lời câu hỏi này cần nắm được đặc điểm về sự phản xạ toàn phần

Hướng dẫn giải

- B là câu trả lời sai. Vì khi ánh sáng đi vào môi trường có chiết suất nhỏ hơn thì chỉ có tia khúc xạ nếu góc tới i < i_gh

- Chọn B

Một khối thuỷ tinh P có chiết suất n = 1,5, tiết diện thẳng là một tam giác cân ABC vuông góc tại B. Chiếu vuông góc tới mặt AB một chùm sáng song song SI

a) Khối thuỷ tinh P ở trong không khí. Tính góc D làm bởi tia ló và tia tới.

b) Tính lại góc D nếu khối P ở trong nước có chiết suất n’ =1,33.

Phương pháp giải

a) Áp dụng công thức: sini_gh=n₂/n₁ để tính góc gới hạn

⇒ có hiện tượng phản xạ toàn phần nên góc lệch là 90°

b)- Tương tự, tìm góc giới hạn với n' =1,33

⇒ có hiện tượng khúc xạ vì  i = 45° < i_gh 

- Áp dụng định luật khúc xạ: \(\sin {\mkern 1mu} r = \frac{{{n_1}}}{{{n_2}}}\sin i\) để tính góc r

- Góc lệch D tính theo công thức: D = r - i

Hướng dẫn giải

a)

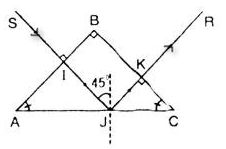
Tia tới SI⊥AB, góc tới i = 0 nên góc khúc xạ bằng 0, do đó tia SI truyền thẳng đến gặp mặt AC giữa thuỷ tinh và không khí, lúc này ta có trường hợp tia sáng đi từ thuỷ tinh ra không khí.

Góc giới hạn i_gh được tính theo công thức:

\(\begin{array}{l} \sin {i_{gh}} = \frac{{{n_2}}}{{{n_1}}} = \frac{{{n_{kkhi}}}}{{{n_{ttinh}}}} = \frac{1}{{1,5}}\\ \Rightarrow {i_{gh}} = {41,8^0} \end{array}\)

Ta có góc tới i = 45° > igh nên có hiện tượng phản xạ toàn phần tại mặt AC.

Vậy góc lệch D giữa tia ló KR và tia tới SI là 90°.

b)

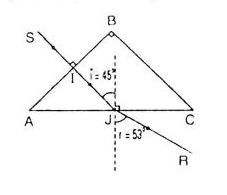
Nếu khối thuỷ tinh ở trong nước thì:

\(\begin{array}{l} \sin {i_{gh}} = \frac{{{n_2}}}{{{n_1}}} = \frac{{{n_{nuoc}}}}{{{n_{ttinh}}}} = \frac{{1,33}}{{1,5}}\\ \Rightarrow {i_{gh}} = {62,5^0} \end{array}\)

Lúc này góc tới i = 45° < i_gh, ta có hiện tượng khúc xạ ánh sáng:

\(\begin{array}{l} \frac{{\sin i}}{{{\rm{sin}}{\mkern 1mu} {\rm{r}}}} = \frac{{{n_2}}}{{{n_1}}}\\ \Rightarrow \sin {\mkern 1mu} r = \frac{{{n_1}}}{{{n_2}}}\sin i = \frac{{1,5}}{{1,33}}\sin {45^0}\\ \Rightarrow r = {53^0} \end{array}\)

Góc lệch D giữa tia ló và tia tới là.

D = 53° - 45° = 8°.

Một miếng gỗ mỏng hình tròn, bán kính 4cm. Người ta cắm thẳng góc một chiếc đinh qua tâm O của miếng gỗ nổi trong chậu nước. Thành chậu thẳng đứng và rìa miếng gỗ cách thành chậu 10cm. Nước có chiết suất n = 1,33

a) Cho OA = 6cm. Mắt ở trong không khí sẽ thấy đầu A cách mặt nước trong không khí bao nhiêu?

b) Tìm chiều dài lớn nhất của OA để mắt không thấy đầu A của đinh.

c) Thay nước bằng một chất lỏng có chiết suất n Khi giảm chiều dài OA của đinh tới 3,2cm thì mắt không thấy được đầu A của đinh nữa. Tính n’.

Phương pháp giải

a) Áp dụng định luật khúc xạ cùng hình vẽ, ta rút ra được:

\({OA' = \frac{{{n_2}}}{{{n_1}}}OA}\)

b) Dựa vào hình vẽ và công thức tính góc giới hạn: sini_gh=n₂/n₁

ta tìm được đoạn OA là: \(OA = \frac{4}{{\tan {{49}^0}}} \)

c)- Áp dụng hình vẽ và công thức tính góc giới hạn, ta tìm được:

\(\begin{array}{l} \cot gi = \frac{1}{{\tan i}} \end{array}\)

- Áp dụng công thức lượng giác để tìm n'

Hướng dẫn giải

a)

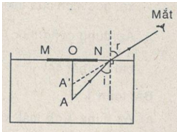
Mắt ở trong không khí sẽ thấy tia khúc xạ từ nước ra không khí, do đó mắt quan sát thấy ảnh A' của A.

\(\begin{array}{l} \frac{{OA'}}{{{n_2}}} = \frac{{OA}}{{{n_1}}}\\ \Rightarrow OA' = \frac{{{n_2}}}{{{n_1}}}OA = \frac{1}{{1,33}}.6 = 4,5\left( {cm} \right) \end{array}\)

Vậy mắt ở trong không khí sẽ thây đầu A cách mặt nước 4,5 cm.

 b) Để mắt không thây đầu A của dinh thì i > i_gh vì lúc dó không có tia khúc xạ từ nước ra không khí. Chiều dài lớn nhất của OA thoả i = i_gh và đồng thời phải bị cạnh của miếng gỗ che lấp đi.

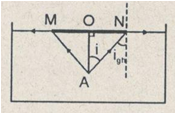
Ta có: \(\tan i = \frac{{ON}}{{OA}} \Rightarrow OA = \frac{{ON}}{{\tan i}}\)

Với \(sin{i_{gh}} = \frac{{{n_2}}}{{{n_1}}} = \frac{1}{{1,33}} \Rightarrow {i_{gh}} = {49^0}\)

Vậy: \(OA = \frac{4}{{\tan {{49}^0}}} = 3,53\left( {cm} \right)\)

c) Khi thay nước bằng một chất lỏng có chiết suất n' thì khi chiều dài của đinh là 3,2 cm thì mắt cũng không nhìn thấy đầu A của đinh.

Tương tự như câu trên: i=i_gh với sini_gh=n₂/n₁=1/n′

\(\begin{array}{l} OA = \frac{R}{{tani}}\\ \Rightarrow \tan i = \frac{R}{{OA}} = \frac{4}{{3,2}} = 1,25\\ \Rightarrow \cot gi = \frac{1}{{\tan i}} = 0,8 \end{array}\)

Áp dụng công thức lượng giác:

\(\begin{array}{l} 1 + cot{g^2}i = \frac{1}{{{{\sin }^2}i}}\\ \Rightarrow 1 + {0,8^2} = {n^{\prime 2}} \Rightarrow n' = 1,28 \end{array}\)