Giải bài tập SGK Vật lý 11 Nâng cao Bài 4: Công của lực điện. Hiệu điện thế

Chọn phương án đúng.

Một điện tích q chuyển động trong điện trường (đều hay không đều) theo một đường cong kín. Gọi công của lực điện trong chuyển động đó là A thì

A. A > 0 nếu q > 0.

B. A > 0 nếu q < 0.

C. A  0 nếu điện trường không đều.                       

D. A = 0.

Phương pháp giải

Điện tích khi chuyển động tròn điện trường theo một đường cong kín thì không sinh công

Hướng dẫn giải

- Một điện tích q chuyển động trong điện trường (đều hay không đều) theo một đường cong kín tức là điểm đầu và điểm cuối trùng nhau, nên A = 0

- Chọn D

Chọn phương án đúng.

Cho ba điểm M, N, P trong một điện trường đều. MN = 1cm ; NP=3cm; U_MN = 1V; U_MP = 2V. Gọi cường độ điện trường tại M, N, P là E_M, E_N, E_P.

A.E_N>E_M                                 B.E_P=2E_N

C.E_P=3E                                 D. E_P=E_N

Phương pháp giải

Cường độ điện trường tại mọi điểm trong điện trường đều là như nhau

Hướng dẫn giải

- Vì là điện trường đều nên E bằng nhau tại mọi điểm

E_P=E_N

- Chọn D

Một điện tích q chuyển động từ điểm M đến điểm N, từ điểm N đến điểm p như trên hình 4.4 thì công của lực điện trong mỗi trường hợp bằng bao nhiêu? Giải thích.

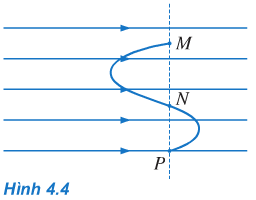
Phương pháp giải

Vận dụng tính chất: "Công của lực điện trường chỉ phụ thuộc điểm đầu và điểm cuối, do đó công trên các khoảng bằng nhau là như nhau và chỉ khác nhau về dấu" để giải bài này

Hướng dẫn giải

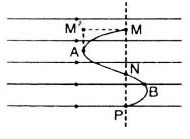
Chia quãng đường MN làm 2 phần MA và AN bằng nhau, công của lực điện trường trong mỗi đoạn có độ lớn bằng nhau và trái dấu nên cộng tổng cộng từ M đến N bằng 0

\({A_{MN}} = qE\overline {MM'} + qE\overline {M'M} = 0\)

Tương tự cho quãng đường NP⇒A_NP=0

Hai tấm kim loại phẳng rộng đặt song song, cách nhau 2cm, được nhiễm điện trái dấu nhau và có độ lớn bằng nhau. Muốn điện tích q=5.10^-10 C di chuyển từ tấm này đến tấm kia cần tốn một công A = 2.10^-9 J. Hãy xác định cường độ điện trường bên trong hai tấm kim loại đó. Cho biết điện trường bên trong hai tấm kim loại đã cho là điện trường đều và có đường sức vuông góc với các tấm.

Phương pháp giải

Áp dụng công thức: E = Ad/q để tính cường độ điện trường

Hướng dẫn giải

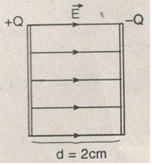
Cường độ điện trường là:

\(\begin{array}{l} A = qEd\\ \Rightarrow E = \frac{A}{{qd}} = \frac{{{{2.10}^{ - 9}}}}{{{{5.10}^{ - 10}}.0,02}} = 200(V/m) \end{array}\)

Một êlectron chuyển động dọc theo đường sức của một điện trường đều. Cường độ diện trường E = 100 V/ m. Vận tốc ban đầu của êlectron bằng 300km/s. Hỏi êlectron chuyển động được quãng đường dài bao nhiêu thì vận tốc của nó bằng không? Cho biết khối lượng êlectron m=9,1.10^-31kg.

Phương pháp giải

- Áp dụng các công thức:

+ F = ma để suy ra a

 \(+ V - {V_o}^2 = 2aS\\\) để suy ra S

- Từ đó ta rú ra được công thức tính quãng đường là:

\({S = \frac{{m{V_0}^2}}{{2qE}}}\)

Hướng dẫn giải

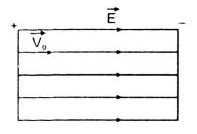
Lực điện trường tác dụng lên êlectron \(\vec F\) ngược hướng \(\vec E\) đóng vai trò lực cản.

Ta có:  

\(\begin{array}{l} \vec F = m\vec a \Leftrightarrow - qE = ma\\ \Rightarrow a = \frac{{ - qE}}{m} \end{array}\)

Lại có:

\(\begin{array}{l} V - {V_o}^2 = 2aS\\ 0 - {V_0}^2 = 2aS\\ \Rightarrow S = - \frac{{{V_0}^2}}{{2a}} = \frac{{m{V_0}^2}}{{2qE}} \end{array}\)

Thay số:

\(S = \frac{{{{9,1.10}^{ - 31}}.{{({{3.10}^5})}^2}}}{{{{2.1,6.10}^{ - 19}}.100}} = 0,0026(m)\)

Vậy S=2,6 (mm)

Hiệu điện thế giữa hai điểm M, N là U_MN = 1V. Một điện tích q = -1C di chuyển từ M đến N thì công của lực điện bằng bao nhiêu. Giải thích ý nghĩa của kết quả tính được.

Phương pháp giải

- Áp dụng công thức: A=qU để tính công của lực điện

- Vận dụng lí thuyết về công của lực điện để giải thích kết quả

Hướng dẫn giải

U_MN =1(V); q = -1(C)

- Điện tích điểm chuyển từ M đến N thì công của lực điện là:

A=qU=−1(J)

Ý nghĩa: 

+ Điện tích dương di chuyển từ nơi có điện thế cao đến nơi có điện thế thấp hơn. (Lực điện sinh công A > 0).

+ Điện tích âm di chuyển từ nơi có điện thế thấp đến nơi có điện thế cao hơn. (lực điện sinh công A > 0).

Một quả cầu nhỏ khối lượng 3,06.10^-15 kg nằm lơ lửng giữa hai tấm kim loại song song nằm ngang và nhiễm điện trái dấu. Điện tích của quả cầu đó bằng 4,8.10^-18 C. Hai tấm kim loại cách nhau 2cm. Hãy tính hiệu điện thế đặt vào hai tấm dó. Lấy g = 10m/s² 

Phương pháp giải

- Cho lực điện và trọng lượng của vật bằng nhau, ta suy ra được công thức: mg=qE

- Áp dụng công thức tính cường độ điên trường: E= U/q

- Tính hiệu điện thế theo công thức là:

\(U = \frac{{mgd}}{q}\)

Hướng dẫn giải

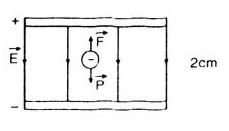
Khi quả cầu nằm lơ lửng giữa hai tấm kim loại thì trọng lực tác dụng lên quả cầu cân bằng với lực điện.

- Ta có:

\(\vec P + \vec F = 0 \Rightarrow P = F \Rightarrow mg = qE\)

Mà: E = U/d

\( \Rightarrow mg = q\frac{U}{d}\)

\( \Rightarrow U = \frac{{mgd}}{q} = \frac{{{{3,06.10}^{ - 15}}{{.10.2.10}^{ - 2}}}}{{{{4,8.10}^{ - 18}}}} = 127,5(V)\)

 Vậy hiệu điện thế là 127,5V

Một quả cầu khối lượng 4,5.10^-3 kg treo vào một sợi dây dài 1m. Quả cầu nằm giữa hai tấm kim loại song song, thẳng đứng như hình vẽ. Hai tấm cách nhau 4cm. Đặt một hiệu điện thế 750V vào hai tấm đó thì quả cầu lệch ra khỏi vị trí ban đầu 1cm. Tính điện tích của quả cầu. Lấy g = 10m/s².

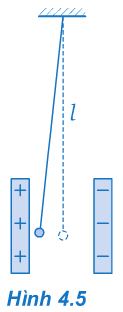
Phương pháp giải

- Phân tích lực đối với quả cầu

- Từ hình vẽ, ta tìm được tỉ số của F/P=tanα 

- Áp dụng tính chất góc α nhỏ, rút ra được công thức tính điện tích là:
\(q = \frac{{mgds}}{{Ul}}\)

Hướng dẫn giải

Quả cầu đứng yên, ta có sự cân bằng giữa các lực căng dây \(\vec T\), trọng lực \(\vec P\)và lực điện \(\vec F\)

\(\vec P\: + \vec F\: + \:\vec T = 0\:\:\)

Ta có: 

\(\tan \alpha = \frac{F}{P} = \frac{{qE}}{{mg}} = \frac{{qU}}{{mgd}}\)

Với góc α nhỏ ⇒ tanα ≈ α ≈ s/l

\(\Rightarrow \frac{s}{l} = \frac{{qU}}{{mgd}} \Rightarrow q = \frac{{mgds}}{{Ul}}\)

 Thay số:

\(|q| = \frac{{{{4,5.10}^{ - 3}}{{.10.4.10}^{ - 2}}{{.10}^{ - 2}}}}{{750.1}} = {2,4.10^{ - 8}}(C)\)