Giải bài tập SGK Vật lý 11 Nâng cao Bài 47: Lăng kính
Nội dung hướng dẫn Giải bài tập Lý 11 Nâng cao Bài 47 dưới đây sẽ giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức về lăng kính. Mời các em cùng theo dõi.
Mục lục nội dung

1. Giải bài 1 trang 233 SGK Vật lý 11 Nâng cao
Chọn phương án dứng.
Một tia sáng tới vuông góc với mặt AB của một lăng kính có chiết suất n=√2 và góc ở đỉnh A= 30°, B là góc vuông. Góc lệch của tia sáng qua lăng kính là:
A. 5° B. 13°
C. 15° D. 22°
Phương pháp giải
- Áp dụng công thức:
\({\rm{sinr}} = \frac{{{n_1}\sin i}}{{{n_2}}}\) để tính góc r
- Góc lệch được tính theo công thức: D=r-A
Hướng dẫn giải
- Ta có:
\(\begin{array}{l} i = {30^0}\\ \Rightarrow {\rm{sinr}} = \frac{{{n_1}\sin i}}{{{n_2}}} = \frac{{\sqrt 2 \sin {{30}^0}}}{1} = \frac{{\sqrt 2 }}{2}\\ \Rightarrow r = {45^0} \end{array}\)
Góc lệch D = 45° - 30° = 15°
- Chọn C
2. Giải bài 2 trang 233 SGK Vật lý 11 Nâng cao
Chọn phương án đúng.
Chiếu một chùm sáng song song tới lăng kính. Cho góc tới i tăng dần từ giá trị nhỏ nhất thì:
A. góc lệch D tăng theo i
B. góc lệch D giảm dần.
C. góc lệch D tăng tới một giá trị xác định rồi giảm dần.
D. góc lệch D giảm tới một giá trị xác định rồi tăng dần.
Phương pháp giải
Để trả lời câu hỏi này cần nắm được tính chất của tia ló khi đi qua lăng kính
Hướng dẫn giải
- Chiếu một chùm sáng song song tới lăng kính cho góc i tăng dần từ giá trị nhỏ nhất thì góc lệch D giảm tới một giá trị xác định rồi tăng dần
- Chọn D
3. Giải bài 3 trang 233 SGK Vật lý 11 Nâng cao
Phát biểu nào dưới đây không chính xác?
Chiếu một chùm tia sáng vào một mặt bên của một lăng kính ở trong không khí:
A. góc khúc xạ r bé hơn góc tới i.
B. góc tới r’ tại mặt bên thứ hai bé hơn góc ló i’
C. luôn luôn có chùm tia sáng ló ra ở mặt bên thứ hai.
D. Chùm tia sáng bị lệch khi đi qua lăng kính.
Phương pháp giải
Lăng kính chỉ cho góc ló khi chiếu góc tới nhỏ hơn góc giới hạn của lăng kính
Hướng dẫn giải
- C là phát biểu không chính xác. Vì ta chỉ có chùm tia sáng ló ra ở mặt bên thứ hai nếu góc tới nhỏ hơn góc giới hạn của lăng kính.
- Chọn C
4. Giải bài 4 trang 234 SGK Vật lý 11 Nâng cao
Khảo sát và vẽ đường đi tia sáng trong trường hợp tia tới là là trên mặt lăng kính.
Phương pháp giải
- Áp dụng công thức: sinr=1/n để tính góc r
- Tính góc r' theo công thức: r' = A - r
- Tính góc ló i' theo công thức:
\({in\left( {A - r} \right) = \frac{1}{n}sini'}\)
- Áp dụng công thức lượng giác để tính góc i' và vẽ hình
Hướng dẫn giải
- Trong trường hợp tia tới là là trên mặt lăng kính, ta có góc tới i≈900 theo công thức sini = nsinr
\( \Rightarrow {\rm{sinr}} = \frac{{\sin i}}{n} = \frac{{\sin {{90}^0}}}{n} = \frac{1}{n}\)
⇒ r bằng góc giới hạn của lăng kính ⇒ r = igh
- Góc tới r' = A - r = A - igh
- Góc ló i':
\(\begin{array}{l} sini' = nsinr' = nsin\left( {A - r} \right)\\ = > sin\left( {A - r} \right) = \frac{1}{n}sini' \end{array}\)
- Dùng công thức lượng giác:
\(\begin{array}{l} \sin A\cos r - \sin {\rm{rcosA}} = \frac{{\sin i'}}{n}\\ \Leftrightarrow \sin A.\sqrt {1 - {\rm{si}}{{\rm{n}}^2}{\rm{r}}} - \sin r\cos A = \frac{{\sin i'}}{n}\\ \Leftrightarrow \sin A.\sqrt {1 - \frac{1}{{{n^2}}}} - \frac{1}{n}{\rm{cosA}} = \frac{{\sin i'}}{n}\\ \Leftrightarrow \sin A.\frac{{\sqrt {{n^2} - 1} }}{n} - \frac{1}{n}{\rm{cosA}} = \frac{{\sin i'}}{n} \end{array}\)
Từ đây ta tìm dược góc i' và vẽ tia ló.
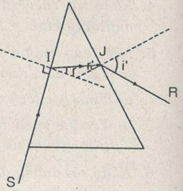
5. Giải bài 5 trang 234 SGK Vật lý 11 Nâng cao
Một lăng kính thuỷ tinh có chiết suất n = 1,5; tiết diện chính là một tam giác đều, được đặt trong không khí.
a) Tính góc lệch của tia sáng qua lăng kính khi góc tới là 30°.
b) Vẽ đường đi tia sáng và tính góc mà tia ló hợp với tia tới trong trường hợp tia tới vuông góc với mặt bên của lăng kính.
Phương pháp giải
a) Để tính góc lệch ta làm các bước sau:
- Tính r theo công thức: sinr=sini/n
- Tìm r'=A - r
- Tìm i' theo công thức \(\sin i' = n\sin r'\)
- Tính góc lệch theo công thức: D = i + i' - A
b)- Đối với tia sáng đi từ không khí vào lăng kính:
Áp dụng công thức: sinr=sini/r để tính r
⇒ Tia IJ truyền thẳng đến mặt AC.
- Đối với tia sáng đi từ lăng kính ra không khí
Áp dụng công thức:
\(\sin {i_{gh}} = \frac{{{n_2}}}{{{n_1}}}\)
⇒ Có sự phản xạ toàn phần
Hướng dẫn giải
a) Ta có A = 60°, n = 1,5; lăng kính đặt trong không khí.
Ta có: i=30°
\(\begin{array}{l} \Rightarrow {\rm{sinr}} = \frac{{{\rm{sini}}}}{n} = \frac{{\sin {{30}^0}}}{{1,5}} = 0,333\\ \Rightarrow r = {19^0}{28^\prime }\\ \end{array}\)
r' = A - r = 60 - 19°28' = 40°32'
\( \Rightarrow \sin i' = n\sin r'\)
⇒i'= 77°
Vậy góc lệch D = i + i' - A = 30° + 77° - 60° = 47°
b)
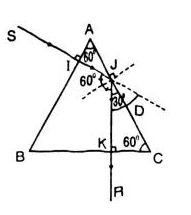
Trường hợp cho tia tới SI vuông góc với mặt bên lăng kính
- Tia sáng đi từ không khí vào lăng kính:
n1= 1, n2= 1,5
SI⊥AB ⇒ i = 0°
\( \Rightarrow {\rm{sinr}} = \frac{{\sin i}}{{{n_2}}} = \frac{0}{{1,5}} = 0 \Rightarrow r = 0\)
⇒ Tia IJ truyền thẳng đến mặt AC.
- Tia sáng đi từ lăng kính ra không khí:
n1= 1,5, n2= 1
- Ta có:
\(\sin {i_{gh}} = \frac{{{n_2}}}{{{n_1}}} = \frac{1}{{1,5}} \Rightarrow {i_{gh}} = {42^{0.}}\)
- Góc tới i = 60° >igh nên có sự phản xạ toàn phần, tia JK là tia phản xạ.
- Tia sáng đi từ lăng kính ra không khí: n1= 1,5, n2= 1
- Ta có tia tới JK⊥BC nên i = 0 ⇒ r = 0
- Tia ló KR truyền thẳng ra ngoài không khí
Dựa vào hinh vẽ ta tính được góc lệch D = 60°.
6. Giải bài 6 trang 234 SGK Vật lý 11 Nâng cao
Khảo sát đường đi của tia sáng qua lăng kính trong hai trường hợp sau:
a) Lăng kính có góc ở đinh là A = 50°, chiết suất n=√2 đặt trong nước có chiết suất n′=4/3, góc tới là i = 45 .
b) Lăng kính thuỷ tinh đặt trong không khí có góc ở đính A = 75°, góc C = 60°, chiết suất n =1,5, góc tới của tia sáng là i = 30°. Tia tới đến mặt AB của lăng kính.
Phương pháp giải
Để khảo sát đường đi của tia sáng qua lăng kính, ta giải theo phương pháp như sau:
- Xét từng cặp môi trường tới (n1) và môi trường khúc xạ (n2).
+ Nếu n1< n2: khúc xạ ánh sáng kiểu (cụp), vẽ r < i.
+ Nếu n1> n2: phải tính igh theo công thức sinigh=n2/n1, sau đó so sánh với góc tới r'.
+ r’ < igh khúc xạ (kiểu xoè), vẽ r' > r.
+ r' = igh tia khúc xạ là là với mặt lăng kính.
+ r' > igh phản xạ toàn phần, vẽ tia phản xạ với góc phản xạ bằng với góc tới r" = r'.
- Cách làm tương tự cho câu a và câu b
Hướng dẫn giải
a) Tia sáng đi từ nước (n1=4/3)→ lăng kính (n2=√2)
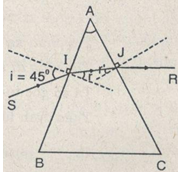
Ta có: n1< n2, theo định luật khúc xạ ánh sáng
\(\begin{array}{l} {\rm{sinr}} = \frac{{{n_1}\sin i}}{{{n_2}}} = \frac{{\frac{4}{3}\sin {{45}^0}}}{{\sqrt 2 }}\\ \Rightarrow r = {41^0}{48^\prime } \end{array}\)
Tia khúc xạ là IJ đến mặt AC.
- Tia sáng đi từ lăng kính (n1=√2)→ nước (n2=4/3)
( n1 > n2 )
\(\begin{array}{l} \sin {i_{gh}} = \frac{{{n_2}}}{{{n_1}}} = \frac{{\frac{4}{3}}}{{\sqrt 2 }}\\ \Rightarrow {i_{gh}} = {70^0}{31^\prime } \end{array}\)
- Góc tới r' = A - r = 50° - 41°48' = 8° 12' < igh
- Theo định luật khúc xạ ánh sáng:
\(\begin{array}{l} \sin i' = \frac{{{n_1}{\rm{sin}}{{\rm{r}}^\prime }}}{{{n_2}}} = \frac{{\sqrt 2 \sin {8^0}{{12}^\prime }}}{{\frac{4}{3}}}\\ \Rightarrow i' = {8^0}{42^\prime } \end{array}\)
Góc lệnh D = i + i' - A = 45° + 8°42' - 50 = 3°42'
b)Tia sáng đi từ không khí (n1= 1) vào lăng kính (n2 = 1,5), ta có n1< n2.
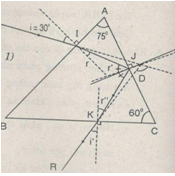
- Theo định luật khúc xạ ánh sáng:
\(\begin{array}{l} sinr = \frac{{{n_1}\sin i}}{{{n_2}}} = \frac{{\sin {{30}^0}}}{{1,5}}\\ \Rightarrow r = {19^0}{30^\prime } \end{array}\)
⇒ Tia khúc xạ là IJ đến mặt AC.
- Ta có:
\(\sin {i_{gh}} = \frac{{{n_2}}}{{{n_1}}} = \frac{1}{{1,5}} \Rightarrow {i_{gh}} = {42^0}\)
- Góc tới r' = A - r = 75° - 19°30' = 55°30'
r' > igh ⇒ phản xạ toàn phần.
⇒ Tia phản xạ JK trên mặt AC đến mặt BC.
- Ta có: góc tới r" = C - r' = 60° - 55°30' = 4°30'
- Theo định luật khúc xạ ánh sáng:
\(\begin{array}{l} \sin i' = \frac{{{n_1}\sin r''}}{{{n_2}}} = 1,5\sin {4^0}{30^\prime }\\ \Rightarrow i' = {6^0}{45^\prime } \end{array}\)
- Góc lệch D = 81°45'
7. Giải bài 7 trang 234 SGK Vật lý 11 Nâng cao
Lăng kính có góc ở đỉnh là 60°. Chùm sáng song song qua lăng kính có độ lệch cực tiểu là Dm=42°. Hãy tìm góc tới và chiết suất của lăng kính.
Phương pháp giải
- Áp dụng công thức:
\({\sin \frac{{{D_m} + A}}{2} = n\sin \frac{A}{2}}\) để tính chiết suất
- Áp dụng công thức:
\(i = \frac{{{D_m} + A}}{2}\) để tính góc tới
Hướng dẫn giải
Lăng kính có A = 60°, Dm= 42°
- Chiết suất của lăng kính là:
\(\begin{array}{l} \sin \frac{{{D_m} + A}}{2} = n\sin \frac{A}{2}\\ = \sin \frac{{{{60}^0} + {{42}^0}}}{2} = n\sin \frac{{{{60}^0}}}{2}\\ \Rightarrow n = \frac{{\sin {{51}^0}}}{{\sin {{30}^0}}} = 1,55 \end{array}\)
- Góc tới là:
\(i = \frac{{{D_m} + A}}{2} = \frac{{{{42}^0} + {{60}^0}}}{2} = {51^0}\)
Tham khảo thêm
- doc Giải bài tập SGK Vật lý 11 Nâng cao Bài 48: Thấu kính mỏng
- doc Giải bài tập SGK Vật lý 11 Nâng cao Bài 50: Mắt
- doc Giải bài tập SGK Vật lý 11 Nâng cao Bài 51: Các tật của mắt và cách khắc phục
- doc Giải bài tập SGK Vật lý 11 Nâng cao Bài 52: Kính lúp
- doc Giải bài tập SGK Vật lý 11 Nâng cao Bài 53: Kính hiển vi
- doc Giải bài tập SGK Vật lý 11 Nâng cao Bài 54: Kính thiên văn
- doc Giải bài tập SGK Vật lý 11 Nâng cao Bài 56: Thực hành: Xác định chiết suất của nước và tiêu cự của thấu kính phân kì
