Toán 11 Chương 1 Bài 1: Phép biến hình

- Định nghĩa: Phép biến hình là một quy tắc để với mỗi điểm M của mặt phẳng xác định được một điểm duy nhất M’ của mặt phẳng, điểm M’ gọi là ảnh của điểm M qua phép biến hình đó.

- Nếu kí hiệu phép biến hình đó là \(F\) thì ta viết \(F(M) = M'\) hay \(M' = F(M)\) và gọi điểm \(M'\) là ảnh của điểm \(M\) hay \(M\) là điểm tạo ảnh của \(M'\) qua phép biến hình \(F\).

Chú ý: Đối với phép biến hình:

• Mỗi điểm \(M\) chỉ có một ảnh \(M'\) duy nhất
• Có thể có nhiều điểm khác nhau cùng có chung một ảnh.

- Nếu \(H\) là một hình nào đó trong mặt phẳng ta kí hiệu \(H' = F(H)\) là tập hợp các điểm \(M' = F(M)\), với mọi điểm \(M\) thuộc \(H\). Khi đó ta nói \(F\) biến hình \(H\) thành \(H'\), hay hình \(H'\) là ảnh của hình \(H\) qua phép biến hình \(F\)

- Để chứng minh hình \(H'\) là ảnh của hình \(H\) qua phép biến hình \(F\) ta chứng minh rằng \(M ∈ H ⇔ F(M)∈ H'\)

- Thực hiện liên tiếp hai phép biến hình sẽ được một phép biến hình. Phép biến hình này còn được gọi là hợp thành của hai phép biến hình đã cho.

- Phép biến hình biến mỗi điểm M thành chính nó được gọi là phép đồng nhất.

Câu 1. Cho đường thẳng d. M là một điểm nằm ngoài đường thẳng d. Xác định M’ là hình chiếu vuông góc của M trên d. Đây có phải là một phép biến hình hay không?

Hướng dẫn giải

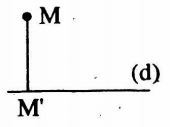
Phép biến hình này gọi là phép chiếu vuông góc lên đường thẳng d.

Câu 2. Cho vectơ \(\overrightarrow u ,\) một điểm M không nằm trên \(\overrightarrow u ,\).  Xác định điểm M’ theo quy tắc \(\overrightarrow {MM'}  = \overrightarrow u .\) Đây có phải là một phép biến hình hay không?

Hướng dẫn giải

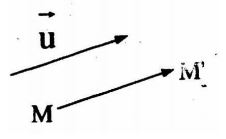
Như vậy ta cũng có một phép biến hình. Phép biến hình đó gọi là phép tịnh tiến theo vectơ \(\overrightarrow u .\)  

Câu 1: Cho trước số a dương, với mỗi điểm M trong mặt phẳng, gọi M’ là điểm sao cho MM’ = a. Quy tắc đặt tương ứng điểm M với điểm M’ nêu trên có phải là một phép biến hình không?

Câu 2: Cho tam giác ABC có trực tâm H, nội tiếp đường tròn (O), BC cố định, I là trung điểm của BC. Khi A di động trên (O), xác định ảnh của O qua phép tịnh tiến theo vectơ \(\overrightarrow v \).

Câu 1: Phép biến hình biến điểm M thành điểm M' thì với mỗi điểm M có:

A.  Ít nhất một điểm M’ tương ứng

B. Không quá một điểm M’ tương ứng

C. Vô số điểm M’ tương ứng

D. Duy nhất một điểm M’ tương ứng

Câu 2: Cho tam giác ABC nội tiếp đường trong (O). Qua O kẻ đường thẳng d. Quy tắc nào sau đây là một phép biến hình.

A. Quy tắc biến O thành giao điểm của d với các cạnh tam giác ABC

B. Quy tắc biến O thành giao điểm của d với đường tròn O

C. Quy tắc biến O thành hình chiếu của O trên các cạnh của tam giác ABC

D. Quy tắc biến O thành trực tâm H, biến H thành O và các điểm khác H và O thành chính nó

Câu 3: Trong mp Oxy cho điểm M(2;3). Điểm nào sau đây là ảnh của M qua phép đối xứng qua đường thẳng x-y=0:

A. (2;3)

B. (-2;3)

C. (2;-3)

D. (3;-2

Câu 4: Trong các phép biến hình sau,phép nào không phải là phép dời hình:

A. Phép chiếu vuông góc lên đường thẳng

B. Phép đồng nhất

C. Phép vị tự tỉ số -1

D. Phép đối xứng trục

Qua bài học này, các em cần nắm được những nội dung sau:

• Nắm được định nghĩa phép biến hình
• Xác định được ảnh của một hình qua phép biến hình.