Toán 11 Chương 1 Bài 2: Phép tịnh tiến
Sau đây mời các em học sinh lớp 11 cùng tìm hiểu về bài Phép tịnh tiến. Bài giảng dưới đây đã được eLib biên soạn khái quát lý thuyết cần nhớ, đồng thời có các bài tập được tổng hợp đầy đủ các dạng toán liên quan giúp các em dễ dàng nắm được kiến thức trọng tâm của bài.
Mục lục nội dung

1. Tóm tắt lý thuyết
1.1. Định nghĩa
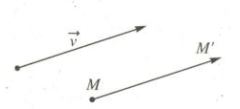
Trong mặt phẳng, cho vectơ \(\overrightarrow v = \left( {a;b} \right)\) . Phép tịnh tiến theo vectơ \(\overrightarrow v = \left( {a;b} \right)\) là phép biến hình, biến một điểm M thành một điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow v .\)
Ký hiệu: \({T_{\overrightarrow v }}(M) = M'\) hoặc \({T_{\overrightarrow v }}:M \to M'\).\(\)\(\)\(\)
1.2. Các tính chất của phép tịnh tiến
a) Tính chất 1
Định lý 1: Nếu phép tịnh tiến biến hai điểm M, N thành hai điểm M’, N’ thì MN=M’N’.
b) Tính chất 2
Định lý 2: Phép tịnh tiến biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự của ba điểm đó.
Hệ quả: Phép tịnh tiến biến đường thẳng thành đường thẳng, biến một tia thành một tia, biến một đoạn thẳng thành một đoạn thẳng bằng nó, biến một tam giác thành một tam giác bằng nó, biến một đường tròn thành một đường tròn có cùng bán kính , biến một góc thành một góc bằng nó .
1.3. Biểu thức tọa độ của phép tịnh tiến
Giả sử cho \(\overrightarrow v = \left( {a;b} \right)\) và một điểm M(x;y).
Phép tịnh tiến theo vectơ \(\overrightarrow v \) biến điểm M thành điểm M’ thì M’ có tọa độ là: \(\left\{ \begin{array}{l}x' = a + x\\y' = y + b\end{array} \right.\)
2. Bài tập minh họa
Câu 1. Trong mặt phẳng Oxy, tìm ảnh A’, B’ của điểm A(2;3), B(1;1) qua phép tịnh tiến theo vectơ \({\rm{\vec u = (3;1)}}.\) Tính độ dài các vectơ \(\overrightarrow {{\rm{AB}}} {\rm{ }},{\rm{ }}\overrightarrow {{\rm{A'B'}}} {\rm{ }}.\)
Hướng dẫn giải
Ta có:
\({\rm{A' = }}{{\rm{T}}_{{\rm{\vec u}}}}(A) = (5;4){\rm{ }}{\rm{, B' = }}{{\rm{T}}_{{\rm{\vec u}}}}(B) = (4;2){\rm{ }} \\ \Rightarrow {\rm{AB = }}\left| {\overrightarrow {{\rm{AB}}} } \right|\, = \sqrt 5 \\ \Rightarrow \left| {\overrightarrow {{\rm{A'B'}}} } \right|\, = \sqrt 5 {\rm{ }}{\rm{.}}\)
Câu 2. Đường thẳng d cắt Ox tại A(-4;0), cắt Oy tại B(0;5). Viết phương trình tham số của d’ là ảnh của d qua phép tịnh tiến theo vectơ \(\overrightarrow v = \left( {5;1} \right).\)
Hướng dẫn giải
Đường thẳng d có một VTCP là: \(\overrightarrow {{u_d}} = \overrightarrow {AB} = (4;5)\)
Vì \({T_{\overrightarrow v }}(d) = d' \Rightarrow \overrightarrow {{u_d}'} = \overrightarrow {{u_d}} = (4;5)\)
Gọi
\({T_{\overrightarrow v }}(A) = A' \Rightarrow \left\{ \begin{array}{l}{x_{A'}} = {x_A} + 5 = 1\\{y_{A'}} = {y_A} + 1 = 1\end{array} \right. \\ \Rightarrow A'(1;1)\)
Vì \(A \in d \Rightarrow A' \in d' \Rightarrow d':\left\{ \begin{array}{l}x = 1 + 4t\\y = 1 + 5t\end{array} \right.\,\,(t \in \mathbb{R})\)
Câu 3: Tìm phương trình đường thẳng d’ là ảnh của đường thẳng d: \(x - 2y + 3 = 0\) qua phép tịnh tiến theo vectơ \(\overrightarrow v = ( - 1;2).\)
Hướng dẫn giải
- Cách 1:
Gọi \(M(x;y) \in d,{T_{\overrightarrow v }}(M) = M'(x';y') \in d'\)
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}x' = x - 1\\y' = y + 2\end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}x = x' + 1\\y = y' - 2\end{array} \right. \Rightarrow M(x' + 1;y' - 2) \in d\\ \Rightarrow x' - 2y' + 8 = 0.\end{array}\)
Vậy phương trình d’ là: \(x - 2y + 8 = 0.\)
- Cách 2:
\({T_{\overrightarrow v }}(d) = d' \Rightarrow d'//d \Rightarrow d':x - 2y + c = 0\)
Chọn
\(M( - 3;0) \in d \\ \Rightarrow {T_{\overrightarrow v }}(M) = M'(x';y')\\ \Rightarrow \left\{ \begin{array}{l}x' = - 3 - 1 = - 4\\y' = 0 + 2 = 0\end{array} \right.\\ \Rightarrow M'( - 4;2).\)
Mà \(M' \in d' \Rightarrow - 4 - 2.2 + c = 0 \Leftrightarrow c = 8 \Rightarrow d':x - 2y + 8 = 0.\)
Câu 4. Cho đường tròn \((C):{(x - 2)^2} + {(y - 1)^2} = 4.\) Tìm ảnh của (C) qua phép tịnh tiến theo vectơ \(\overrightarrow v = \left( { - 2;2} \right).\)
Hướng dẫn giải
- Cách 1:
Đường tròn (C) có tâm I(2;1) bán kính R=2.
Ta có: \({T_{\overrightarrow v }}(C) = C' \Rightarrow {R_{C'}} = R = 2\)
\({T_{\overrightarrow v }}(I) = I' \Rightarrow \left\{ \begin{array}{l}{x_{I'}} = {x_I} + ( - 2) = 0\\{y_{I'}} = {y_I} + 2 = 3\end{array} \right. \Rightarrow I'(0;3)\)
Vậy phương trình (C’) là: \({(x - 0)^2} + {(y - 3)^2} = 4.\)
- Cách 2:
Gọi:
\({T_{\overrightarrow v }}\left( {M(x,y) \in (C)} \right) = M'(x';y') \in (C') \\ \Rightarrow \left\{ \begin{array}{l}x' = x - 1\\y' = y + 2\end{array} \right. \\ \Rightarrow \left\{ \begin{array}{l}x = x' + 2\\y = y' - 2\end{array} \right.\)
\( \Rightarrow M(x' + 2;y' - 2)\)
\(M \in \left( C \right) \Rightarrow x{'^2} + {(y' - 3)^2} = 4 \Rightarrow (C'):{x^2} + {(y - 3)^2} = 4.\)
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Trong mặt phẳng Oxy, tìm ảnh A’, B’ của điểm A(3;-2), B(-1;1) qua phép tịnh tiến theo vectơ \({\rm{\vec u\; = \;}}({\rm{2}};{\rm{3}}).\) Tính độ dài các vectơ \(\overrightarrow {{\rm{AB}}} ,\,\,\,\overrightarrow {{\rm{A'B'}}} .\)
Câu 2: Đường thẳng d cắt Ox tại A(3;0), cắt Oy tại B(0;-4). Viết phương trình tham số của d’ là ảnh của d qua phép tịnh tiến theo vectơ \(\vec v{\rm{\;}} = \left( {1;4} \right).\)
Câu 3: Tìm phương trình đường thẳng d’ là ảnh của đường thẳng d: \(x - 2y - 3 = 0\) qua phép tịnh tiến theo vectơ \(\vec v{\rm{\;}} = ( - 2;3).\)
Câu 4: Cho đường tròn \((C):{(x - 1)^2} + {(y - 2)^2} = 9.\) Tìm ảnh của (C) qua phép tịnh tiến theo vectơ \(\vec v{\rm{\;}} = \left( {1; - 1} \right).\)
Câu 5: Cho \({\mkern 1mu} \Delta :{\mkern 1mu} \,\,3x + y - 1 = 0;{\mkern 1mu} \,\,\,{\Delta _1}:\,\,\,3x + y - 3 = 0.\)
Tìm tọa độ \(\overrightarrow {\rm{w}} \) có phương vuông góc với d để \({d_1} = {T_{\overrightarrow {\rm{W}} }}(d).\)
3.2. Bài tập trắc nghiệm
Câu 1: Tìm mệnh đề đúng trong các mệnh đề sau:
A. Phép tịnh tiến theo vecto v biến M thành M’ thì \(\overrightarrow v = \overrightarrow {MM'} \)
B. Phép tịnh tiến là phép đồng nhất khi vecto tịnh tiến là O→
C. Phép tịnh tiến theo vecto v biến M thành M’ và N thành N’ thì tứ giác MNM’N’ là hình bình hành
D. Phép tịnh tiến theo vecto v biến đường tròn (O;R) thành đường tròn (O;R)
Câu 2: Cho tam giác ABC có trọng tâm G, Gọi D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB. Mệnh đề nào sau đây là sai.
A. \({T_{1/2\overrightarrow {BC} }}\left( F \right) = E\)
B. \({T_{\overrightarrow {DE} }}\left( B \right) = F\)
C. \({T_{2\overrightarrow {DG} }}\left( A \right) = G\)
D. \({T_{1/2\overrightarrow {GA} }}\left( D \right) = G\)
Câu 3: Trong mặt phẳng tọa độ, phép tịnh tiến theo v→(1;2) biến điểm M (-1; 4) thành điểm M’ có tọa độ là:
A. M'(0;6)
B. M’(6;0)
C. M’(0;0)
D. M’(6; 6)
Câu 4: Tìm phương trình đường tròn \(\left( {{C_1}} \right)\) là ảnh của \((C):{(x + 2)^2} + {(y - 1)^2} = 4\) qua phép tịnh tiến theo vectơ \(\overrightarrow v = \left( {2;1} \right).\)
A. \({x^2} + {(y - 1)^2} = 4\)
B. \({x^2} + {(y + 1)^2} = 4\)
C. \({x^2} + {(y - 2)^2} = 4\)
D. \({x^2} + {(y + 2)^2} = 4\)
Câu 5: Hãy tìm vectơ \(\overrightarrow v = \left( {a;b} \right)\) sao cho khi tịnh tiến đồ thị \(y = f(x) = {x^3} + 3x + 1\) theo \(\overrightarrow v \) ta nhận được đồ thị hàm số \(y = g(x) = {x^3} - 3{x^2} + 6x - 1.\)
A. \(\overrightarrow v = \left( {1; - 2} \right)\)
B. \(\overrightarrow v = \left( { - 1;2} \right)\)
C. \(\overrightarrow v = \left( {1;2} \right)\)
D. \(\overrightarrow v = \left( { - 1; - 2} \right)\)
3.3. Trắc nghiệm Online
Các em hãy luyện tập bài trắc nghiệm Phép tịnh tiến Toán 11 sau để nắm rõ thêm kiến thức bài học.
4. Kết luận
Qua bài học này, các em cần nắm được những nội dung sau:
- Khái niệm, tính chất, biểu thức tọa độ và các dạng toán của Phép tịnh tiến.
- Làm được các dạng bài tập liên quan.
Tham khảo thêm
- docx Toán 11 Chương 1 Bài 1: Phép biến hình
- docx Toán 11 Chương 1 Bài 3: Phép đối xứng trục
- docx Toán 11 Chương 1 Bài 4 Phép đối xứng tâm
- docx Toán 11 Chương 1 Bài 5: Phép quay
- docx Toán 11 Chương 1 Bài 6: Khái niệm về phép dời hình và hai hình bằng nhau
- docx Toán 11 Chương 1 Bài 7: Phép vị tự
- docx Toán 11 Chương 1 Bài 8: Phép đồng dạng
.JPG)
