Toán 11 Chương 3 Bài 2: Hai đường thẳng vuông góc
Mời các em cùng tham khảo nội dung bài giảng Hai đường thẳng vuông góc do eLib biên soạn và tổng hợp dưới đây. Bài giảng giúp các em nắm vững lý thuyết bài học, thêm vào đó là những bài tập minh họa có hướng dẫn giải chi tiết sẽ giúp các em dễ dàng làm được các dạng bài tập ở phần này.
Mục lục nội dung

1. Tóm tắt lý thuyết
1.1. Tích vô hướng của hai vectơ trong không gian
a) Góc giữa hai vectơ trong không gian
- Định nghĩa: Trong không gian, cho \(\overrightarrow u \) và \(\overrightarrow v \) là hai vectơ khác vectơ - không. Lấy một điểm A bất kì, gọi B và C là hai điểm sao cho \(\overrightarrow{AB}=\overrightarrow u \), \(\overrightarrow{AC}=\overrightarrow v \). Khi đó ta gọi góc \(\widehat{BAC}\) \(({0^o} \le \widehat {BAC} \le {180^o})\) là góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) trong không gian, kí hiệu là \((\overrightarrow u ,\overrightarrow v)\).
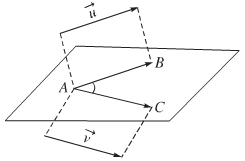
b) Tích vô hướng của hai vectơ trong không gian
- Định nghĩa: Trong không gian cho hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) đều khác vectơ - không. Tích vô hướng của hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) là một số, kí hiệu là \(\vec u .\vec v\), được xác định bởi công thức: \(\overrightarrow u .\overrightarrow v = \left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|.c{\rm{os(}}\overrightarrow {\rm{u}} .\overrightarrow v )\).
- Trường hợp \(\vec u= \vec0\) hoặc \(\vec v= \vec0\) ta quy ước \(\vec u .\vec v = \vec 0\).
1.2. Vectơ chỉ phương của đường thẳng
a) Định nghĩa: Vectơ \(\overrightarrow a \) khác vectơ - không được gọi là vectơ chỉ phương của đường thẳng d nếu giá của vectơ \(\overrightarrow a \) song song hoặc trùng với đường thẳng d.
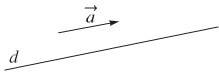
b) Nhận xét:
- Nếu \(\overrightarrow a \) là vectơ chỉ phương của đường thẳng d thì vectơ \(k\overrightarrow a \) với \(\neq 0\) cũng là vectơ chỉ phương của d.
- Một đường thẳng
- Hai đường thẳng song song với nhau khi và chỉ khi chúng là hai đường thẳng phân biệt và có hai vectơ chỉ phương cùng phương.
1.3. Góc giữa hai đường thẳng trong không gian
a) Định nghĩa: Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a' và b' cùng đi qua một điểm và lần lượt song song với a và b.
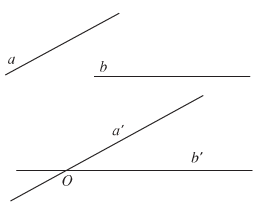
b) Nhận xét:
- Để xác định góc giữa hai đường thẳng a và b ta có thể lấy điểm O thuộc một trong hai đường thẳng đó rồi vẽ đường thẳng qua O và song song với đường thẳng còn lại.
- Nếu \(\overrightarrow u \) là vectơ chỉ phương của đường thẳng a và \(\overrightarrow v \) là vectơ chỉ phương của đường thẳng b và \(\left ( \overrightarrow{u},\overrightarrow{v} \right )=\alpha\) thì góc giữa hai đường thẳng a và b bằng \(\alpha\) nếu \(0^o\leq \alpha \leq 90^o\) và bằng \(180^o-\alpha\) nếu \(90^o\leq \alpha \leq 180^o\). Nếu a và b song song với nhau thì góc giữa chúng bằng \(0^o\).
1.4. Hai đường thẳng vuông góc
a) Định nghĩa: Hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng \(90^o\).
b) Nhận xét:
- Nếu \(\overrightarrow u \) và \(\overrightarrow v \) lần lượt là các vectơ chỉ phương của đường thẳng a và b thì: \(a\perp b\Leftrightarrow \overrightarrow{u}.\overrightarrow{v}=0\).
- Cho hai đường thẳng song song. Nếu một đường thẳng vuông góc với một trong hai đường thẳng này thì vuông góc với đường thẳng kia.
- Hai đường thẳng vuông góc với nhau có thể cắt nhau hoặc chéo nhau.
2. Bài tập minh họa
Bài 1: Cho tứ diện đều ABCD có H là trung điểm cạnh AB. Hãy tính góc giữa các cặp vectơ sau:
a) \(\overrightarrow {AB} \) và \(\overrightarrow {BD} \).
b) \(\overrightarrow {DH} \) và \(\overrightarrow {AD} \).
Hướng dẫn giải:
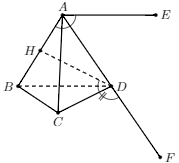
a) Dựng \(\overrightarrow {AE} =\overrightarrow {BD} \).
Ta có \((\overrightarrow {AB}, \overrightarrow {BD})=(\overrightarrow {AB}, \overrightarrow {AE})=\widehat{BAE}=120^o\).
b) Dựng \(\overrightarrow {DF} =\overrightarrow {AD} \).
Ta có \((\overrightarrow {DH}, \overrightarrow {AD})=(\overrightarrow {DH}, \overrightarrow {DF})=\widehat{HDF}=180^o-30^o=120^o\).
Bài 2: Cho tứ diện ABCD có AB = CD = a, \(IJ = \frac{{a\sqrt 3 }}{2}\) (I thuộc BC, J thuộc AD). Tính \(\widehat{(AB,CD})\).
Hướng dẫn giải:
.png)
Gọi M, N lần lượt là trung điểm của AC, BC.
Ta có:
\(\left\{ \begin{array}{l} MI = NI = \frac{1}{2}AB = \frac{1}{2}CD = \frac{a}{2}\\ MI//AB//CD//NI \end{array} \right.\)
Suy ra MINJ là hình thoi.
Gọi O là tâm của hình thoi MINJ.
Ta có \(\widehat {MIN} = 2\widehat {MIO}\).
Xét tam giác MIO vuông tại O có:
\(\cos MIO = \frac{{IO}}{{MI}} = \frac{{\frac{{a\sqrt 3 }}{4}}}{{\frac{a}{2}}} = \frac{{\sqrt 3 }}{2}\)
Suy ra \(\widehat {MIO} =30^o\) \(\Rightarrow \) \(\widehat {MIN} =60^o\).
Vậy (AB,CD) = (IM,IN) = \(60^o\).
Bài 3: Cho tứ diện ABCD, hai tam giác ABC và ABD là hai tam giác đều.
a) Chứng minh \(AB \bot CD\).
b) Gọi M, N, P, Q lần lượt là trung điểm của AC, BC, BD, DA. Chứng minh rằng tứ giác MNPQ là hình chữ nhật.
Hướng dẫn giải:
.png)
a) Ta có:
\(\overrightarrow {CD} .\overrightarrow {AB} = \left( {\overrightarrow {AD} - \overrightarrow {AC} } \right)\overrightarrow {AB} = \overrightarrow {AD} \overrightarrow {AB} - \overrightarrow {AC} \overrightarrow {AB} \).
Đặt AB = a ta có AD = AB = AC = a.
Do đó
\(\begin{array}{l} \overrightarrow {CD} .\overrightarrow {AB} = \left| {\overrightarrow {AD} } \right|.\left| {\overrightarrow {AB} } \right|.cos{60^o} - \left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {AB} } \right|cos{60^o}\\ = a.a.\frac{1}{2} - a.a.\frac{1}{2} = 0 \end{array}\)
Vậy \(AB \bot CD\).
b) Ta có MN // PQ // AB và MN = PQ = \(\frac{1}{2}AB\).
Suy ra tứ giác MNPQ là hình bình hành.
Vì MN // AB và NP // CD mà \(AB \bot CD\). Nên tứ giác MNPQ là hình chữ nhật.
3. Luyện tập
3.1. Bài tập tự luận
Bài 1: Cho hình chóp S.ABCD có tất cả các cạnh đều bằng nhau, đáy là hình vuông. Gọi N là trung điểm SB.
a) Chứng minh rằng tam giác SAC và tam giác SBD là các tam giác vuông.
b) Tính góc giữa hai đường thẳng AN và CN; AN và SD.
Bài 2: Cho hình chóp S.ABCD có đáy là hình thoi, tam giác SAC cân tại S, M và N là trung điểm của AD và CD, P là điểm thuộc cạnh SB sao cho BP = 3 PS.
a) Tính góc giữa hai đường thẳng AC và SD.
b) Xác định thiết diện của hình chóp với (MNP).
Bài 3: Cho tứ diện đều ABCD. Gọi I, J lần lượt là trung điểm của AB, CD. Chứng minh rằng:
a) IJ vuông góc với AB.
b) IJ vuông góc với CD.
c) AB vuông góc với CD.
Bài 4: Cho tứ diện ABCD có BA = CA = DA, \(\widehat{BAC}=\widehat{BAD}=60^o\), MA = MB, NC = ND. Chứng minh MN là đường vuông góc chung của các đường thẳng AB và CD.
3.2. Bài tập trắc nghiệm
Bài 1: Cho tứ diện đều MNPQ. Tính số đo giữa hai đường thẳng MN và PQ.
A. \(60^o\).
B. \(30^o\).
C. \(90^o\).
D. \(45^o\).
Bài 2: Cho hình lập phương ABCD. A'B'C'D'. Khẳng định nào sau đây là không đúng?
A. Góc giữa AC và B'D' bằng \(90^o\).
B. Góc giữa B'D' và AA' bằng \(60^o\).
C. Góc giữa AD và B'C bằng \(45^o\).
D. Góc giữa BD và A'C' bằng \(90^o\).
Bài 3: Cho tứ diện ABCD có BD vuông góc AB và CD. Gọi P và Q lần lượt là trung điểm của các cạnh CD và AB thỏa mãn \(BD:CD:PQ:AB=3:4:5:6\). Gọi \(\alpha\) là góc giữa hai đường thẳng AB và CD. Giá trị của cos\(\alpha\):
A. \(\frac{7}{8}\).
B. \(\frac{1}{2}\).
C. \(\frac{11}{16}\).
D. \(\frac{1}{4}\).
Bài 4: Cho hình chóp S.ABC có hai tam giác cân là tam giác SAB và tam giác ABC. Tính số đo của góc giữa hai đường thẳng chéo nhau SC và AB.
A. \(30^o\).
B. \(45^o\).
C. \(60^o\).
D. \(90^o\).
Bài 5: Cho hình chóp S.ABC. Tam giác ABC là tam giác đều. Lấy M, N, P lần lượt là trung điểm của các cạnh BC, SB và SC. Đường thẳng AM vuông góc với đường thẳng nào sau đây?
A. NP.
B. BN.
C. CN.
D. CP.
3.3. Trắc nghiệm Online
4. Kết luận
Qua bài học này các em cần nắm các nội dung sau:
- Khái niệm vectơ chỉ phương của đường thẳng; khái niệm góc giữa hai đường thẳng; khái niệm và điều kiện hai đường thẳng vuông góc với nhau.
- Làm được các dạng toán: xác định vectơ chỉ phương của đường thẳng; góc giữa hai đường thẳng; chứng minh ai đường thẳng vuông góc với nhau.
Tham khảo thêm
- doc Toán 11 Chương 3 Bài 1: Vectơ trong không gian
- doc Toán 11 Chương 3 Bài 3: Đường thẳng vuông góc với mặt phẳng
- doc Toán 11 Chương 3 Bài 4: Hai mặt phẳng vuông góc
- doc Toán 11 Chương 3 Bài 5: Khoảng cách
- doc Toán 11 Ôn tập chương 3: Vectơ trong không gian. Quan hệ vuông góc trong không gian
