Toán 11 Chương 1 Bài 1: Hàm số lượng giác

a) Hàm số sin

Xét hàm số \(y = \sin x\)

- Tập xác định: \(D=\mathbb{R}.\)

- Tập giá trị: \([-1;1].\)

- Hàm số tuần hòa với chu kì \(2\pi \).

- Sự biến thiên:

• Hàm số đồng biến trên mỗi khoảng \(\left( {-\frac{{ \pi }}{2} + k2\pi ;\,\,\frac{\pi }{2} + k2\pi } \right)\), \(k \in \mathbb{Z}.\)
• Hàm số nghịch biến trên mỗi khoảng \(\left( {k2\pi ;\,\,\pi + k2\pi } \right)\), \(k \in \mathbb{Z}\).

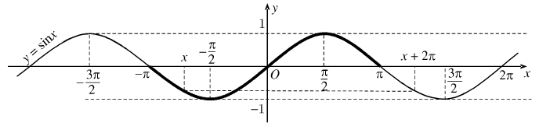
- Đồ thị hàm số \(y = \sin x\)

• Đồ thị là một đường hình sin.
• Do hàm số \(y = \sin x\) là hàm số lẻ nên đồ thị nhận gốc tọa độ làm tâm đối xứng.
• Đồ thị hàm số \(y = \sin x\):

​

b) Hàm số cosin

Xét hàm số \(y = \cos x\)

- Tập xác định: \(\mathbb{R}\)

- Tập giá trị: \([-1;1].\)

- Hàm số tuần hòa với chu kì: \(2\pi \)

- Sự biến thiên:

• Hàm số đồng biến trên mỗi khoảng \(( - \pi + k2\pi ;\,\,k2\pi )\), \(k \in \mathbb{Z}\).
• Hàm số nghịch biến trên mỗi khoảng \((k2\pi ;\,\,\pi + k2\pi )\), \(k \in \mathbb{Z}\).

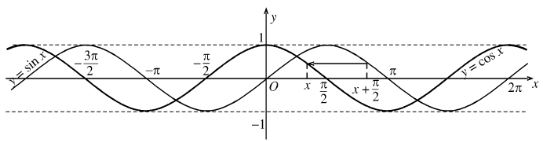
- Đồ thị hàm số \(y = \cos x\)

• Đồ thị hàm số là một đường hình sin.
• Hàm số \(y = \cos x\) là hàm số chẵn nên đồ thị nhận trục tung làm trục đối xứng.
• Đồ thị hàm số \(y = \cos x\)​:

a) Hàm số \(y = \tan x\)

- Tập xác định \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,\left( {k \in \mathbb{Z}} \right)} \right\}.\) 

- Hàm số tuần hoàn với chu kì \(\pi.\) 

- Tập giá trị là \(\mathbb{R}\).

- Hàm số đồng biến trên mỗi khoảng \(\left( {\frac{{ - \pi }}{2} + k\pi ;\,\frac{\pi }{2} + \,k\pi } \right),\,\,k \in \mathbb{Z}.\)

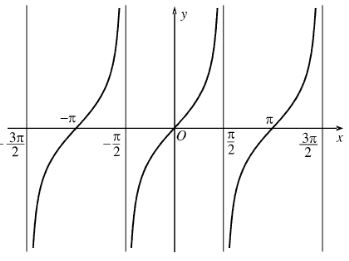
- Đồ thị hàm số \(y = \tan x\)​

• Hàm số \(y = \tan x\) là hàm số lẻ nên đồ thị nhận gốc tọa độ O làm tâm đối xứng.
• Đồ thị hàm số \(y = \tan x\):

b) Hàm số \(y = \cot x\)

- Tập xác định \(\mathbb{R}\backslash \left\{ {k\pi ,\left( {k \in } \right)} \right\}.\) 

- Tập giá trị là \(\mathbb{R}.\)

- Hàm số tuần hoàn với chu kì \(\pi .\) 

- Hàm số nghịch biến trên mỗi khoảng  \(\left( {k\pi ;\,\pi + \,k\pi } \right),\,\,k \in \mathbb{Z}.\)

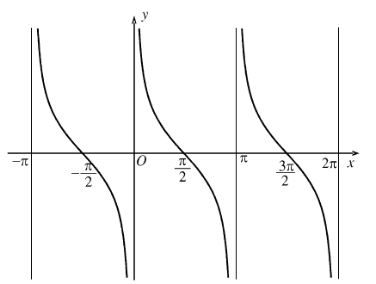
- Đồ thị hàm số \(y = \cot x\)

• Hàm số \(y = \cot x\) là hàm số lẻ nên đồ thị nhận gốc tọa độ làm tâm đối xứng.
• Đồ thị hàm số \(y = \cot x\)​:

Câu 1: Tìm tập xác định các hàm số sau:

a) \(y = \frac{{1 + \sin x}}{{\cos x}}\)

b) \(y = \tan \left( {x + \frac{\pi }{4}} \right)\)

c) \(y = \cot \left( {\frac{\pi }{3} - 2x} \right)\)

Hướng dẫn giải

a) Hàm số \(y = \frac{{1 + \sin x}}{{\cos x}}\) xác định khi \(cosx\ne0\) hay \(x \ne \frac{\pi }{2} + k\pi \,(k \in\mathbb{Z} ).\)

b) Hàm số \(y = \tan \left( {x + \frac{\pi }{4}} \right)\) xác định khi \(x + \frac{\pi }{4} \ne \frac{\pi }{2} + k\pi \Leftrightarrow x \ne \frac{\pi }{4} + k\pi \,(k \in\mathbb{Z} ).\)

c) Hàm số \(y = \cot \left( {\frac{\pi }{3} - 2x} \right)\) xác định khi \(\frac{\pi }{3} - 2x \ne k\pi \Leftrightarrow x \ne \frac{\pi }{6} - k\frac{\pi }{2}\left( {k \in\mathbb{Z} } \right).\)

Câu 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:

a) \(y = 3\sin \left( {x - \frac{\pi }{6}} \right) + 1\)

b) \(y=\sqrt{1+\cos2x}-5\)

Hướng dẫn giải

a) Ta có: \(- 1 \le \sin \left( {x - \frac{\pi }{6}} \right) \le 1 \)

\(\Rightarrow - 3 \le 3\sin \left( {x - \frac{\pi }{6}} \right) \le 3\)

\(\Rightarrow - 2 \le 3\sin \left( {x - \frac{\pi }{6}} \right) + 1 \le 4\)

Vậy giá trị lớn nhất của hàm số là 4, giá trị nhỏ nhất cả hàm số là -2.

b) Ta có: \(- 1 \le \cos 2x \le 1 \)

\(\Rightarrow 0 \le 1 + \cos 2x \le 2\)

\(\Rightarrow 0 \le \sqrt {1 + \cos 2x} \le \sqrt 2 \)

\(\Rightarrow - 5 \le \sqrt {1 + \cos 2x} - 5 \le \sqrt 2 - 5\)

Vậy giá trị lớn nhất của hàm số là \(\sqrt2-5\), giá trị nhỏ nhất của hàm số là -5.

Câu 3: Tìm chu kì tuần hoàn của các hàm số lượng giác sau:

a) \(y = \frac{3}{2} + \frac{1}{2}\cos 2x\)

b) \(y = 2\cos 2x\)

c) \(y = \tan \left( {2x + \frac{\pi }{4}} \right)\)

Hướng dẫn giải

a) Hàm số \(y = \frac{3}{2} + \frac{1}{2}\cos 2x\) có chu kì tuần hoàn là \(T = \frac{{2\pi }}{{\left| 2 \right|}} = \pi .\)

b) Hàm số \(y = 2\cos 2x\) có chu kì tuần hoàn là \(T = \frac{{2\pi }}{{\left| 2 \right|}} = \pi .\)

c) Hàm số \(y = \tan \left( {2x + \frac{\pi }{4}} \right)\) có chu kì tuần hoàn là \(T = \frac{{\pi }}{{\left| 2 \right|}} = \frac{\pi}{2} .\)

Câu 1. Tìm tập xác định của hàm số \(y = \cot x\)

A. \(R\backslash \left\{ {\frac{\pi }{4} + k\pi ,k \in Z} \right\}\)

B. \(R\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in Z} \right\}\)

C. \(R\backslash \left\{ {k\frac{\pi }{2},k \in Z} \right\}\)

D. \(R\backslash \left\{ {k\pi ,k \in Z} \right\}\)

Câu 2. Tập xác định của hàm số \(y = \tan x\)

A. R

B. \(R\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in Z} \right\}\)

C. \(R\backslash \left\{ {k\pi ,k \in Z} \right\}\)

D. \(R\backslash \left\{ {k\frac{\pi }{2},k \in Z} \right\}\)

Câu 3. Giá trị nhỏ nhất và giá trị lớn nhất của hàm số lần lượt là: 

A. -8 và -2 

B. 2 và 8

C. -5 và 2

D. -5 và 3 

Câu 4. Tìm giá trị lớn nhất M của hàm số \(y = {\sin ^4}x + {\cos ^4}x.\)

A. M=0

B. M=1

C. M=2

D. \(M = \frac{1}{2}\)

Câu 5. Tìm tập giá trị của hàm số \(y = 1 - 2\left| {\sin 3x} \right|.\)

A. \({\rm{[}} - 1;1]\)

B. \(\left[ {0;1} \right]\)

C. \(\left[ { - 1;0} \right]\)

D. \(\left[ { - 1;3} \right]\)

Qua bài học này, các em cần nắm được những nội dung sau:

• Nắm được hình dạng của hàm số sin, hàm số cos, hàm số tan và hàm số cot.
• Làm được các bài tập liên quan.