Toán 11 Chương 2 Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song
eLib đã biên soạn và tổng hợp để giới thiệu đến các em nội dung bài Hai đường thẳng chéo nhau và hai đường thẳng song song. Bài giảng giúp các em biết cách xác định vị trí tương đối của hai đường thẳng trong không gian, kèm theo đó là những bài tập minh họa có hướng dẫn giải chi tiết giúp các em hiểu bài hơn. Mời các em cùng tham khảo.
Mục lục nội dung

1. Tóm tắt lí thuyết
1.1. Vị trí tương đối của hai đường thẳng trong không gian
Cho hai đường thẳng a và b trong không gian. Khi đó có các trường hợp xảy ra với a và b.
- Trường hợp 1: Có một mặt phẳng chứa a và b (ta nói a và b đồng phẳng)
+ a và b có điểm chung duy nhất M. Ta nói a và b cắt nhau tại M và kí hiệu \(a \cap b=M\).
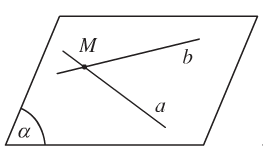
+ a và b không có điểm chung. Ta nói a và b song song với nhau và kí hiệu là a // b.
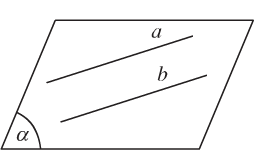
+ a trùng b, kí hiệu \(a \equiv b\).
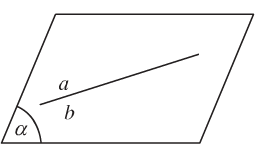
- Trường hợp 2: Không có mặt phẳng nào chứa a và b.
Khi đó ta nói a và b chéo nhau hay a chéo với b.
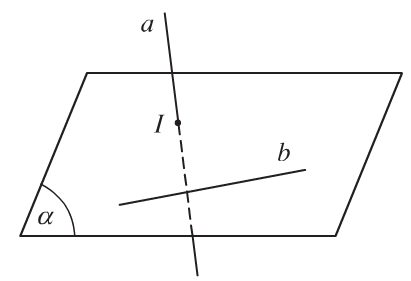
1.2. Tính chất
- Định lí 1: Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có một và chỉ một đường thẳng song song với đường thẳng đã cho.
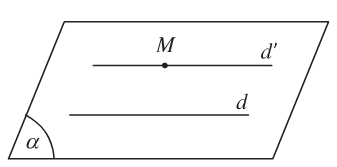
+ Nhận xét: Hai đường thẳng song song a và b xác định một mặt phẳng, kí hiệu là mp(a,b) hay (a,b).
- Định lí 2: Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song với nhau.
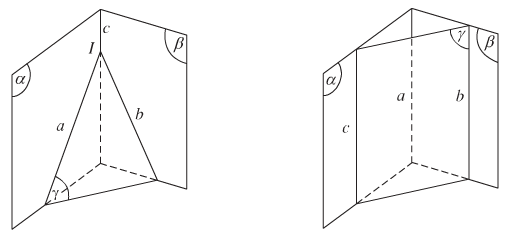
- Hệ quả: Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
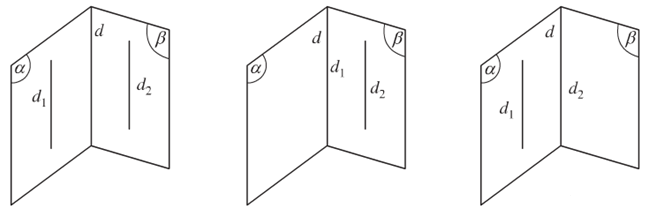
- Định lí 3: Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.
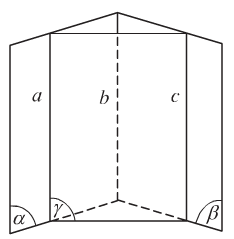
2. Bài tập minh họa
Bài 1: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I, J lần lượt là trung điểm của các cạnh AD và BC và G là trọng tâm của tam giác SCD. Tìm giao tuyến của hai mặt phẳng (SCD) và (IJG).
Hướng dẫn giải:
.png)
Ta có ABCD là hình bình hành và I, J là trung điểm của AD và BC nên IJ // AB.
Có
\(\left\{ \begin{array}{l} G \in \left( {SAB} \right) \cap \left( {IJG} \right)\\ AB \subset \left( {SAB} \right)\\ IJ \subset \left( {IJG} \right)\\ IJ//AB \end{array} \right. \Rightarrow \left( {SAB} \right) \cap \left( {IJG} \right) = MN\) với MN đi qua G và song song với AB.
Bài 2: Cho hình chóp S.ABCD có đáy ABCD là một hình thang với đáy bé CD. Gọi M, N lần lượt là trung điểm của SA và SB.
a) Chứng minh MN // CD.
b) Gọi P là giao điểm của SC và (AND), I là giao điểm của AN và DP. Chứng minh SI // CD.
Hướng dẫn giải:
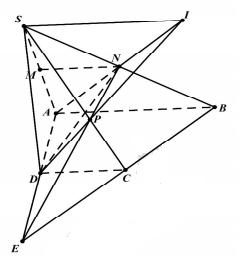
a) Ta có: M, N là trung điểm của SA và SB \(\Rightarrow \) MN là đường trung bình của tam giác SAB nên MN // AB (1).
Lại có AB // CD (ABCD là hình bình hành) (2).
Từ (1) và (2) suy ra MN // CD.
b) Trong (ABCD) gọi \(E=AD \cap BC\).
Trong (SCD) gọi \(P=SC \cap EN\).
Ta có: E \(\in\) AD \( \subset \) (AND).
\(\Rightarrow \)EN \( \subset \) (AND) \(\Rightarrow \)P \(\in\) (AND).
Vậy P = SC \(\cap \) (AND).
Lại có I là giao điểm của AN và DP.
\( \Rightarrow \left\{ \begin{array}{l} I \in AN\\ I \in DP \end{array} \right. \Rightarrow \left\{ \begin{array}{l} I \in \left( {SAB} \right)\\ I \in \left( {SCD} \right) \end{array} \right. \Rightarrow SI = \left( {SAB} \right) \cap \left( {SCD} \right)\).
Vì \(\left\{ \begin{array}{l} \left( {SAB} \right) \cap \left( {SCD} \right) = SI\\ AB \subset \left( {SAB} \right)\\ CD \subset \left( {SCD} \right)\\ AB//CD \end{array} \right. \Rightarrow \)SI // CD.
Bài 3: Cho hình chóp S.ABCD có đáy ABCD là một tứ giác lồi. Gọi M, N, E, F lần lượt là trung điểm của các cạnh bên SA, SB, SC và SD.
a) Chứng minh ME, NF, SO đồng qui (O là giao điểm của AC và BD).
b) Bốn điểm M, N, E, F đồng phẳng.
Hướng dẫn giải:
.png)
a) Trong (SAC) gọi I = ME \(\cap \) SO \(\Rightarrow \) I là trung điểm của SO \(\Rightarrow \) FI là đường trung bình của tam giác SOD.
Do đó FI // OD.
Tương tự ta có NI // OB nên N, I, F thẳng hàng hay I \( \subset \) NF.
Vậy ME, NF, SO đồng qui.
b) Do ME \(\cap \) NF = I nên ME và NF xác định một mặt phẳng. Suy ra M, N, E, F đồng phẳng.
3. Luyện tập
3.1. Bài tập tự luận
Bài 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC).
b) Gọi M là một điểm trên cạnh SC. Xác định giao điểm N của SD với (ABM). Tứ giác ABMN là hình gì?
Bài 2: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh SA, SB, SC, SD.
a) Chứng minh MNPQ là hình bình hành.
b) Gọi I là một điểm trên cạnh BC. Xác định thiết diện của hình chóp với (IMN).
Bài 3: Cho tứ diện đều ABCD cạnh a. Gọi M, N lần lượt là trung điểm của CD và AB.
a) Hãy xác định các điểm I \(\in\) AC và J \(\in\) DN sao cho IJ // BM.
b) Tính IJ theo a.
3.2. Bài tập trắc nghiệm
Bài 1: Cho hình chóp S.ABCD có đáy là hình thang với các cạnh đáy là AB và CD. Gọi M, N lần lượt là trung điểm của SA, SB. Khẳng định nào sau đây là đúng?
A. MN // CD.
B. MN, CD chéo nhau.
C. MN cắt CD.
D. MN \( \equiv \) CD.
Bài 2: Cho hình chóp S.ABCD có AD không song song với BC. Gọi M, N, P, Q, R, T lần lượt là trung điểm của AC, BD, BC, CD, SA, SD. Cặp đường thẳng nào sao đây song song với nhau?
A. MP và RT.
B. MQ và RT.
C. MN và RT.
D. PQ và RT.
Bài 3: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi K là trung điểm SA. Thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (KBC) là:
A. Tam giác KBC.
B. Hình thang KBCH (H là trung điểm SD).
C. Hình thang KGBC (G là trung điểm SB).
D. Tứ giác KBCD.
Bài 4: Cho tứ diện ABCD, M và N lần lượt là trung điểm AB và AC. Mặt phẳng \(\left( \alpha \right)\) qua MN cắt tứ diện ABCD theo thiết diện là đa giác T. Khẳng định nào sau đây là đúng?
A. T là hình chữ nhật.
B. T là tam giác.
C. T là hình thoi.
D. T là tam giác hoặc hình thang hoặc hình bình hành.
Bài 5: Cho tứ diện ABCD. Các điểm P, Q lần lượt là trung điểm của AB và CD; điểm R nằm trên cạnh BC sao cho BR = 2RC. Gọi S là giao điểm của mặt phẳng (PQR) và cạnh AD. Tính tỉ số ?
A. 2.
B. 1.
C. \(\frac{1}{2}\).
D. \(\frac{1}{3}\).
3.3. Trắc nghiệm Online
Các em hãy luyện tập bài trắc nghiệm Hai đường thẳng chéo nhau và hai đường thẳng song song Toán 11 sau để nắm rõ thêm kiến thức bài học.
4. Kết luận
Qua bài học này các em cần nắm được các nội dung sau:
- Khái niệm hai đường thẳng: trùng nhau, song song, cắt nhau, chéo nhau trong không gian và các định lí, hệ quả trong bài học.
- Biết cách áp dụng các định lí để giải bài tập.
Tham khảo thêm
- doc Toán 11 Chương 2 Bài 1: Đại cương về đường thẳng và mặt phẳng
- doc Toán 11 Chương 2 Bài 3: Đường thẳng và mặt phẳng song song
- doc Toán 11 Chương 2 Bài 4: Hai mặt phẳng song song
- doc Toán 11 Chương 2 Bài 5: Phép chiếu song song. Hình biểu diễn của một hình không gian
- doc Toán 11 Ôn tập chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
