Toán 11 Chương 1 Bài 6: Khái niệm về phép dời hình và hai hình bằng nhau

a) Định nghĩa: Phép dời hình là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kỳ.

Ký hiệu: F

- Nếu F(M) = M’ và F(N) = N’ thì MN = M’N’

b) Nhận xét

- Các phép đồng nhất, tịnh tiến, đối xứng trục, đối xứng tâm, quay đều là phép dời hình.

- Phép biến hình có được bằng cách thực hiện liên tiếp hai phép dời hình cũng là một phép dời hình.

• Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm.

• Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng bằng nó.

• Biến tam giác thành tam giác bằng nó, biến góc thành góc bằng nó.

• Biến đường tròn thành đường tròn có cùng bán kính.

Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.

Câu 1: 

a) Cho hình vuông ABCD tâm O. Tìm ảnh của các điểm A, B, O qua phép dời hình có được bằng cách thực hiện liên tiếp hai phép \({Q_{\left( {O{{,90}^0}} \right)}}\) và phép ĐBD.

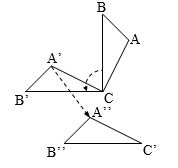
b) Quan sát hình vẽ và cho biết \(\Delta ABC\) biến thành \(\Delta A''B''C''\) qua phép dời hình nào?

Hướng dẫn giải

a) Ta có:

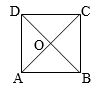
\(\left\{ \begin{array}{l}{Q_{\left( {O{{,90}^0}} \right)}}\left( O \right) = O\\{Q_{\left( {O{{,90}^0}} \right)}}\left( A \right) = B\\{Q_{\left( {O;{{90}^0}} \right)}}\left( B \right) = C\end{array} \right.\) và ĐBD(O)=O; ĐBD(B)=B; ĐBD(C)=A.

Vậy ảnh của O là O, A là B và B là A.

b) Ta có:

\({Q_{\left( {C{{,90}^0}} \right)}}\left( {ABC} \right) = A'B'C\)

\({T_{\overrightarrow {AA''} }}\left( {A'B'C} \right) = A''B''C''.\)

Vậy phép dời hình cần tìm là phép biến hình thực hiện liên tiếp hai phép\({Q_{\left( {C{{,90}^0}} \right)}}\) và \({T_{\overrightarrow {AA''} }}.\)

Câu 2: Cho lục giác đều ABCDEF tâm O. Hãy xác định ảnh của \(\Delta OAB\)qua phép dời hình bằng cách thực hiện liên tiếp phép quay tâm O, góc quay 60⁰ và phép tịnh tiến theo vectơ \(\overrightarrow {OE} .\)

Hướng dẫn giải

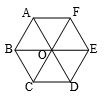
Ta có:

\(\left\{ \begin{array}{l}{Q_{\left( {O{{,60}^0}} \right)}}\left( A \right) = B\\{Q_{\left( {O{{,60}^0}} \right)}}\left( B \right) = C\end{array} \right.\)\( \Rightarrow {Q_{\left( {O{{,60}^0}} \right)}}\left( {OAB} \right) = OBC\)

\(\left\{ \begin{array}{l}{T_{\overrightarrow {OE} }}\left( O \right) = E\\{T_{\overrightarrow {OE} }}\left( B \right) = O\\{T_{\overrightarrow {OE} }}\left( C \right) = D\end{array} \right. \Rightarrow {T_{\overrightarrow {OE} }}\left( {OBC} \right) = EOD\)

Vậy ảnh của \(\Delta OAB\)qua phép dời hình đã cho là \(\Delta EOD\).

Câu 3: Cho hình chữ nhật ABCD tâm O. Gọi E, F lần lượt là trung điểm của AD và BC. Chứng minh rằng hình thang AEOB và hình thang CFOD bằng nhau.

Hướng dẫn giải

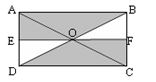
Ta có:

Đo(O)=O; ĐO(A)=C; ĐO(E)=F; ĐO(B)=D.

Suy ra: ĐO(AEOB)=CFOD.

Vậy có phép dời hình là phép đối xứng tâm O biến hình thang AEOB thành hình thang CFOD. Vậy hai hình thang này bằng nhau.

Câu 1: Cho chữ nhật ABCD tâm O. Tìm ảnh của các điểm A, B, O qua phép dời hình có được bằng cách thực hiện liên tiếp hai phép \({Q_{\left( {O,{{90}^0}} \right)}}\) và phép Đ_BD.

Câu 2: Cho lục giác đều ABCDEF tâm O. Hãy xác định ảnh của \(\Delta OCD\) qua phép dời hình bằng cách thực hiện liên tiếp phép quay tâm O, góc quay 60⁰ và phép tịnh tiến theo vectơ \(\overrightarrow {OA} .\)

Câu 3: Cho hình hình hành ABCD tâm O. Gọi E, F lần lượt là trung điểm của AB và CD. Chứng minh rằng hình thang ABFD và hình thang CDEB bằng nhau.

Câu 1: Cho hình chữ nhật ABCD như hình vẽ, phép biến hình biến hình (1) thành hình (3) là thực hiện liên tiếp hai phép dời hình nào sau đây.

A.  Phép đối xứng tâm I và phép đối xứng trục IB.

B. Phép đối xứng tâm I và phép quay tâm I góc quay 900.

C. Phép đối xứng trục EI và phép tịnh tiến theo \(\overrightarrow {DI} \).

D. Phép tịnh tiến theo \(\overrightarrow {AI} \) và phép đối xứng tâm I.

Câu 2: Cho hình vuông ABCD như hình vẽ, tam giác BIG là ảnh của tam giác DIH qua:

A. Phép đối xứng tâm I

B. Phép quay tâm I góc quay 900

C. Phép tịnh tiến theo \(\overrightarrow {DI} \)

D. Phép quay tâm A góc quay 900

Câu 3: Trong mặt phẳng Oxy, thực hiện liên tiếp phép đối xứng tâm O và phép quay tâm O góc quay 900 biến đường thẳng y = x + 1 thành đường thẳng

A. x-y-1=0

B. -x+y-1=0

C. x+y+1=0

D. x+y-1=0

Câu 4: Cho hai điểm A, B phân biệt. Gọi ĐA, ĐB là các phép đối xứng qua A, B. Với điểm M bất kì, gọi M1=ĐA(M), M2=ĐB(M1). Gọi F là phép biến hình biến M thành M2. Chọn khẳng định đúng.

A. F là phép quay.

B. F là phép đối xứng trục.

C. F là phép đối xứng tâm.

D. F là phép tịnh tiến.

Câu 5: Cho hình chữ nhật ABCD. Gọi E, F, H, K, O, I, J lần lượt là trung điểm của các cạnh AB, BC, CD, DA, KF, HC, KO. Khẳng định nào sau đây đúng?

A. Phép quay tâm O góc quay \({90^0}\) biến tam giác OKA thành tam giác OCF.

B. Tồn tại phép dời hình  bằng cách thực hiện liên tiếp phép đối xứng trục và phép tịnh tiến biến hình thang AEJK thành hình thang FOIC.

C. Phép dời hình gồm phép tịnh tiến theo vectơ \(\overrightarrow {HD} \) và phép đối xứng trục KF biến hình thang FIOC thành hình thang AEJK.

D. Không tồn tại phép quay tâm O nào biến tam giác OKA thành tam giác OCF.

Qua bài học này, các em cần nắm được những nội dung sau:

• Thấy được các điểm chung, mối liên hệ của các phép tịnh tiến, phép đối xứng tâm, phép đối xứng trục, phép quay
• Nắm được phương pháp giải bài tập.