Toán 11 Chương 2 Bài 3: Đường thẳng và mặt phẳng song song

Cho đường thẳng d và mặt phẳng \(\left( \alpha \right)\). Ta có các trường hợp sau:

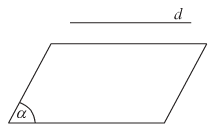
- d và \(\left( \alpha \right)\) không có điểm chung. Ta nói d song song với \(\left( \alpha \right)\) hay \(\left( \alpha \right)\) song song với d, kí hiệu là d // \(\left( \alpha \right)\) hay \(\left( \alpha \right)\) // d.

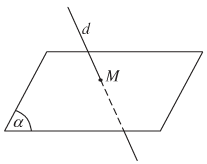
- d và \(\left( \alpha \right)\) có một điểm chung duy nhất M. Ta nói d và \(\left( \alpha \right)\) cắt nhau, kí hiệu là d \(\cap \) \(\left( \alpha \right)\) = M.

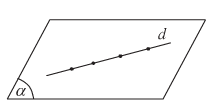
- d và \(\left( \alpha \right)\) có từ hai điểm chung trở lên. Ta nói d nằm trong \(\left( \alpha \right)\) hay \(\left( \alpha \right)\) chứa d, kí hiệu là  \(d\subset \left( \alpha \right)\) hay \(\left( \alpha \right) \supset d\) .

- Định lí 1: Nếu đường thẳng d không nằm trong mặt phẳng \(\left( \alpha \right)\) và d song song với đường thẳng d’ nằm trong \(\left( \alpha \right)\) thì d song song với \(\left( \alpha \right)\).

\(\left\{ \begin{array}{l} d \not\subset \left( \alpha \right)\\ d' \subset \left( \alpha \right)\\ d//d' \end{array} \right. \Rightarrow \)d // \(\left( \alpha \right)\).

- Định lí 2: Cho đường thẳng a song song với mặt phẳng \(\left( \alpha \right)\) . Nếu mặt phẳng \(\left( \beta \right)\) chứa a và cắt \(\left( \alpha \right)\) theo giao tuyến b thì b song song với a.

\(\left\{ \begin{array}{l} a//\left( \alpha \right)\\ a \subset \left( \beta \right)\\ \left( \alpha \right) \cap \left( \beta \right) = b \end{array} \right. \Rightarrow \)b // a

- Hệ quả: Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.

 \(\left\{ \begin{array}{l} d//\left( \alpha \right)\\ d//\left( \beta \right)\\ \left( \alpha \right) \cap \left( \beta \right) = d' \end{array} \right. \Rightarrow \)d // d’

- Định lí 3: Cho hai đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.

Bài 1: Cho tứ diện ABCD. G là trọng tâm của tam giác ABC. Trên cạnh BD lấy điểm K sao cho KB = 2 KD. Chứng minh rằng KG // (ACD).

Hướng dẫn giải:

Gọi I là trung điểm của AC.

Ta có KB = 2KD \(\Rightarrow \frac{{KB}}{{BD}} = \frac{2}{3}\) .

Lại có \(\frac{{BG}}{{BI}} = \frac{2}{3}\) (G là trọng tâm tam giác ABC).

Suy ra \(\frac{{KB}}{{BD}} = \frac{{BG}}{{BI}}\).

Nên KG // DI (định lí Ta – lét đảo).

Mà DI \( \subset \) (ACD).

Vậy KG // (ACD).

Bài 2: Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD, O là giao điểm hai đường chéo, M là trung điểm của SA. Mặt phẳng (P) qua M và song song với SC và AD. Tìm thiết diện của mặt phẳng (P) với hình chóp S.ABCD.

Hướng dẫn giải:

Ta có:

+ \(\left\{ \begin{array}{l} M \in \left( \alpha \right) \cap \left( {SAD} \right) \\ \left( \alpha \right)//AD\\ AD \subset \left( {SAD} \right) \end{array} \right. \Rightarrow \left( \alpha \right) \cap \left( {SAD} \right) = MN//AD\)  \(\left( {N \in SD} \right)\).

+ \(\left\{ \begin{array}{l} N \in\left( \alpha \right) \cap \left( {SDC} \right) \\ \left( \alpha \right)//SC\\ SC \subset \left( {SDC} \right) \end{array} \right. \Rightarrow \left( \alpha \right) \cap \left( {SDC} \right) = NP//SC\)  \(\left( {P \in CD} \right)\).

+ \(\left\{ \begin{array}{l} P \in\left( \alpha \right) \cap \left( {ABCD} \right) \\ \left( \alpha \right)//AD\\ AD \subset \left( {ABCD} \right) \end{array} \right. \Rightarrow \left( \alpha \right) \cap \left( {ABCD} \right) = PQ//AD\)  \(\left( {Q \in AB} \right)\).

+ \(\left( \alpha \right) \cap \left( {SAB} \right) = MQ\).

Vậy thiết diện cần tìm là hình thang MNPQ.

Bài 1: Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AD và BC = \(\frac{1}{2}\) AD. Gọi O là giao điểm của hai đường chéo AC và BD, G là trọng tâm tam giác SCD.

a) Chứng minh rằng OG // (SBC).

b) Cho K là trung điểm của SD. Chứng minh rằng CK  // (SAB).

c) Gọi I là điểm nằm trên đoạn SC sao cho 2SC = 3SI. Chứng minh rằng SA // (BID).

Bài 2: Cho tứ diện ABCD. Trên BC lấy điểm M bất kì (M khác B, C). Tìm thiết diện của mặt phẳng (P) với tứ diện ABCD nếu (P) đi qua M và song song với AC và BD. Thiết diện đó là hình gì?

Bài 3: Cho hình chóp S.ABCD. K, H là hai điểm trên AB, CD, (P) là mặt phẳng qua KH và song song với SA.

a) Tìm giao tuyến của (P) với các mặt phẳng (SAB) và (SAC).

b) Xác định thiết diện của hình chóp với mặt phẳng (P).

c) Tìm điều kiện của KH để thiết diện là hình thang.

Bài 4: Cho tứ diện đều ABCD cạnh a. M và P là hai điểm bất kì trên AD và BC sao cho MA = PC = x (0 < x < a). Mặt phẳng (Q) qua MP song song với CD cắt tứ diện theo một thiết diện.

a) Chứng minh thiết diện là hình thang cân.

b) Tìm x để diện tích thiết diện nhỏ nhất.

Bài 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi d là giao tuyến của hai mặt phẳng (SAB) và (SCD). Khẳng định nào sau đây là đúng?

A. d qua S và song song với AB.

B. d qua S và song song với BC.

C. d qua S và song song với AD.

D. d qua S và song song với AC.

Bài 2: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. I, J lần lượt là trọng tâm tam giác SBC và SAD. E, F lần lượt là trung điểm của BC và AD. Tìm khẳng định đúng?

A. IJ // (SBD).

B. IJ // (SEF).

C. IJ // (SAB).

D. IJ // (SAD).

Bài 3: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, I là trung điểm cạnh SC. Khẳng định nào sau đây sai?

A. IO song song (SAB).

B. IO song song (SAD).

C. (IBD) \( \cap \) (SAC) =IO.

D. Mặt phẳng (IBD) cắt khối chóp S.ABCD theo thiết diện là một tứ giác.

Bài 4: Cho tứ diện ABCD, gọi M, N, P lần lượt là trung điểm của AB, BC, CD. Thiết diện tạo bởi tứ diện và mặt phẳng (MNP) là hình gì?

A. Tam giác.

B. Hình bình hành.

C. Hình ngũ giác.

D. Tam giác cân.

Bài 5: Cho tứ diện đều ABCD cạnh a và G là trọng tâm tam giác ABC. Cắt tứ diện bởi mặt phẳng (P) qua G và song song với mặt phẳng (BCD) thì diện tính thiết diện bằng bao nhiêu?

A. \(\frac{{{a^2}\sqrt 3 }}{4}\).

B. \(\frac{{{a^2}\sqrt 3 }}{9}\).

C. \(\frac{{{a^2}\sqrt 3 }}{16}\).

D. \(\frac{{{a^2}\sqrt 3 }}{18}\).

Qua bài học này các em cần nắm được các nội dung sau:

- Khái niệm và điều kiện đường thẳng song song với mặt phẳng.

- Xác định được vị trí tương đối giữa đường thẳng và mặt phẳng.

- Biết dựa vào các định lí để chứng minh một đường thẳng song song với một mặt phẳng, xác định giao tuyến hai mặt phẳng trong một số trường hợp đơn giản.