Toán 11 Chương 2 Bài 1: Đại cương về đường thẳng và mặt phẳng
Sau đây mời các em học sinh lớp 11 cùng tìm hiểu bài Đại cương về đường thẳng và mặt phẳng. Bài giảng được eLib biên soạn khái quát về các lý thuyết cần nhớ, cùng với một số bài tập minh họa có hướng dẫn giải chi tiết sẽ giúp các em dễ dàng nắm vững được nội dung bài học, qua đó giúp các em ôn tập và củng cố lại kiến thức của bài.
Mục lục nội dung

1. Tóm tắt lý thuyết
1.1. Khái niệm mở đầu
a. Mặt phẳng
- Trang giấy, mặt bảng đen, mặt hồ lặng gió, mặt bàn... cho ta hình ảnh một phần của mặt phẳng.
- Mặt phẳng không có bề dày và không có giới hạn.
- Biểu diễn mặt phẳng: dùng hình bình hành hay một miến góc và ghi tên của mặt phẳng vào một góc của hình biểu diễn.

- Kí hiệu mặt phẳng: dùng chữ cái in hoa hoặc chữ cái Hi Lạp trong dấu ngoặc ( ).
VD: mặt phẳng (P), mặt phẳng (Q), mặt phẳng \(\left( \alpha \right)\), mặt phẳng (β) hoặc mp (P), mp (Q), mp \(\left( \alpha \right)\), mp (β) hoặc (P), (Q), \(\left( \alpha \right)\), (β)…
b. Điểm thuộc mặt phẳng
- Khi điểm A thuộc mặt phẳng \(\left( \alpha \right)\) ta nói A nằm trên \(\left( \alpha \right)\), hay \(\left( \alpha \right)\) chứa A, hay \(\left( \alpha \right)\) đi qua A, kí hiệu \(A \in \left( \alpha \right)\).
- Khi điểm B không thuộc mặt phẳng \(\left( \alpha \right)\) ta nói B nằm ngoài \(\left( \alpha \right)\), hay \(\left( \alpha \right)\) không chứa B, kí hiệu \(B \notin \left( \alpha \right)\).
c. Hình biểu diễn của mặt hình không gian
- Một số hình biểu diễn
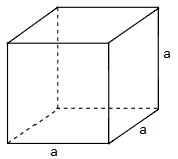
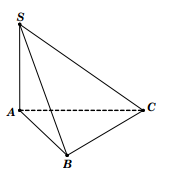
- Quy tắc vẽ hình biểu diễn của hình không gian:
+ Hình biểu diễn của đường thẳng là đường thẳng, của đoạn thẳng là đoạn thẳng.
+ Hình biểu diễn hai đường thẳng song song ( hoặc cắt nhau) được biểu diễn bằng hai đường thẳng song song ( hoặc cắt nhau).
+ Hình biểu diễn phải giữ nguyên quan hệ thuộc giữa điểm và đường thẳng.
+ Dùng nét liền ____ biểu diễn cho những đường nhìn thấy, nét đứt ----- biểu diễn cho những đường bị khuất.
1.2. Các tính chất thừa nhận
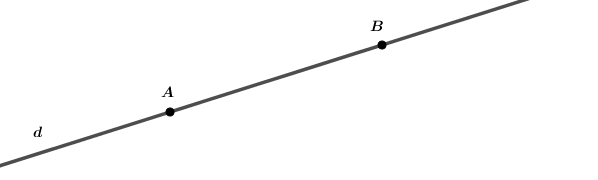
- Tính chất 1: Có một và chỉ một đường thẳng đi qua hai điểm phân biệt.
- Tính chất 2: Có một và chỉ một mặt phẳng đi qua ba điểm phân biệt.
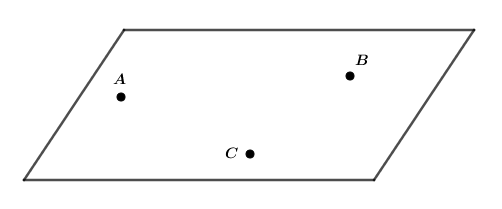
Kí hiệu: mặt phẳng qua ba điểm không thẳng hàng A, B, C là mặt phẳng (ABC) hoặc mp (ABC) hoặc (ABC).
- Tính chất 3: Nếu một đường thẳng có hai điểm chung phân biệt với một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng.
Nếu mọi điểm của đường thẳng d đều thuộc mặt phẳng \(\left( \alpha \right)\) thì ta nói đường thẳng d nằm trong \(\left( \alpha \right)\) hay \(\left( \alpha \right)\) chứa d. Kí hiệu: \(d \subset \left( \alpha \right)\) hay \(\left( \alpha \right) \supset d\).
- Tính chất 4: Tồn tại bốn điểm không cùng nằm trên một mặt phẳng.
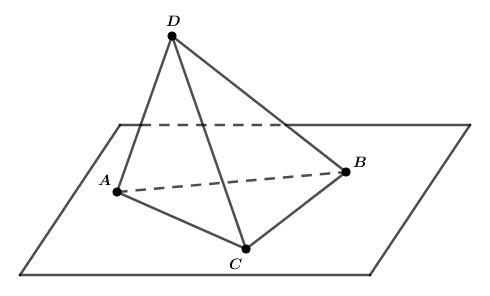
- Tính chất 5: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất chứa tất cả các điểm chung của hai mặt phẳng đó.
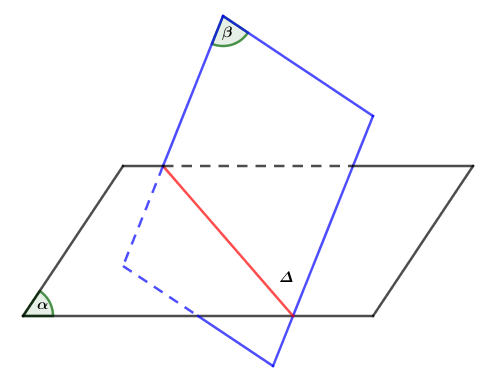
Từ đó suy ra: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng sẽ có một đường thẳng chung đi qua điểm chung ấy.
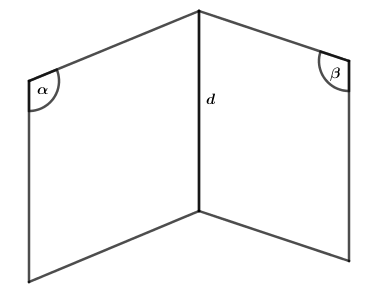
Đường thẳng chung d của hai mặt phẳng phân biệt \(\left( \alpha \right)\) và (β) được gọi là giao tuyến của \(\left( \alpha \right)\) và (β). Kí hiệu: \(d = \left( \alpha \right) \cap \left( \beta \right)\).
- Tính chất 6: Trên mỗi mặt phẳng, các kết quả đã biết trong hình học phẳng đều đúng.
1.3. Cách xác định một mặt phẳng
Ba cách xác định mặt phẳng
- Mặt phẳng được hoàn toàn xác định khi biết nó đi qua ba điểm không thẳng hàng.
.png)
Ba điểm A, B, C được kí hiệu là mp (ABC) hay (ABC).
- Mặt phẳng được hoàn toàn xác định khi biết nó đi qua một điểm và chứa một đường thẳng không đi qua điểm đó.
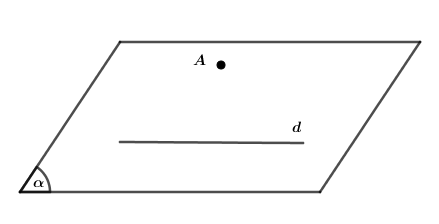
Cho đường thẳng d và điểm A không thuộc d. Kí hiệu là mp (A,d), hoặc mp (d,A) hay (d,A).
- Mặt phẳng được hoàn toàn xác định khi biết nó chứa hai đường thẳng cắt nhau.
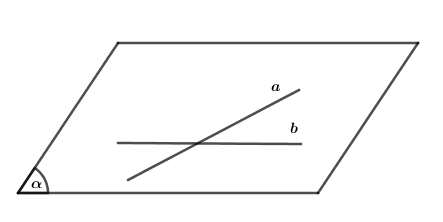
Cho hai đường thẳng cắt nhau a và b. Kí hiệu là mp (a,b) hay (a,b) hoặc mp (b,a) hay (b,a).
1.4. Hình chóp và hình tứ diện
Cho đa giác \({A_1}{A_2}...{A_n}\) và cho điểm S nằm ngoài mặt phẳng chứa đa giác đó. Nối S với các đỉnh \({A_1},{A_2},...,{A_n}\) ta được n miền đa giác \(S{A_1}{A_2},S{A_2}{A_3},...,S{A_{n - 1}}{A_n}\). Hình gồm n tam giác đó và đa giác \({A_1}{A_2}...{A_n}\) được gọi là hình chóp \(S{A_1}{A_2}...{A_n}\).
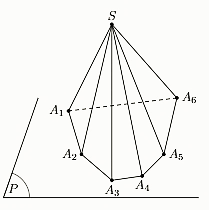
- Trong đó:
+ Điểm S gọi là đỉnh của hình chóp.
+ Đa giác \({A_1}{A_2}...{A_n}\) gọi là mặt đáy của hình chóp.
+ Các đoạn thẳng \({A_1}{A_2},{A_2}{A_3},...,{A_{n - 1}}{A_n}\) gọi là các cạnh đáy của hình chóp.
+ Các đoạn thẳng \(S{A_1},S{A_2},...,S{A_n}\) gọi là các cạnh bên của hình chóp.
+ Các miền tam giác \(S{A_1}{A_2},S{A_2}{A_3},...,S{A_{n - 1}}{A_n}\) gọi là các mặt bên của hình chóp.
- Nếu đáy của hình chóp là một miền tam giác, tứ giác, ngũ giác,…thì hình chóp tương ứng gọi là hình chóp tam giác, hình chóp tứ giác, hình chóp ngũ giác,...
- Hình chóp tứ giác còn được gọi là hình tứ diện.
- Hình tứ diện có bốn mặt là những tam giác đều hay có tất cả các cạnh bằng nhau được gọi là hình tứ diện đều.
- Thiết diện của hình chóp cắt bởi mặt phẳng (MNPQ) là một đa giác mà mỗi cạnh của nó là một đoạn giao tuyến của mặt phẳng (MNPQ) với một mặt của hình chóp.
2. Bài tập minh họa
Bài 1: Cho hình chóp S.ABCD có đáy là tứ giác có các cặp cạnh đối không song song, điểm M thuộc cạnh SA. Tìm giao tuyến của các cặp mặt phẳng sau:
a. (SAC) và (SBD).
b. (SAC) và (MBD).
c. (MBC) và (SAD).
d. (SAB) và (SCD).
Hướng dẫn giải
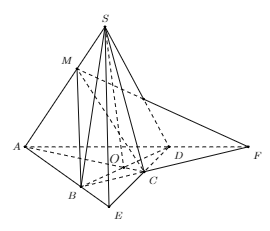
a. Trong (ABCD), gọi O là giao điểm của AC và BD.
Ta có:
\(\left\{ \begin{array}{l} O \in AC \subset \left( {SAC} \right)\\ O \in BD \subset \left( {SBD} \right) \end{array} \right. \Rightarrow O \in \left( {SAC} \right) \cap \left( {SBD} \right)\).
Lại có \(S \in \left( {SAC} \right) \cap \left( {SBD} \right)\).
Vậy \(\left( {SAC} \right) \cap \left( {SBD} \right) = SO\).
b. Vì O là giao điểm của AC và BD nên
\(\left\{ \begin{array}{l} O \in AC \subset \left( {SAC} \right)\\ O \in BD \subset \left( {MBD} \right) \end{array} \right. \Rightarrow O \in \left( {SAC} \right) \cap \left( {MBD} \right)\).
Lại có
\(\left\{ \begin{array}{l} M \in SA \subset \left( {SAC} \right)\\ M \in \left( {MBD} \right) \end{array} \right. \Rightarrow M \in \left( {SAC} \right) \cap \left( {MBD} \right)\).
Vậy \(\left( {SAC} \right) \cap \left( {MBD} \right) = OM\).
c. Trong (ABCD), gọi F là giao điểm của BC và AD.
Ta có:
\(\left\{ \begin{array}{l} F \in BC \subset \left( {MBC} \right)\\ F \in AD \subset \left( {SAD} \right) \end{array} \right. \Rightarrow F \in \left( {MBC} \right) \cap \left( {SAD} \right)\).
Lại có:
\(\left\{ \begin{array}{l} M \in SA \subset \left( {SAD} \right)\\ M \in \left( {MBC} \right) \end{array} \right. \Rightarrow M \in \left( {MBC} \right) \cap \left( {SAD} \right)\).
Vậy \(\left( {MBC} \right) \cap \left( {SAD} \right) = FM\).
d. Trong (ABCD), gọi E là giao điểm của AB và CD.
Ta có:
\(\left\{ \begin{array}{l} E \in AB \subset \left( {SAB} \right)\\ E \in CD \subset \left( {SCD} \right) \end{array} \right. \Rightarrow E \in \left( {SAB} \right) \cap \left( {SCD} \right)\).
Dễ thấy \(S \in \left( {SAB} \right) \cap \left( {SCD} \right)\).
Vậy \(\left( {SAB} \right) \cap \left( {SCD} \right) = SE\).
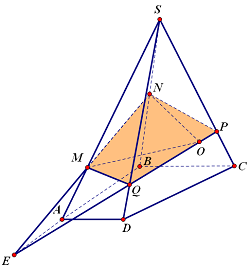
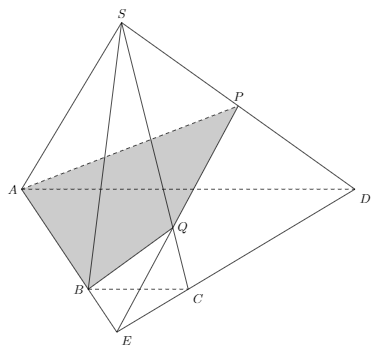
Bài 2: Cho hình chóp tứ giác S.ABCD, có đáy là hình thang với AD là đáy lớn và P là một điểm trên cạnh SD. Thiết diện của hình chóp cắt bởi mặt phẳng (PAB) là hình gì?
Hướng dẫn giải:
Trong (ABCD), gọi \(E = AB \cap CD\).
Trong (SCD), gọi \( Q = SC \cap EP\).
Ta có \(E \in AB\) nên \(EP \subset \left( {ABP} \right) \Rightarrow Q \in \left( {ABP} \right)\), do đó \(Q = SC \cap \left( {ABP} \right)\). Thiết diện là tứ giác ABQP.
3. Luyện tập
3.1. Bài tập tự luận
Bài 1: Cho tứ diện ABCD, O là một điểm thuộc miền trong tam giác BCD, M là điểm trên đoạn AO.
a. Tìm giao tuyến của (MCD) với các mặt phẳng (ABC), (ABD).
b. Gọi I, J là các điểm tướng ứng trên các cạnh BC và BD sao cho IJ không song song với CD. Tìm giao tuyến của hai mặt phẳng (JMI) và (ACD).
Bài 2: Cho hình chóp S.ABCD có đáy là một hình bình hành tâm O. Gọi M, N, P là ba điểm trên các cạnh AD, CD, SO. Xác định thiết diện của hình chóp với mặt phẳng (MNP).
3.2. Bài tập trắc nghiệm
Bài 1: Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác BCD. Giao tuyến của mặt phẳng (ACD) và (GAB) là:
A. AM (M là trung điểm AB).
B. AN (N là trung điểm CD).
C. AH ( H là hình chiếu của B trên CD).
D. AK (K là hình chiếu của C trên BD).
Bài 2: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC, CD. Giao tuyến của hai mặt phẳng (MBD) và (ABN) là:
A. Đường thẳng MN.
B. Đường thẳng AM.
C. Đường thẳng BG (G là trọng tâm tam giác ACD).
D. Đường thẳng AH (H là trực tâm tam giác ACD).
Bài 3: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J lần lượt là trung điểm SA, SB. Khẳng định nào sau đây sai?
A. IJCD là hình thang.
B. \(\left( {SAB} \right) \cap \left( {IBC} \right) = IB\).
C. \(\left( {SBD} \right) \cap \left( {JCD} \right) \in J\).
D. \(\left( {IAC} \right) \cap \left( {JBD} \right) = AO\) (O là tâm ABCD).
Bài 4: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm các cạnh AB và AC, E là điểm trên cạnh CD với ED = 3EC. Thiết diện tạo bởi (MNE) với tứ diện ABCD là:
A. Tam giác MNE.
B. Tứ giác MNEF với F là điểm bất kì trên cạnh BD.
C. Hình bình hành MNEF với F là điểm trên cạnh BD mà EF // BC.
D. Hình thang MNEF với F là điểm trên cạnh BD và EF // BC.
3.3. Trắc nghiệm Online
Các em hãy luyện tập bài trắc nghiệm Đại cương về đường thẳng và mặt phẳng Toán 11 sau để nắm rõ thêm kiến thức bài học.
4. Kết luận
Qua bài học này, các em cần nắm được các nội dung sau:
- Nắm vững các khái niệm mở đầu, các tính chất thừa nhận, cách xác định mặt phẳng, hình chóp và hình tứ diện.
- Vẽ được hình biểu diễn của một số hình không gian đơn giản.
- Xác định được: giao tuyến của hai mặt phẳng, thiết diện của hình chóp với mặt phẳng.
Tham khảo thêm
- doc Toán 11 Chương 2 Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song
- doc Toán 11 Chương 2 Bài 3: Đường thẳng và mặt phẳng song song
- doc Toán 11 Chương 2 Bài 4: Hai mặt phẳng song song
- doc Toán 11 Chương 2 Bài 5: Phép chiếu song song. Hình biểu diễn của một hình không gian
- doc Toán 11 Ôn tập chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
