Toán 11 Chương 2 Bài 4: Hai mặt phẳng song song
Để giúp các em học sinh lớp 11 học hiệu quả môn Toán, đội ngũ eLib đã biên soạn và tổng hợp nội dung bài Hai mặt phẳng song song. Tài liệu gồm kiến thức cần nhớ và các dạng toán có liên quan với hướng dẫn giải chi tiết, giúp các em học tập và củng cố thật tốt kiến thức. Mời các em cùng tham khảo.
Mục lục nội dung

Toán 11 Chương 2 Bài 4: Hai mặt phẳng song song
1. Tóm tắt lí thuyết
1.1. Định nghĩa
Hai mặt phẳng (α), (β) được gọi là song song với nhau nếu chúng không có điểm chung.
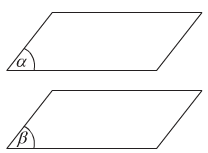
Kí hiệu: (α) // (β) hay (β) // (α).
1.2. Tính chất
- Định lí 1: Nếu mặt phẳng chứa hai đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng thì song song với .
.png)
{a,b⊂(α)a,b//(β)⇒(α)//(β)
- Định lí 2: Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chỉ một mặt phẳng song song với mặt phẳng đã cho.
.png)
+ Hệ quả 1: Nếu đường thẳng d song song với mặt phẳng (α) thì qua d có duy nhất một mặt phẳng song song với (α).
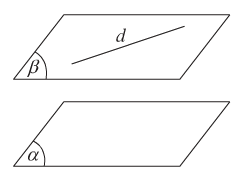
+ Hệ quả 2: Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì song song với nhau.
+ Hệ quả 3: Cho điểm A không nằm trên mặt phẳng (α). Mọi đường thẳng đi qua A và song song với (α) đều nằm trong mặt phẳng đi qua A và song song với (α).
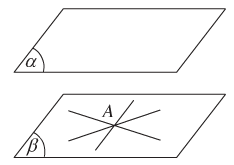
- Định lí 3: Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.
.png)
{(α)//(β)(α)∩(γ)=a(β)∩(γ)=b⇒a//b
+ Hệ quả: Hai mặt phẳng song song chắn trên hai cát tuyến song song những đoạn thẳng bằng nhau.
.png)
1.3. Định lí Ta – lét
- Định lí 4: Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì những đoạn thẳng tương ứng tỉ lệ.
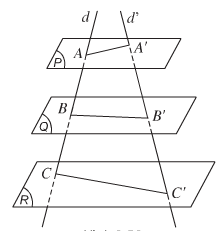
Nếu d, d’ là hai cát tuyến bất kì cắt ba mặt phẳng song song (α), (β), (γ) lần lượt tại các điểm A, B, C và A’, B’, C’ thì ABA′B′=BCB′C′=CAC′A′.
1.4. Hình lăng trụ và hình hộp
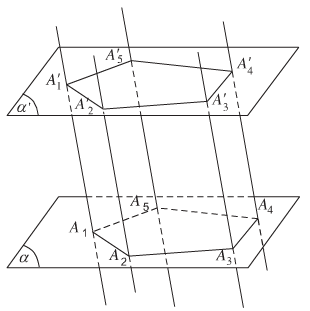
- Hình gồm hai đa giác A1A2...An, A′1A′2...A′n và các hình bình hành A1A′1A2A′2, A2A′2A3A′3,…, AnA′nA1A′1 được gọi là hình lăng trụ và được kí hiệu là A1A2...An.A′1A′2...A′n.
+ Hai đa giác A1A2...An và A′1A′2...A′n được gọi là mặt đáy của hình lăng trụ.
+ Các hình bình hành A1A′1A2A′2, A2A′2A3A′3,…, AnA′nA1A′1 được gọi là các mặt bên của hình lăng trụ.
+ Các đỉnh của hai đa giác được gọi là các đỉnh của hình lăng trụ.
- Nhận xét:
+ Các cạnh bên của hình lăng trụ bằng nhau và song song với nhau.
+ Các mặt bên của hình lăng trụ là các hình bình hành.
+ Hai đáy của hình lăng trụ là hai đa giác bằng nhau.
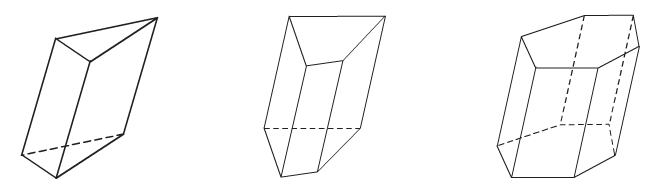
Hình lăng trụ tam giác Hình lăng trụ tứ giác Hình lăng trụ lục giác
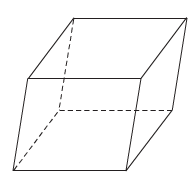
+ Hình lăng trụ có đáy là hình bình hành được gọi là hình hộp.
1.5. Hình chóp cụt
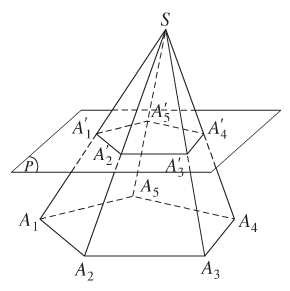
- Định nghĩa: Cho hình chóp S.A1A2...An; một mặt phẳng (P) không qua đỉnh, song song với mặt phẳng đáy của hình chóp cắt các cạnh SA1, SA2,.., SAn lần lượt tại A′1, A′2,…, A′n. Hình tạo bởi thiết diện A′1A′2...A′n và đáy A1A2...An của hình chóp cùng với các tứ giác A′1A′2A2A1, A′2A′3A3A2,…, A′nA′1A1An gọi là hình chóp cụt.
+ Đáy A1A2...An của hình chóp gọi là đáy lớn của hình chóp cụt.
+ Thiết diện A′1A′2...A′n gọi là đáy nhỏ của hình chóp cụt.
+ Các tứ giác A′1A′2A2A1, A′2A′3A3A2,…, A′nA′1A1An gọi là các mặt bên của hình chóp cụt.
+ Các đoạn thẳng A1A′1, A2A′2,…, AnA′n gọi là các cạnh bên của hình chóp cụt.
+ Tùy theo đáy là tam giác, tứ giác, ngũ giác,… ta có hình chóp cụt tam giác, hình chóp cụt tứ giác, hình chóp cụt ngũ giác,…
- Tính chất:
+ Hai đáy là hai đa giác có các cạnh tương ứng song song và các tỉ số các cặp cạnh tương ứng bằng nhau.
+ Các mặt bên là những hình thang.
+ Các đường thẳng chứa các cạnh bên đồng quy tại một điểm.
2. Bài tập minh họa
Bài 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, O là tâm của đáy. Gọi E, F lần lượt là trung điểm của SA, SB. Chứng minh (OEF) // (SCD).
Hướng dẫn giải:
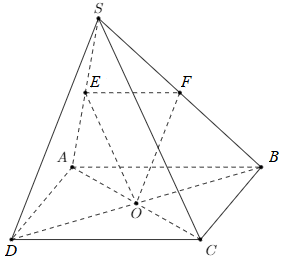
Tam giác SBD có O, F lần lượt là trung điểm của BD, SB.
Suy ra OF là đường trung bình của tam giác SBD do đó OF // SD.
Ta có: {OF//SDSD⊂(SCD)⇒OF//(SCD) (1).
Tam giác SAC có O, E lần lượt là trung điểm của AC, SA.
Suy ra OE là đường trung bình của tam giác SAC do đó OE // SC.
Ta có {OE//SCSC⊂(SCD)⇒OE//(SCD) (2).
Từ (1) và (2) suy ra (OEF) // (SCD).
Bài 2: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm H. Mặt phẳng (P) đi qua H và song song với (SAB). Tìm giao tuyến của mặt phẳng (P) với các mặt phẳng sau:
a) Mặt phẳng (ABCD).
b) Mặt phẳng (SBC).
Hướng dẫn giải:
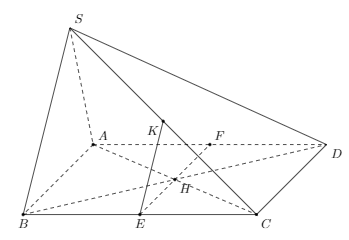
a) Ta có:
{(P)//(SAB)(ABCD)∩(SAB)=ABP∈(P)∩(ABCD)⇒(P)∩(ABCD)=EF với EF qua H và song song với AB.
b) Ta có:
{(P)//(SAB)(SBC)∩(SAB)=SBE∈(P)∩(SBC)⇒(P)∩(SBC)=EK với EK // SB và K∈SC.
Bài 3: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Tam giác SBD đều, I là điểm bất kì trên cạnh AC (khác A, C). Mặt phẳng (P) song song (SBD) và đi qua I. Thiết diện của (P) và hình chóp là hình gì?
Hướng dẫn giải:
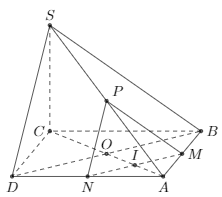
Gọi MN là đoạn thẳng giao tuyến của mặt phẳng (P) và mặt đáy (ABCD). Vì (P) // (SBD), (P)∩(ABCD)=MN và (SBD) ∩ (ABCD) = MN suy ra MN // BD.
Lập luận tương tự, ta có:
(P) cắt mặt phẳng (SAD) theo đoạn giao tuyến NP với NP // SD.
(P) cắt mặt phẳng (SAB) theo đoạn giao tuyến MP với MP // SB.
Vậy tam giác MNP đồng dạng với tam giác SBD nên thiết diện của (P) và hình chóp S.ABCD là tam giác đều MNP.
3. Luyện tập
3.1. Bài tập tự luận
Bài 1: Cho hình chóp S.ABCD có đáy là hình thang (AB // CD và AB = 2CD), I là giao điểm của AC và BD. Gọi M là trung điểm của SD, E là trung điểm của CM và G là điểm đối xứng của E qua M, SE cắt CD tại K. Chứng minh (IKE) // (ADG).
Bài 2: Cho hình chóp S.ABCD có đáy là hình bình thành. Gọi M, N, P, Q, R là trung điểm của AB, SB, BG, BI, DC.
a) Chứng minh rằng (RMN) // (SAD).
b) Chứng minh rằng PQ // (SAD).
c) Tìm giao tuyến của (SAC) và (RMN).
Bài 3: Cho hình hộp ABCD.A’B’C’D’. Gọi O là tâm hình bình hành ABCD, K là trung điểm C’D’, E là trung điểm của B’O. Xác định thiết diện của hình hộp khi cắt bởi mặt phẳng (P) qua điểm K và song song mặt phẳng (EA’C’).
Bài 4: Cho hình chóp S.ABCD có đáy là hình thang, đáy lớn AB = 3a, AD = CD = a. Mặt bên (SAB) là tam giác cân đỉnh S với SA = 2a, gọi M là điểm thuộc cạnh AD. Mặt phẳng (P) đi qua M và song song với (SAB). Xác định thiết diện của hình chóp với mặt phẳng (P). Thiết diện là hình gì?
3.2. Bài tập trắc nghiệm
Bài 1: Cho hình hộp ABCD.A'B'C'D'. Gọi M và M' lần lượt là tâm của A'ABB' và D'DCC'. Hãy chọn khẳng định không đúng?
A. MM' // (ADD'A').
B. MM' và BB' đồng phẳng.
C. MM' là đường trung bình của hình bình hành.
D. →MM′=→AD.
Bài 2: Cho hình chóp S.ABC có đáy là tam giác ABC thỏa mãn AB = AC = 4, . Mặt phẳng (P) song song với (ABC) cắt đoạn SA tại M sao cho SM = 2MA. Diện tích thiết diện của (P) và hình chóp S.ABCD bằng bao nhiêu?
A. 169.
B. 149.
C. 259.
D. 1.
Bài 3: Cho hình lăng trụ ABC.A’B’C’, gọi I, J, K lần lượt là trọng tâm tam giác ABC, tam giác ACC’ và tam giác AB’C’. Mặt phẳng nào sau đây song song với (IJK)?
A. (BC’A).
B. (AA’B).
C. (BB’C).
D. (CC’A).
Bài 4: Cho hình hộp ABCD.A’B’C’D’ và điểm M nằm giữa hai điểm A và B. Gọi (P) là mặt phẳng đi qua M và song song với mặt phẳng (AB’D’). Mặt phẳng (P) cắt hình hộp theo thiết diện là hình gì?
A. Hình ngũ giác.
B. Hình lục giác.
C. Hình tam giác.
D. Hình tứ giác.
Bài 5: Cho hình nón cụt tam giác ABC.A’B’C’ có 2 đáy là 2 tam giác vuông tại A và A’ và có ACA′C′=13. Khi đó tỉ số diện tích SΔABCSΔA′B′C′ bằng:
A. 13.
B. 16.
C. 19.
D. 3.
3.3. Trắc nghiệm Online
Các em hãy luyện tập bài trắc nghiệm Hai mặt phẳng song song Toán 11 sau để nắm rõ thêm kiến thức bài học.
4. Kết luận
Qua bài học này các em cần nắm được những nội dung sau:
- Khái niệm và điều kiện hai mặt phẳng song song; định lí Ta – lét trong không gian; khái niệm hình lăng trụ, hình hộp, hình chóp cụt.
- Làm được các bài toán: chứng minh hai mặt phẳng song song; vẽ được hình biểu diễn của hình hộp, hình lăng trụ, hình chóp, hình chóp cụt có đáy là tam giác, tứ giác.
Tham khảo thêm
- doc Toán 11 Chương 2 Bài 1: Đại cương về đường thẳng và mặt phẳng
- doc Toán 11 Chương 2 Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song
- doc Toán 11 Chương 2 Bài 3: Đường thẳng và mặt phẳng song song
- doc Toán 11 Chương 2 Bài 5: Phép chiếu song song. Hình biểu diễn của một hình không gian
- doc Toán 11 Ôn tập chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song

