Toán 11 Ôn tập chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song

a) Khái niệm mở đầu

- Trang giấy, mặt bảng đen, mặt hồ lặng gió, mặt bàn... cho ta hình ảnh một phần của măt phẳng.

- Mặt phẳng không có bề dày và không có giới hạn.

- Kí hiệu mặt phẳng: dùng chữ cái in hoa hoặc chữ cái Hi Lạp trong dấu ngoặc ( ).

- Khi điểm A thuộc mặt phẳng \(\left( \alpha \right)\) ta nói A nằm trên \(\left( \alpha \right)\), hay \(\left( \alpha \right)\) chứa A, hay \(\left( \alpha \right)\) đi qua A, kí hiệu \(A \in \left( \alpha \right)\).

- Khi điểm B không thuộc mặt phẳng \(\left( \alpha \right)\) ta nói B nằm ngoài \(\left( \alpha \right)\), hay \(\left( \alpha \right)\) không chứa B, kí hiệu \(B \notin \left( \alpha \right)\).

- Quy tắc vẽ hình biểu diễn của hình không gian

+ Hình biểu diễn của đường thẳng là đường thẳng, của đoạn thẳng là đoạn thẳng.

+ Hình biểu diễn hai đường thẳng song song (hoặc cắt nhau) được biểu diễn bằng hai đường thẳng song song (hoặc cắt nhau).

+ Hình biểu diễn phải giữ nguyên quan hệ thuộc giữa điểm và đường thẳng.

+ Dùng nét liền ____ biểu diễn cho những đường nhìn thấy, nét đứt ----- biểu diễn cho những đường bị khuất.

b) Các tính chất thừa nhận

- Tính chất 1: Có một và chỉ một đường thẳng đi qua hai điểm phân biệt.

- Tính chất 2: Có một và chỉ một mặt thẳng đi qua ba điểm phân biệt.

- Tính chất 3: Nếu một đường thẳng có hai điểm chung phân biệt với một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng.

- Tính chất 4: Tồn tại bốn điểm không cùng nằm trên một mặt phẳng.

- Tính chất 5: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất chứa tất cả các điểm chung của hai mặt phẳng đó.

- Tính chất 6: Trên mỗi mặt phẳng, các kết quả đã biết trong hình học phẳng đều đúng.

c) Cách xác định một mặt phẳng (3 cách)

- Mặt phẳng được hoàn toàn xác định khi biết nó đi qua ba điểm không thẳng hàng.

- Mặt phẳng được hoàn toàn xác định khi biết nó đi qua một điểm và chứa một đường thẳng không đi qua điểm đó.

- Mặt phẳng được hoàn toàn xác định khi biết nó chứa hai đường thẳng cắt nhau.

d) Hình chóp và hình tứ diện

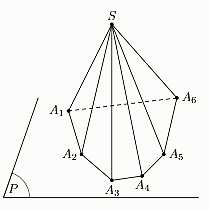
- Nếu đáy của hình chóp là một miền tam giác, tứ giác, ngũ giác,… thì hình chóp tương ứng gọi là hình chóp tam giác, hình chóp tứ giác, hình chóp ngũ giác.

- Hình chóp tứ giác còn được gọi là hình tứ diện.

- Hình tứ diện có bốn mặt là những tam giác đều hay có tất cả các cạnh bằng nhau được gọi là hình tứ diện đều.

a) Vị trí tương đối của hai đường thẳng trong không gian

- Trường hợp 1: a và b đồng phẳng

+ a cắt b (a và b có một điểm chung).

+ a // b (a và b không có điểm chung).

+ a trùng b.

- Trường hợp 2: a và b chéo nhau (a và b không nằm trên cùng một mặt phẳng).

b) Tính chất

- Định lí 1: Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có một và chỉ một đường thẳng song song với đường thẳng đã cho.

- Định lí 2: Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song với nhau.

- Hệ quả: Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

- Định lí 3: Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.

a) Vị trí tương đối của đường thẳng và mặt phẳng

- d // \(\left( \alpha \right)\) (d và \(\left( \alpha \right)\) không có điểm chung).

- d và \(\left( \alpha \right)\) cắt nhau (d và \(\left( \alpha \right)\) có 1 điểm chung).

- d \( \subset \left( \alpha \right)\) (d và \(\left( \alpha \right)\) có từ hai điểm chung trở lên).

b) Tính chất

- Định lí 1: Nếu đường thẳng d không nằm trong mặt phẳng \(\left( \alpha \right)\) và d song song với đường thẳng d’ nằm trong \(\left( \alpha \right)\) thì d song song với \(\left( \alpha \right)\).

- Định lí 2: Cho đường thẳng a song song với mặt phẳng \(\left( \alpha \right)\). Nếu mặt phẳng \(\left( \alpha \right)\) chứa a và cắt \(\left( \alpha \right)\) theo giao tuyến b thì b song song với a.

- Hệ quả: Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.

- Định lí 3: Cho hai đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.

a) Định nghĩa

Hai mặt phẳng \(\left( \alpha \right)\), \(\left( \beta \right)\) được gọi là song song với nhau nếu chúng không có điểm chung.

Kí hiệu: \(\left( \alpha \right)\) // \(\left( \beta \right)\) hay \(\left( \beta \right)\) // \(\left( \alpha \right)\).

b) Tính chất

- Định lí 1: Nếu mặt phẳng \(\left( \alpha \right)\) chứa hai đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng \(\left( \beta \right)\) thì \(\left( \alpha \right)\) song song với \(\left( \beta \right)\).

- Định lí 2: Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chỉ một mặt phẳng song song với mặt phẳng đã cho.

+ Hệ quả 1: Nếu đường thẳng d song song với mặt phẳng \(\left( \alpha \right)\) thì qua d có duy nhất một mặt phẳng song song với \(\left( \alpha \right)\).

+ Hệ quả 2: Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì song song với nhau.

+ Hệ quả 3: Cho điểm A không nằm trên mặt phẳng \(\left( \alpha \right)\). Mọi đường thẳng đi qua A và song song với \(\left( \alpha \right)\) đều nằm trong mặt phẳng đi qua A và song song với \(\left( \alpha \right)\).

- Định lí 3: Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.

+ Hệ quả: Hai mặt phẳng song song chắn trên hai cát tuyến song song những đoạn thẳng bằng nhau.

c) Định lí Ta – lét

- Định lí 4: Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì những đoạn thẳng tương ứng tỉ lệ.

d) Hình lăng trụ và hình hộp

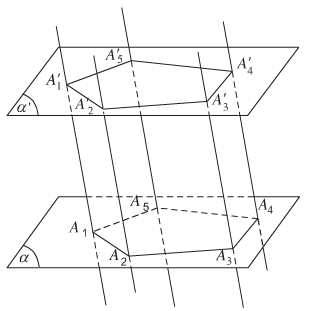
- Các cạnh bên của hình lăng trụ bằng nhau và song song với nhau.

- Các mặt bên của hình lăng trụ là các hình bình hành.

- Hai đáy của hình lăng trụ là hai đa giác bằng nhau.

- Hình lăng trụ có đáy là hình bình hành được gọi là hình hộp.

e) Hình chóp cụt

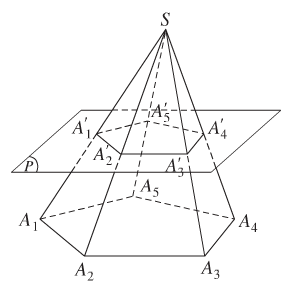
- Hai đáy là hai đa giác có các cạnh tương ứng song song và các tỉ số các cặp cạnh tương ứng bằng nhau.

- Các mặt bên là những hình thang.

- Các đường thẳng chứa các cạnh bên đồng quy tại một điểm.

a) Phép chiếu song song

Điểm M’ được gọi là hình chiếu song song của điểm M trên mặt phẳng \(\left( \alpha \right)\) theo phương \(\Delta \).

b) Các tính chất của phép chiếu song song

- Định lí 1:

+ Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.

+ Phép chiếu song song biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thành đoạn thẳng.

+ Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau.

+ Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc cùng nằm trên một đường thẳng.

c) Hình biểu diễn của một hình không gian trên mặt phẳng

- Tam giác: Một tam giác bất kì bao giờ cũng có thể coi là hình biểu diễn của một tam giác có dạng tùy ý cho trước (có thể là tam giác đều, tam giác cân, tam giác vuông,…).

- Hình bình hành: Một hình bình hành bất kì bao giờ cũng có thể coi là hình biểu diễn của một hình bình hành có dạng tùy ý cho trước (có thể là hình bình hành, hình vuông, hình thoi, hình chữ nhật,…).

- Hình thang: Một hình thang bất kì bao giờ cũng có thể coi là hình biểu diễn của một hình thang có dạng tùy ý cho trước, miễn là tỉ số độ dài hai đáy của hình biểu diễn phải bằng tỉ số độ dài hai đáy của hình thang ban đầu.

- Hình tròn: dùng hình elip để biểu diễn cho hình tròn.

Bài 1: Cho hai hình thang ABCD và ABEF có chung đáy lớn AB và không cùng nằm trong một mặt phẳng.

a) Tìm giao tuyến của các mặt phẳng sau: (AEC) và (BFD); (BCE) và (ADF).

b) Lấy điểm M là một điểm bất kì thuộc đoạn DF. Xác định giao tuyến của đường thẳng AM với mặt phẳng (BCE).

Hướng dẫn giải:

a) Gọi G là giao điểm của AC và BD, H là giao điểm của AE và BF.

Ta có (AEC) \(\cap \) (BFG) = HG.

Tương tự, gọi I là giao điểm của AD và BC, K là giao điểm của AF và BE.

Ta có (BCE) \(\cap \) (ADF) = IK.

b) Gọi N là giao điểm của AM và IK. Suy ra N là giao điểm của AM với (BCE).

Bài 2: Cho tứ diện ABCD. Gọi M là trung điểm AD, N là điểm bất kì (N khác B và C). Gọi (P) là mặt phẳng qua đường thẳng MN và song song với CD.

a) Xác định thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (P).

b) Xác định vị trí điểm N trên BC sau cho thiết diện là một hình bình hành.

Hướng dẫn giải:

a) Ta có

\(\left\{ \begin{array}{l} CD \subset \left( {ACD} \right)\\ CD//\left( P \right) \end{array} \right. \Rightarrow \left( {ACD} \right) \cap \left( P \right) = MJ\) với MJ // CD (J thuộc AC).

Tương tự, ta có \(\left( {BCD} \right) \cap \left( P \right) = NI\) với NI // Cd (I thuộc BD).

Vậy thiết diện là hình thang MINJ (MJ // NI).

b) Ta có \(MJ = \frac{{CD}}{2}\).

Vậy để hình thang MINJ là hình bình hành thì \(NI=MJ = \frac{{CD}}{2}\).

Suy ra N là trung điểm BC.

Bài 3: Cho tứ diện ABCD gọi M, N lần lượt là trung điểm của cạnh AB và CD, E là điểm chia BC theo tỉ số BE : BC = 2 : 1. Trên đoạn thẳng AM lấy điểm H. Tìm giao tuyến của (P) đi qua H và song song với (MNE). Tìm giao tuyến của:

a) (P) và (BCD).

b) (P) và (ABD).

Hướng dẫn giải:

a) Ta có:

\(\left\{ \begin{array}{l} (P)//(MNE)\\ (MNE) \cap (ABC) = ME\\ H \in(P) \cap (ABC) \end{array} \right. \Rightarrow (P) \cap (ABC) = HK\)

với \(\left\{ \begin{array}{l} HK \cap BC = K\\ HK//ME \end{array} \right.\).

Khi đó \(\left\{ \begin{array}{l} (P)//(MNE)\\ (MNE) \cap (BCD) = EN\\K \in (P) \cap (BCD) \end{array} \right. \Rightarrow (P) \cap (BCD) = KL\) 

với \(\left\{ \begin{array}{l} KL \cap CD = L\\ KL//EN \end{array} \right.\).

b) Ta có:

\(\left\{ \begin{array}{l} EN//BD\\ M \in (MNE)//(SBD) \end{array} \right. \Rightarrow (MNE)//(SBD) = MF\)

với \(\left\{ \begin{array}{l} MF \cap AD = F\\ MF//BD \end{array} \right.\).

Khi đó \(\left\{ \begin{array}{l} (P)//(MNE)\\ (MNE) \cap (ABD) = MF\\ H \in (P) \cap (ABD) \end{array} \right. \Rightarrow (P) \cap (ABD) = HG\) 

với \(\left\{ \begin{array}{l} HG \cap AD = G\\ HG//MF \end{array} \right.\)

Bài 1: Cho hình chóp S.ABCD có đáy là hình bình hành tâm O.

a) Tìm giao tuyến của (SAD) và (SBC).

b) Gọi E là trung điểm của SC. Chứng minh OE // (SAD).

c) Gọi F là điểm trên cđoạn BD sao cho 3BF = 2BD. Tìm giao điểm M của SB và (AEF). Tính tỉ số \(\frac{{SM}}{{AB}}\).

Bài 2: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi I, J lần lượt là trọng tâm tam giác SDC và SDA. Gọi M, N lần lượt là trung điểm của SC, SD.

a) Chứng minh IJ // (ABCD).

b) Chứng minh (OMN) // (SAB).

c) Tìm giao điểm của AD và (OMN).

Bài 3: Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi H, I, K, L lần lượt là trung điểm của SA, SC, OB, SD.

a) Xác định giao tuyến của (HIK) và (SBD).

b) Chứng minh Ol // (HIK).

c) Xác định thiết diện của hình chóp S.ABCD bị cắt bởi mặt phẳng (HIK).

Bài 4: Cho hình chóp S.ABCD có đáy là hình thang, đáy lớn AD = 3 BC. Gọi O là giao điểm của AC và BD, I là điểm thuộc cạnh AD thỏa DI = 2AI, J là điểm thuộc cạnh SD thỏa DJ = 2SJ.

a) Chứng minh (SAB) // (CIJ).

b) Tìm giao tuyến của (JBC) và (SAD).

c) Gọi M là điểm bất kỳ trên cạnh CD, N là giao điểm của SM và CJ, P là giao điểm của OM và AB, Q là giao điểm của OM và CI. Chứng minh SP // QN.

a) Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB là đáy lớn). Gọi M, N lần lượt là trung điểm của SB và SC. a) Tìm giao điểm của đường thẳng AN với mặt phẳng (SBD). b) Gọi ( )α là mặt phẳng qua MN và song song với CD. Xác định thiết diện của hình chóp cắt bởi mặt phẳng ( )α.

Bài 5: Cho hình chóp S.ABC. Gọi G, K, H lần lượt là trọng tâm của các tam giác SAB, SBC và ABC.

a) Chứng minh GK // (ABC). Tìm giao tuyến của (BGK) và (ABC).

b) Chứng minh (GHK) // (SAC).

c) Tìm thiết diện do mặt phẳng (GHK) cắt hình chóp. 

Bài 1: Cho hình chóp S.ABCD có đáy là hình thang ABCD (AB // CD). Khẳng định nào sau đây sai?

A. Hình chóp S.ABCD có 4 mặt bên.

B. Giao điểm của hai mặt phẳng (SAC) và (SBD) là SO (O là giao điểm của AC và BD).

C. Giao điểm của hai mặt phẳng (SAD) và (SBC) là SI (I là giao điểm của AD và BC).

D. Giao điểm của hai mặt phẳng (SAB) và (SAD) là đường trung bình của ABCD.

Bài 2: Cho tứ diện ABCD. I và J lần lượt là trung điểm của AB và AC. G là trọng tâm tam giác BCD. Giao tuyến của hai mặt phẳng (GIJ) và (BCD) là đường thẳng:

A. Qua I và song song với AB.

B. Qua J và song song với BD.

C. Qua G và song song với CD.

D. Qua G và song song với BC.

Bài 3: Cho hình chóp S.ABCD. Gọi G, E lần lượt là trọng tâm của tam giác SAD và tam giác SCD. Lấy M, N lần lượt là trung điểm của AB, BC. Xét các mệnh đề sau:

(1) Đường thẳng MN song song với mặt phẳng (GAC).

(2) Đường thẳng MN song song với mặt phẳng (DAC).

(3) Đường thẳng GE song song với mặt phẳng (AMN).

(4) Đường thẳng GE  và đường thẳng MN trùng nhau.

(5) Đường thẳng GE và đường thẳng MN song song.

Số mệnh đề sai là:

A. 0.

B. 1.

C. 2.

D. 3.

Bài 4: Cho hình lập phương ABCD.A’B’C’D’ với AC, BD là đường chéo hình vuông ABCD còn A’C’, B’D’ là đường chéo của hình vuông A’B’C’D’. Gọi O = AC \( \cap \) BD và O’ = A’C’ \( \cap \) B’D’. Điểm M thuộc đoạn O’C’ (M không trùng với O’ hoặc C’). Mặt phẳng (P) đi qua điểm M và song song với mặt phẳng (AB’D’) cắt hình lập phương theo thiết diện có số cạnh là bao nhiêu?

A. 3.

B. 4.

C. 5.

D. 6.

Bài 5: Cho hình chóp S.ABCD đáy ABCD là hình bình hành. Mặt phẳng (P) qua AB và cắt SC tại M ở giữa S và C. Khi đó hình chiếu song song của điểm C trên mặt phẳng (SAB) theo phương chiếu AD là:

A. Điểm S.

B. Điểm A

C. Điểm B.

D. Điểm khác B và thuộc SB.

Qua bài học này các em cần nắm được những nội dung sau:

- Khái niệm, định lí và hệ quả về mặt phẳng, các xác định một mặt phẳng, hình chóp và hình tứ diện, đường thẳng song song, đường thẳngchéo nhau, đường thẳng song song với mặt phẳng, hai mặt phẳng song song, phép chiếu song song.

- Nhớ và biết cách áp dụng các định nghĩa, định lí, hệ quả của các bài học để giải bài tập.