Toán 7 Chương 1 Bài 1: Hai góc đối đỉnh
Mời các em cùng tham khảo nội dung bài giảng Hai góc đối đỉnh do eLib biên soạn và tổng hợp dưới đây. Bài giảng giúp các em nắm vững lý thuyết bài học, thêm vào đó là những bài tập minh họa có hướng dẫn giải chi tiết sẽ giúp các em dễ dàng làm được các dạng bài tập ở phần này.
Mục lục nội dung

Toán 7 Chương 1 Bài 1: Hai góc đối đỉnh
1. Tóm tắt lý thuyết
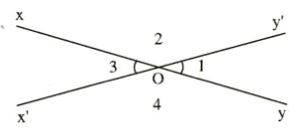
1.1. Định nghĩa
Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của mỗi cạnh góc kia.
1.2. Tính chất
Hai góc đối đỉnh thì bằng nhau ^xOyˆxOy đối đỉnh ^x′Oy′⇒^xOy=^x′Oy′.
2. Bài tập minh họa
Câu 1: Cho hai đường thẳng xy và zt cắt nhau tại O. Biết góc ^xOt lớn gấp 4 lần góc ^xOz. Tính các góc ^xOt,^tOy,^xOz và ^xOz.
Hướng dẫn giải
Ta có góc ^xOt và ^xOz là hai góc kề bù nên ^xOt+^xOz=1800 mà ^xOt=4^xOz
Do đó 4^xOt+^xOz=1800hay5^xOz=1800
Vậy ^xOz=1800:5=360
Suy ra ^xOt=4.360=1440
Các cặp góc ^yOz và ^xOt,^tOy và ^xOz là các cặp góc đổi đỉnh do đó:
^yOz=^xOt=1440^tOy=^xOz=360
Câu 2: Cho ba đường thẳng phân biệt x’x, y’y, z’z cắt nhau ở điểm O.
a. Hãy tìm 6 cặp góc đối đỉnh.
b. Có bao nhiêu cặp góc đối đỉnh không có điểm trong chung?
Hướng dẫn giải
a. Có 6 cặp góc đối đỉnh là: ^x′Oy′ và ^xOy,^y′Oz′ và ^yOz,^x′Oz′ và ^zOx,^xOy và ^xOy′,^y′Oz và ^yOz′,^z′Ox và ^zOx′.
b. Có ba cặp góc đối đỉnh không có điểm chung trong là: ^x′Oy′ và ^xOy,^y′Oz và ^yOz′,^z′Ox′ và ^zOx.
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Cho ^xOy=1000 và hai góc ^yOz và ^xOt cùng kề bù với nó. Hãy xác định hai cặp đối đỉnh và tính số đo của các góc ^zOt, ^xOt, ^yOz.
Câu 2: Cho hai đường thẳng x’x và y’y cắt nhau tại O.
a. Hỏi hai đường thẳng cắt nhau đó tạo thành mấy góc (khác góc bẹt)
b. Tính số đo mỗi góc tạo thành. Nếu biết hiệu số đo của hai góc kề bù là 300.
Câu 3: Cho góc bẹt ^AOB. Trên cùng một nửa mặt phẳng bờ AB, ta vẽ hai tia OC và OD sao cho ^AOC=^BOD=300
a. Hai góc ^AOC và ^BOD có phải là hai góc đối đỉnh không?
b. Vẽ tia OE sao cho tia OB là tia phân giác của góc ^DOE. Hai góc ^AOC và ^BOE có phải là hai góc đối đỉnh không?
3.2. Bài tập trắc nghiệm
Câu 1: Hai góc đối đỉnh là hai góc có:
A. 1 cạnh của góc này là tia đối của 1 cạnh của góc
B. mỗi cạnh của góc này là tia đối của 1 cạnh của góc kia
C. tổng của hai góc bằng 1800
D. Số đo của chúng bằng nhau
Câu 2: Hai góc đối đỉnh thì:
A. bằng nhau
B. bù nhau
C. kề, bù nhau
D. cả 3 câu trên đều sai
Câu 3: Cho đường thẳng c cắt hai đường thẳng a, b thì:
A. hai góc đồng vị bằng nhau
B. hai góc trong cùng phía bù nhau
C. hai góc so le trong bằng nhau
D. cả 3 câu trên đêu sai
Câu 4: Hai tia phân giác của hai góc đối đỉnh là:
A. Hai tia trùng nhau
B. Hai tia vuông góc
C. Hai tia song song
D. Hai tia đối nhau
Câu 5: Chọn câu trả lời sai. Hai đường thẳng xx' và bb' cắt nhau tạI O và ^xOy=60o.
A. ^x′Oy′=60o
B. ^x′Oy=120o
C. ^xOy′=120o
D. ^x′Oy′=2^xOy
4. Kết luận
Qua bài học này, các em cần nắm được những nội dung sau:
-
Định nghĩa và tính chất hai góc đối đỉnh.
-
Áp dụng giải được các bài tập liên quan.
Tham khảo thêm
- doc Toán 7 Chương 1 Bài 2: Hai đường thẳng vuông góc
- doc Toán 7 Chương 1 Bài 3: Các góc tạo bởi một đường thẳng cắt hai đường thẳng
- doc Toán 7 Chương 1 Bài 4: Hai đường thẳng song song
- doc Toán 7 Chương 1 Bài 5: Tiên đề Ơ-clit về đường thẳng song song
- doc Toán 7 Chương 1 Bài 6: Từ vuông góc đến song song
- doc Toán 7 Chương 1 Bài 7: Định lí
.JPG)
.JPG)

