Toán 7 Chương 3 Bài 9: Tính chất ba đường cao của tam giác

1. Tóm tắt lý thuyết

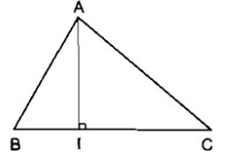
- Trong một tam giác, đoạn vuông góc kẻ từ một đỉnh đến đường thẳng chứa cạnh đối diện gọi là đường cao của tam giác đó.

Ví dụ: Đoạn thẳng AI là một đường cao của tam giác ABC, còn nói AI là đường cao xuất phát từ đỉnh A (của tam giác ABC).

- Mỗi tam giác có ba đường cao.

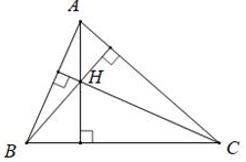
Định lý: Ba đường cao của tam giác cùng đi qua một điểm. Điểm đó gọi là trực tâm của tam giác.

Ví dụ: H là giao điểm ba đường cao của tam giác ABC. H là trực tâm của tam giác ABC

- Trong tam giác cân, đường trung trực ứng với cạnh đáy đồng thời là đường cao xuất phát từ đỉnh của tam giác đó.

- Trong tam giác đều, các điểm: trọng tâm, trực tâm, điểm cách đều ba đỉnh điểm cách đều ba cạnh là bốn điểm trùng nhau.

Nhận xét: Nếu hai trong bốn loại đường trên trùng nhau thì tam giác đó là tam giác cân.

2. Bài tập minh họa

Câu 1: Cho \(\Delta ABC\) cân ở A. Qua A kẻ đường thẳng d song song với đáy BC. Các đường phân giác của góc B và của góc C lần lượt cắt d tại E và F. Chứng minh rằng:

a) d là phân giác ngoài của góc A.

b) AE = AF

Hướng dẫn giải

​

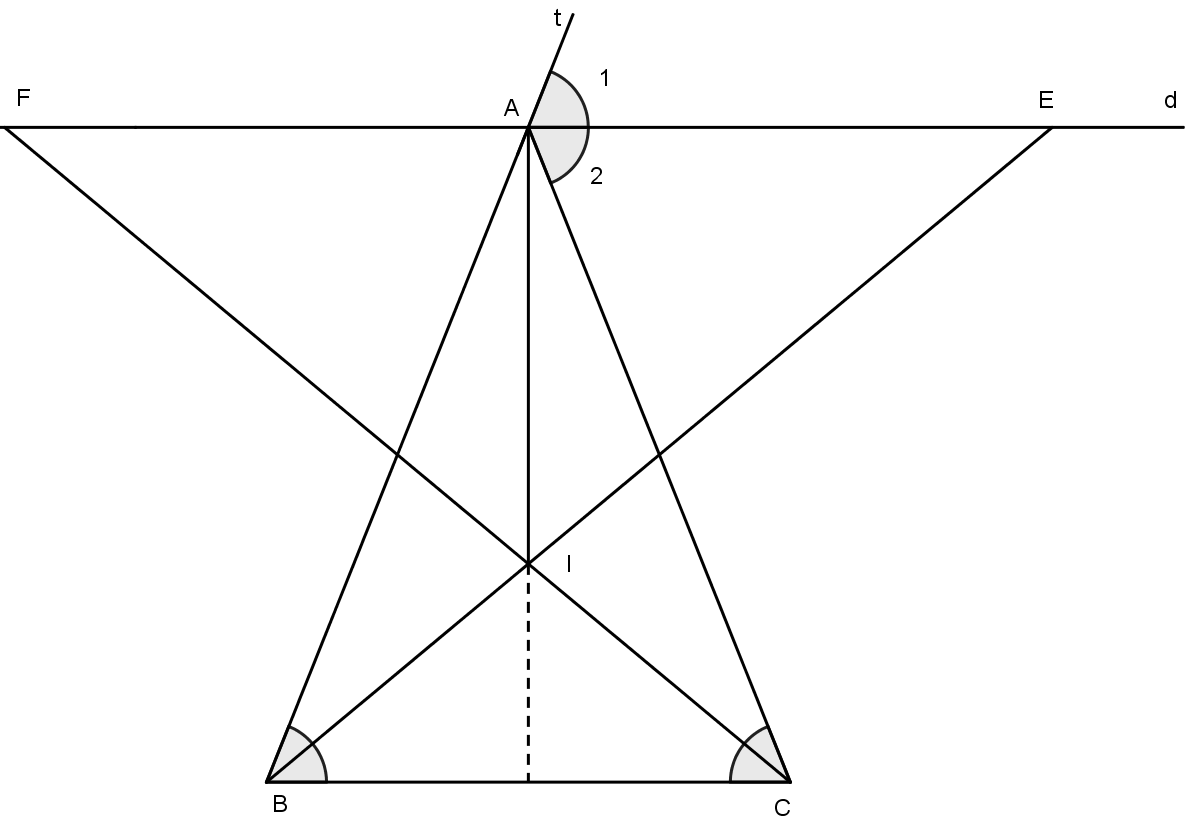
a)

\(\widehat {{A_1}} = \widehat B\) (d // BC, đồng vị)

\(\widehat B = \widehat C\)(\(\Delta ABC\) cân)

Nên \(\widehat {{A_1}} = \widehat C\)

Mà \(\widehat {{A_2}} = \widehat C\) (d // BC, so le)

Suy ra \(\widehat {{A_1}} = \widehat {{A_2}}\)

Vậy d là phân giác ngoài của \(\widehat {A\,}\)

b)

Ta có: \(\widehat {FEB} = \widehat {EBC} = \frac{1}{2}\widehat B\) (so le trong)

\(\widehat {FEC} = \widehat {FCB} = \frac{1}{2}\widehat C\) (so le trong)

Mà \(\widehat B = \widehat C\) (\(\Delta ABC\) cân)

Nên \(\widehat {FEB} = \widehat {EFC}\)

Suy ra \(\Delta IFE\) cân tại I

Mặt khác \(AI \bot AE.\)

Nên IA là đường cao của tam giác cân  IFE nên cũng là  đường trung tuyến.

Vậy AE =AF.

Câu 2: Gọi D là điểm nằm trên cạnh AB của tam giác vuông cân ABC \((\widehat A = {90^0})\). Trên tia đối của tia AC lấy E sao cho AE = AD. Chứng minh rằng CD vuông với BE.

Hướng dẫn giải

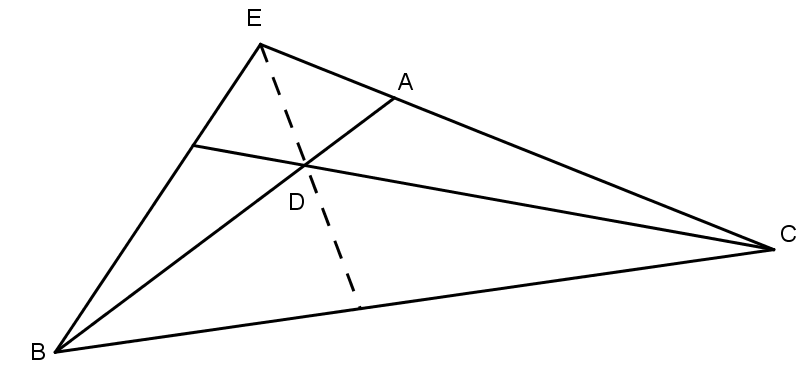
Ta có \(\Delta ADE\) vuông cân tại A nên \(\widehat {AED} = {45^0}\) mà \(\widehat {ACB} = {45^0}\) (\(\Delta ABC\) vuông cân tại A)

Do đó \(ED \bot BC\)

Ta lại có \(BA \bot EC.\)

Vậy D là trực tâm của \(\Delta EBC\)

Suy ra \(CD \bot BE\)

3. Luyện tập

3.1. Bài tập tự luận

Câu 1: Cho bốn điểm phân  biệt A, B, C, D trên mặt phẳng. Biết rằng AB vuông góc với AD, AC vuông góc với BD. Chứng minh rằng AD vuông góc với BC.

Câu 2: Cho hai đường thẳng x’x và yy’ cắt nhau tại O. Trên Ox, Ox’ lần lượt lấy các điểm B, D sao cho OA = OB, OC = OD.

Gọi M, N lần lượt là trung điểm của AB, CD.

Chứng minh M, O, N thẳng hàng.

Câu 3: Cho đường thẳng x’x và một điểm O nằm trên đường thẳng ấy. Dựng tia Oy vuông góc với x’x. Trên tia Oy lấy hai điểm A và B nào đó sao cho nằm giữa O và B, trên tia Ox lấy một điểm C nào đó. Gọi D là hình chiếu của A trên đường thẳng BC.

a) Chứng tỏ rằng hai đường thẳng x’x và AD cắt nhau tại điểm E.

b) Chứng minh: \(AC \bot BE\)

c) Chứng minh rằng hai góc BAE và BCE bù nhau (tổng số đo hai góc bằng \({180^0}\))

3.2. Bài tập trắc nghiệm

Câu 1: Cho tam giác ABC nhọn, hai đường cao BD và CE. Trên tia đối của tia BD lấy điểm I sao cho BI = AC. Trên tia đối của tia CE lấy điểm K sao cho CK = AB. Chọn câu đúng 

A. AI > AK

B. AI < AK

C. AI = 2AK

D. AI = AK

Câu 2: Cho tam giác ABC cân tại A, trung tuyến AM. Biết BC = 24cm, AM = 5cm. Tính độ dài các cạnh AB và AC

A. AB = AC = 13cm

B. AB = AC = 14cm

C. AB = AC = 15cm

D. AB = AC = 16cm

Câu 3: Cho tam giác ABC, hai đường cao AM và BN cắt nhau tại H. Hãy chọn phát biểu đúng

A. H là trọng tâm của tam giác ABC

B. H là tâm đường tròn nội tiếp tam giác ABC

C. CH là đường cao của tam giác ABC

D. CH là đường trung trực của tam giác ABC

Câu 4: Cho tam giác ABC cân tại A có AM là đường trung tuyến khi đó

A. AM vuông góc BC

B. AM là đường trung trực của BC

C. AM là đường phân giác của góc BAC

D. Cả A, B, C đều đúng

Câu 5: Đường cao của tam giác đều cạnh a có bình phương độ dài là

A. \(\frac{{3{a^2}}}{4}\)

B. \(\frac{{{a^2}}}{4}\)

C. \(\frac{{3{a^2}}}{2}\)

D. \(\frac{{3a}}{2}\)

4. Kết luận

Qua bài học này, các em cần nắm được những nội dung sau:

• Định nghĩa được đường cao của tam giác.
• Nắm được tính chất ba đường cao trong tam giác 
• Biết tính chất về đường cao, trung tuyến, trung trực, phân giác của tam giác.
• Áp dụng giải được những bài toán liên quan.