Toán 7 Chương 2 Bài 5: Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc (g-c-g)
Elib đã biên soạn và tổng hợp để giới thiệu đến các em nội dung bài giảng Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc. Bài giảng giúp các em nắm vững lý thuyết bài học, kèm theo đó là những bài tập minh họa có hướng dẫn giải chi tiết sẽ giúp các em hiểu bài hơn. Mời các em cùng theo dõi.
Mục lục nội dung

Toán 7 Chương 2 Bài 5: Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc (g-c-g)
1. Tóm tắt lý thuyết
1.1. Chú ý khi vẽ tam giác biết một cạnh và hai góc kề
Để vẽ được tam giác ABC tổng các số đo của hai góc đã cho phải nhỏ hơn 18001800
1.2. Trường hợp bằng nhau góc – cạnh – góc
Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
Nếu ΔABC và ΔA′B′C′ có
ˆB=^B′BC=B′C′ˆC=^C′
Thì ΔABC=ΔA′B′C′(c.g.c)
1.3. Hệ quả
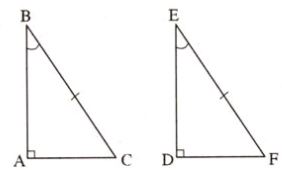
Hệ quả 1: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì tam giác vuông đó bằng nhau.
Hệ quả 2: Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì tam giác vuông đó bằng nhau.
2. Bài tập minh họa
Câu 1: Cho ΔABC có ˆB=ˆC
Tia phân giác của góc B cắt AC ở D. Tia phân giác của góc C cắt AB ở E. So sánh độ dài các đoạn thẳng BD và CE.
Hướng dẫn giải
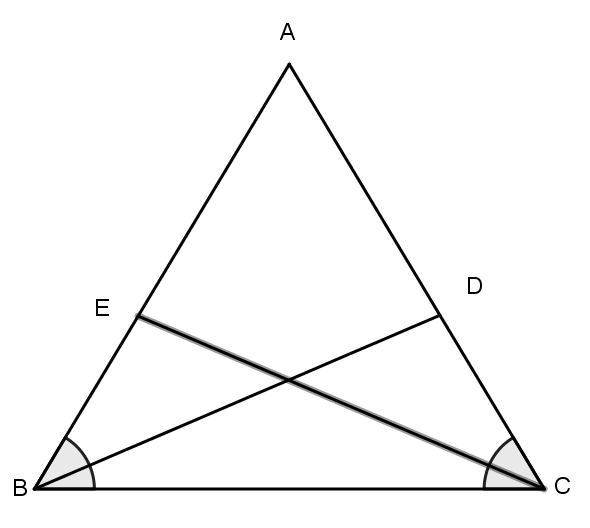
ΔEBC và ΔDCB có:
^EBC=^DCB (gt ˆB=ˆC)
BC cạnh chung
^ECB=^DBC(gt=12ˆB=12ˆC)
Nên ΔEBC=ΔDCB (c.g.c)
Suy ra CE = BD.
Câu 2: Cho tam giác ABC có AB = AC và ˆB=ˆC. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD = AE. Gọi I là giao điểm của BE và CD. Chứng minh rằng: ΔIBD=ΔICE.
Hướng dẫn giải
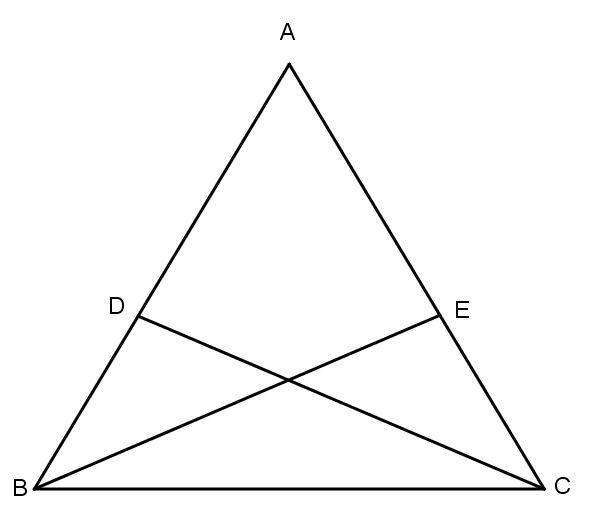
Xét hai tam giác ABE và ACB chúng có:
AB = AC (giả thiết)
ˆA chung
AD = AE (giả thiết)
Nên ΔABE=ΔACD(c.g.c)
Suy ra BE = CD và ^ABE=^ACD(1)
Ta có AB = AC và AD = AE (giả thiết)
Nên BD = CE
ˆB=ˆC (giả thiết) (2)
BC chung
Do đó ΔBCD=ΔCBE
Suy ra ^BCD=^CEB(3)
Từ (1), (2), (3) ta có:
ΔIBD=ΔICE(g.c.g)
Câu 3: Cho tam giác ABC. Trên cạnh BC lấy cac điểm D và E sao BD = CE. Qua D và E kẻ các đường thẳng song song với AB cắt cạnh AC theo thứ tự I và K.
Chứng minh rằng: DI + EK = AB
Hướng dẫn giải
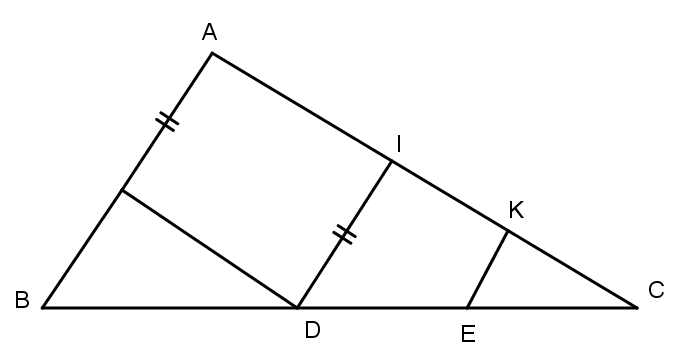
Qua D vẽ đường thẳng song song với AC cắt AB tại L.
Xét hai tam giác BDL và ECK có:
B1=E1 (cặp góc đồng vị do EK//AB)
BD=CE (giả thiết)
D1=C (cặp góc đồng vị do DK // CA)
⇒ΔBDL=ΔECK (g.c.g)
⇒BL=EK(1)
Mặt khác ta có:
AL = DI (theo bài 350) (2)
Mà AB=AL+LB(3)
Từ (1), (2) và (3) suy ra: AB = DI + EK
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Cho tam giác ABC (AB=AC) và I là trung điểm của cạnh đáy BC. Dựng tia Cx song song với tia BA sao cho hai tia BA và Cx nằm trong hai nửa mặt phẳng đối nhau có bờ là đường thẳng BC. Lấy một điểm D nào đó trên AB. Gọi E là một điểm trên tia Cx sao cho BD = CE. Chứng minh rằng: Ba điểm D, I, E thẳng hàng.
Câu 2: Cho tam giác ABC biết AB =3cm, BC=5cm và CA=4cm. Gọi đường thẳng qua A và song song với BC là a, đường thẳng qua B và song song với CA là b và đường thẳng C vào song song với AD là c. Gọi A’, B’, C’ theo thứ tự là giao điểm của các đường thẳng b và c, a và c,a và b. Tìm độ dài các cạnh của tam giác A’B’C’.
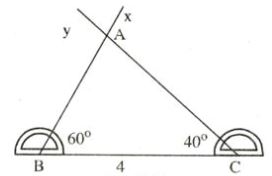
Câu 3: Tam giác ABC có ˆA=600, các tia phân giác BM và CN cắt nhau ở I. Biết rằng BC=4m. Tính tổng BN=CM.
3.2. Bài tập trắc nghiệm
Câu 1: Cho tam giác ABC và tam giác NPM có BC = PM, ˆB=ˆP. Cần thêm một điều kiện gì để tam giác MPN và tam giác CBA bằng nhau theo trường hợp góc - cạnh - góc?
A. ˆM=ˆA
B. ˆA=ˆP
C. ˆC=ˆM
D. ˆA=ˆN
Câu 2: Cho tam giác ABC và tam giác MNP có ˆA=ˆM,ˆB=ˆN. Cần thêm điều kiện gì để tam giác ABC và tam giác MNP bằng nhau theo trường hợp góc - cạnh - góc
A. AC = MP
B. AB = MN
C. BC = NP
D. AC = MN
Câu 3: Cho tam giác ABC và tam giác MNP có ˆB=ˆN=900, AC = MP, ˆC=ˆM. Phát biểu nào trong các phát biểu sau đây là đúng
A. ΔABC=ΔPMN
B. ΔACB=ΔPNM
C. ΔBAC=ΔPNM
D. ΔABC=ΔPNM
Câu 4: Cho góc nhọn xOy, Oz là tia phân giác của góc đó. Qua điểm A thuộc tia Ox kẻ đường thẳng song song với Oy cắt Oz ở M. Qua M kẻ đường thẳng song song với Ox cắt Oy ở B. Chọn câu đúng
A. OA > OB, MA > MB
B. OA = OB, MA = MB
C. OA < OB, MA < MB
D. OA < OB, MA = MB
Câu 5: Cho đoạn thẳng AB, O là trung điểm của AB. Trên cùng một nửa mặt phẳng bờ AB vẽ các tia Ax, By vuông góc với AB. Gọi C là điểm thuộc tia Ax. Đường vuông góc với OC tại O cắt tia By ở D. Khi đó
A. AC = CD - BD
B. AC = DC + BD
C. CD = AC - BD
D. CD = AC + BD
4. Kết luận
Qua bài học này, các em cần nắm được những nội dung sau:
-
Chú ý khi vẽ tam giác biết một cạnh và hai góc kề.
-
Trường hợp bằng nhau góc - cạnh - góc của tam giác và hệ quả.
-
Vận dụng lý kiến thức làm được các bài toán liên quan.
Tham khảo thêm
- doc Toán 7 Chương 2 Bài 1: Tổng ba góc của một tam giác
- doc Toán 7 Chương 2 Bài 2: Hai tam giác bằng nhau
- doc Toán 7 Chương 2 Bài 3: Trường hợp bằng nhau thứ nhất của tam giác cạnh - cạnh - cạnh (c-c-c)
- doc Toán 7 Chương 2 Bài 4: Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh (c-g-c)
- doc Toán 7 Chương 2 Bài 6: Tam giác cân
- doc Toán 7 Chương 2 Bài 7: Định lí Py-ta-go
- doc Toán 7 Chương 2 Bài 8: Các trường hợp bằng nhau của tam giác vuông