Toán 7 Chương 2 Bài 7: Đồ thị của hàm số y = ax (a ≠ 0)
Sau đây mời các em học sinh lớp 7 cùng tìm hiểu về bài Đồ thị của hàm số y = ax (a ≠ 0). Bài giảng dưới đây đã được eLib biên soạn khái quát lý thuyết cần nhớ, đồng thời có các bài tập được tổng hợp đầy đủ các dạng toán liên quan giúp các em dễ dàng nắm được kiến thức trọng tâm của bài.
Mục lục nội dung

Toán 7 Chương 2 Bài 7: Đồ thị của hàm số y = ax (a ≠ 0)
1. Lý thuyết
1.1. Đồ thị của hàm số
Đồ thị của hàm số là tập hợp tất cả các điểm biểu diễn các cặp giá trị tương ứng (x;y) trên mặt phẳng toạ độ.
1.2. Đồ thị của hàm số
- Đồ thị của hàm số là một đường thẳng đi qua gốc toạ độ.
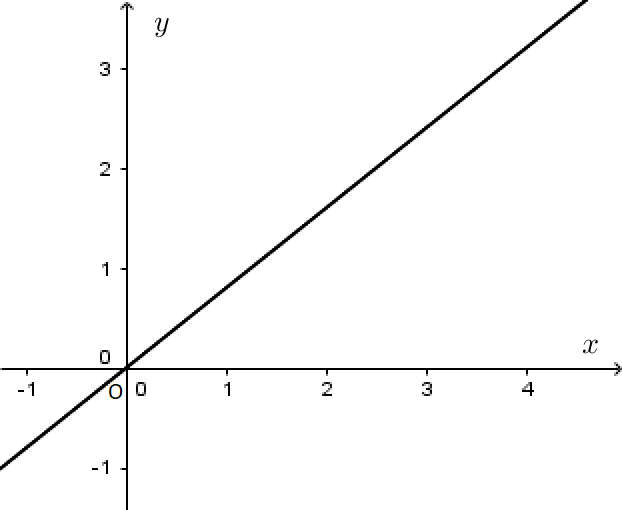
a>0
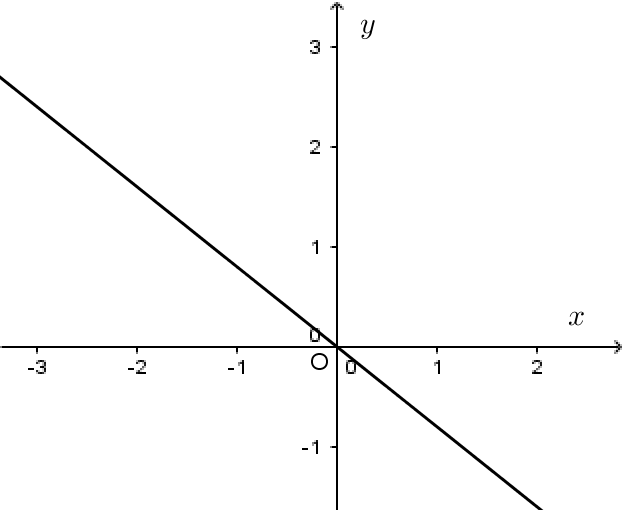
a<0
- Vì đồ thị của hàm số y = ax là một đường thẳng đi qua gốc toạ độ nên ta chỉ cần xác định thêm một điểm A (thường cho x=1; y=a) khác điểm gốc O. Vẽ đường thẳng OA ta được đồ thị của hàm số y = ax.
2. Bài tập minh họa
Câu 1: Xác định hệ số a của hàm số y = ax trong mỗi trường hợp sau:
a. Đồ thị của hàm số đi qua điểm A(1;3).
b. Đồ thị của hàm số đi qua điểm B(-2;1).
Cho biết hàm số trong mỗi trường hợp trên đi qua góc phần tư nào của hệ trục toạ độ, tại sao?
Hướng dẫn giải
a. Hàm số đi qua điểm A(1;3) nên ta có:
Vậy .
b. Tương tự hàm số đi qua điểm B(-2; 1), ta có:
Vậy .
Đồ thị hàm số y=3x qua góc phần tư I và III (vì hai toạ độ cùng dấu (cùng dương, cùng âm)).
Đồ thị hàm số qua góc phần tư II và IV (vì hai toạ độ trái dấu).
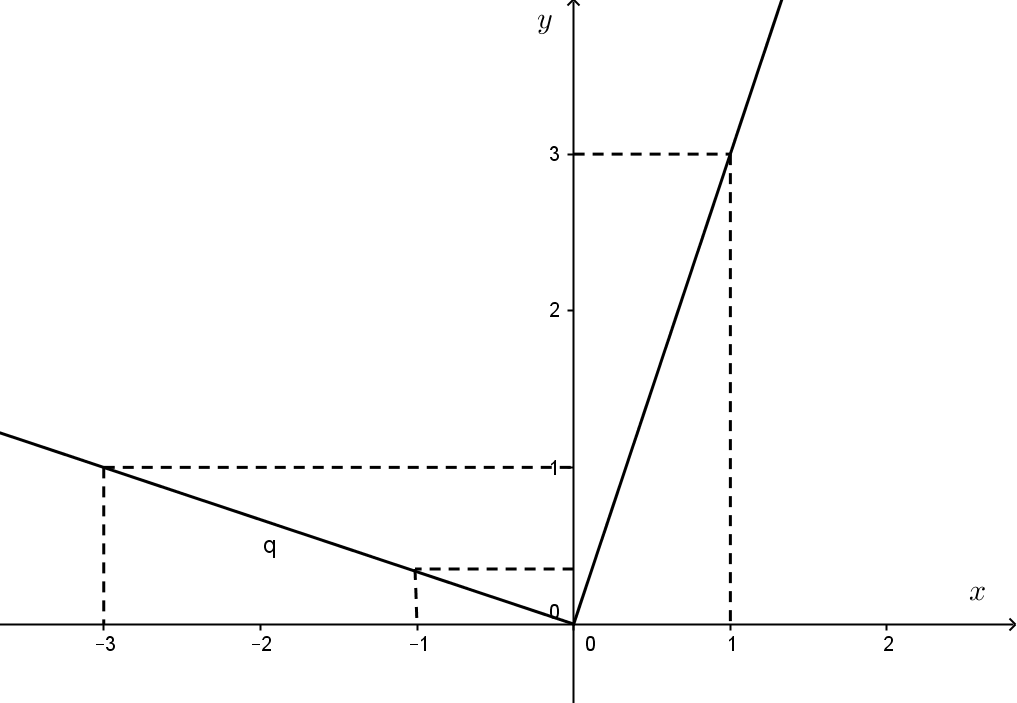
Câu 2: Vẽ đồ thị của hàm số
Hướng dẫn giải
-
Với :
Cho x = 0 được thuộc đồ thị
Cho x = 1 được thuộc đồ thị
-
Với :
Cho được thuộc đồ thị
Cho được thuộc đồ thị
Vẽ đồ thị: Nối A, O,B, C ta được đồ thị là đường gấp khúc AOC.
3. Luyện tập
3.1. Bài tập tự luận
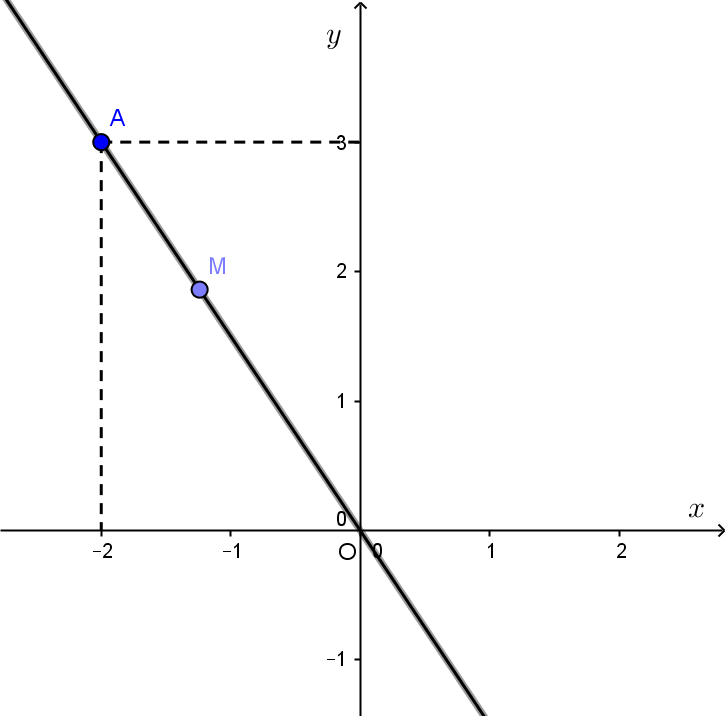
Câu 1: Cho hình vẽ bên, điểm M có tọa độ với Hãy tính tỉ số
Câu 2:
a. Vẽ đồ thị hàm số .
b. Gọi A là điểm trên đồ thị. Tìm toạ độ điểm A, biết
c. Gọi B là điểm trên đồ thị. Tìm toạ độ điểm B biết .
Câu 3: Cho hàm số y=f(x) thoả mãn:
a. f(0)=0.
b. với .
Chứng minh rằng f(x)=ax với a là hằng số.
3.2. Bài tập trắc nghiệm
Câu 1: Điểm thuộc đồ thị hàm số y = -2x là:
A. M(-2; -2).
B. N(1; 4).
C. P(-1; -2).
D. Q(-1; 2).
Câu 2: Đồ thị hàm số y = -5x không đi qua điểm
A. M(1; 5).
B. N(-2; 10).
C. P(-1; 5).
D. Q(-2; 10).
Câu 3: Đồ thị hàm số là đường thẳng OA với O(0;0) và
A. A(1; 5).
B. A(-1; -5).
C. A(5; 1).
D. A(-5; 1).
Câu 4: Cho hàm số y = 5x. Trong các điểm A(1; 2), B(2; 10), C(-2; 10), D(-1/5; -1) có bao nhiêu điểm thuộc đồ thị hàm số y = 5x
A. 2.
B. 1.
C. 3.
D. 4.
Câu 5: Cho hàm số y = (2m+1)x. Xác định m biết đồ thị hàm số đi qua điểm A(-1; 1)
A. m = 1.
B. m = -1.
C. m = 0.
D. m = 2.
Câu 6: Cho ba điểm A(-1; 4), B(2; -8), C(1,5; -6). Chọn câu đúng:
A. Ba điểm A(-1; 4), B(2; -8), C(1,5; -6) đều nằm trên trục hoành.
B. Ba điểm A(-1; 4), B(2; -8), C(1,5; -6) đều nằm trên trục tung.
C. Ba điểm A(-1; 4), B(2; -8), C(1,5; -6) không thẳng hàng.
D. Ba điểm A(-1; 4), B(2; -8), C(1,5; -6) thẳng hàng.
4. Kết luận
Qua bài học này, các em cần nắm được những nội dung sau:
- Khái niệm đồ thị hàm số, dạng đồ thị hàm số y = ax (a ≠ 0).
- Cách vẽ đồ thị hàm số y = ax (a ≠ 0) và vẽ thành thạo nó.
Tham khảo thêm
- doc Toán 7 Chương 2 Bài 1: Đại lượng tỉ tệ thuận
- doc Toán 7 Chương 2 Bài 2: Một số bài toán về đại lượng tỉ lệ thuận
- doc Toán 7 Chương 2 Bài 3: Đại lượng tỉ lệ nghịch
- doc Toán 7 Chương 2 Bài 4: Một số bài toán về đại lượng tỉ lệ nghịch
- doc Toán 7 Chương 2 Bài 5: Hàm số
- doc Toán 7 Chương 2 Bài 6: Mặt phẳng tọa độ