Toán 7 Chương 1 Bài 6: Từ vuông góc đến song song
Elib đã biên soạn và tổng hợp để giới thiệu đến các em nội dung bài giảng Từ vuông góc đến song song. Bài giảng giúp các em nắm vững lý thuyết bài học, kèm theo đó là những bài tập minh họa có hướng dẫn giải chi tiết sẽ giúp các em hiểu bài hơn. Mời các em cùng theo dõi.
Mục lục nội dung

Toán 7 Chương 1 Bài 6: Từ vuông góc đến song song
1. Tóm tắt lý thuyết
1.1. Quan hệ giữa tính vuông góc với tính song song của ba đường thẳng
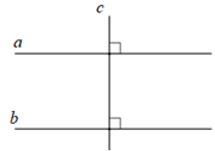
- Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
Ví dụ: Ta có: {a⊥cb⊥c⇒a//b
- Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.
Ví dụ: Ta có: {a//bc⊥a⇒c⊥b
1.2. Ba đường thẳng song song
- Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau.
- Ba đường thẳng d, d’, d’’ song song với nhau từng đôi mội ta nói ba đường thẳng ấy song song với nhau. Ký hiệu: d // d’ // d’’.
2. Bài tập minh họa
Câu 1: Trong hình, biết ˆM=1200,ˆN=600 và ˆF=900. Chứng minh a⊥c.
Hướng dẫn giải
Ta có: ˆM+ˆN=1200+600=1800, suy ra a//b (vì có cặp góc trong cùng phía bù nhau).
Ta có ˆF=900⇒c⊥b, mà a // b nên c⊥a(hệ quả của định lý hai đường thẳng song song).
Câu 2: Cho góc Trên tia Ox lấy điểm A. Qua A vẽ tia Az sao cho tia Az và Oy nằm trên cùng một nửa mặt phẳng bờ chừa tia Ox và ^OAz=350.
a. Chứng minh: Az // Oy
b. Vẽ tia Az’ đối với tia Az. Chứng minh hai đường phân giác của hai góc xOy và OAz’ song song với nhau.
Hướng dẫn giải
a. Ta có:
^xOy=1450(gt)^OAz=350(gt)⇒^xOy+^OAz=1800
mà ^xOy và ^OAz ở vị trí góc trong cùng phía nên Az // Oy.
b. Gọi Ot phân giác ^AOy nên
^AOt=12^AOy=12.1450=72030′(1)
^OAz′^OAz kề bù mà ^OAz=350 nên ^OAz′=1450
Gọi Am là phân giác ^OAz′ ta có: ^OAm=12^OAz′=72030′(2)
Từ (1) và (2) suy ra ^OAm=^AOt.
^OAm
Mà và ^AOt ở vị trí so le trong
Nên Am // Ot.
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Cho góc nhọn xOy. QR⊥Ox.Từ điểm M trên cạnh Ox, dựng MN⊥Oy; dựng NP⊥Ox; dựng
a. Chứng minh MN // PQ; NP // QR.
b. Tìm góc bằng góc PMN.
c. Chứng minh ^MNP=^NPQ=^PQR;^PNQ=^RQO;^QPR=^NMP.
Câu 2: Cho ^xOy=α, điểm A nằm trên Oy. Qua A vẽ tia Am. Tính số đo góc ^OAm để Am//Ox.
3.2. Bài tập trắc nghiệm
Câu 1: Cho ba đường thẳng phân biệt a, b và c, biết a // b và a ⊥ c. Kết luận nào sau đây đúng?
A. b // c
B. b ⊥ c
C. a ⊥ b
D. Tất cả các đáp án trên đều sai
Câu 2: Chọn câu sai:
Cho bốn đường thẳng phân biệt m, n, p và q. Biết m vuông góc với n, n vuông góc với p và p vuông góc với q. Khi đó:
A. m // p
B. n // q
C. p // n
D. m vuông góc q
Câu 3: Cho hai đường thẳng a và b cùng vuông góc với đường thẳng c, c vuông góc với a tại M và vuông góc với b tại N. Một đường thẳng m cắt a, b tại A, B. Biết ^ABN−^MAB=40o. Số đo góc BAM là
A. 80o
B. 70o
C. 75o
D. 108o
Câu 4: Điền tiếp vào chỗ '' ... '' để có được một định lý.
''Cho ba đường thẳng phân biệt, nếu một đường thẳng song song với một trong hai đường thẳng thì nó ...''
A. song song với đường thẳng còn lại
B. cắt đường thẳng còn lại
C. vuông góc với đường thẳng còn lại
D. trùng với đường thẳng còn lại
Câu 5: Khẳng định nào sau đây là sai?
A. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
B. Cho hai đường thẳng a và b song song với nhau, nếu đường thẳng c cắt a thì đường thẳng c cũng cắt b.
C. Nếu hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau.
D. Có duy nhất một đường thẳng song song với một đường thẳng cho trước.
4. Kết luận
Qua bài học này, các em cần nắm được những nội dung sau:
-
Quan hệ giữa tính vuông góc với tính song song của ba đường thẳng.
-
Ba đường thẳng song song.
Tham khảo thêm
- doc Toán 7 Chương 1 Bài 1: Hai góc đối đỉnh
- doc Toán 7 Chương 1 Bài 2: Hai đường thẳng vuông góc
- doc Toán 7 Chương 1 Bài 3: Các góc tạo bởi một đường thẳng cắt hai đường thẳng
- doc Toán 7 Chương 1 Bài 4: Hai đường thẳng song song
- doc Toán 7 Chương 1 Bài 5: Tiên đề Ơ-clit về đường thẳng song song
- doc Toán 7 Chương 1 Bài 7: Định lí
.JPG)
.JPG)
.JPG)

