Toán 7 Chương 2 Bài 4: Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh (c-g-c)
Mời các em cùng tham khảo nội dung bài giảng Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh do eLib biên soạn và tổng hợp dưới đây. Bài giảng giúp các em nắm vững lý thuyết bài học, thêm vào đó là những bài tập minh họa có hướng dẫn giải chi tiết sẽ giúp các em dễ dàng làm được các dạng bài tập ở phần này.
Mục lục nội dung

Toán 7 Chương 2 Bài 4: Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh (c-g-c)
1. Tóm tắt lý thuyết
1.1. Chú ý khi vẽ tam giác biết hai cạnh và góc xen giữa
Để vẽ được tam giác ABC, số đo của góc đã cho phải nhỏ hơn 1800
1.2. Trường hợp bằng nhau cạnh – góc – cạnh
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì tam giác đó bằng nhau.
Nếu ΔABC và ΔA′B′C′ có
AB=A′B′
ˆB=^B′
BC=B′C′
Thì ΔABC=ΔA′B′C′(c.g.c)
1.3. Hệ quả
Nếu hai cạnh góc vuông của tam giác này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
2. Bài tập minh họa
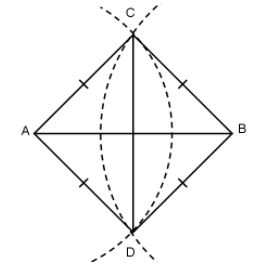
Câu 1: Cho đoạn thẳng AB. Vẽ các cung tâm A và tâm B có cùng bán kính sao cho chúng cắt nhau tại C và D. Chứng minh:
a. CD là tia phân giác của góc ACB.
b. CD là đường trung trực của AB.
Hướng dẫn giải
a. ΔACD và ΔBCD có
AC = BC (=bán kính)
AC = BD (=bán kính)
CD cạnh chung
Do đó ΔACD=ΔBCD(c.c.c)
Suy ra ^ACD=^BCD
Vậy CD là tia phân giác của góc C.
b. Gọi H là giao điểm của CD và AB
ΔACH và ΔBCH có:
AC = BC (gt)
^ACH=^BCH(ΔACD=ΔBCD)
CH cạnh chung
Nên ΔACH=ΔBCH(c.g.c)
Suy ra HA=HB,^H1=^H2
Ta lại có ^H1+^H2=1800 nên ^H1+^H2=900, do đó CH⊥AB và HA = HB nên CH là đường trung trực của AB.
Vậy CD là đường trung trực của AB.
Câu 2: Cho đoạn thẳng AB. Gọi A là một điểm trên đường trung trực xy của đường thẳng AB và M là giao điểm của xy với AB. Chứng minh AB = AC.
Hướng dẫn giải
Xét hai tam giác AMB và AMC
Ta có:
MB=MC(gt)^AMB=^AMC=900(AM⊥BC)
AH cạnh chung
Nên ΔAMB=ΔAMC(c.g.c)
Nên ΔAMB=ΔAMC(c.g.c)
Suy ra AB = AC.
Câu 3: Cho góc xOy với điểm I trên tia phân giác Oz, lấy A trên Ox, B trên Oy sao cho OA = OB.
a. Chứng minh rằng ΔAOI=ΔBOI.
b. Đoạn thẳng AB cắt Oz tại H chứng minh rằng ΔAIH=ΔBIH
c. Chứng minh rằng các tam giác AIH và BIH đều là tam giác vuông.
Hướng dẫn giải
a. Hai tam giác AOI và BOI có: IO chung, OA = OB (gt)
^AOI=^BOI (Oz là tia phân giác)
Vậy ΔAOI=ΔBOI(c.g.c)
b. Do ΔAOI=ΔBOI, suy ra
IA = IB (1)
^AOI=^BOI
Nhưng ^AIH kề bù với AIO, ^BIH kề bù với ^BOI
Suy ra ^AIH=^BIH(2)
IH cạnh chung (3)
Từ (1), (2), (3) suy ra ^AIH=^BIH(c.g.c)
c. Do ΔAIH=ΔBIH⇒^AHI=^BHI
Vì ^AHI=^BHI và lại là góc kề bù
Suy ra ^AHI=^BHI=18002=900
Vậy ΔAIH là tam giác vuông tại H
ΔBIH là tam giác vuông tại H.
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Cho đường thẳng AB, trên hai nữa mặt phẳng đối phẳng đối nhau bờ là là đường thẳng chứa đoạn AB vẽ hai tia Ax⊥AB,By⊥BA. Trên Ax và By lần lượt lấy hai điểm C và D sao cho AC = BD. Gọi O là trung điểm AB.
a. Chứng minh ΔAOC=ΔBOD
b. Chứng min O là trung điểm CD.
Câu 2: Cho bốn tia Ox, Oy, Oz, Ot theo thứ tự sao cho ^xOy=^yOt. Trên Ox, Oz lấy hai điểm A và C sao cho OA=OC, trên Oy và Ot lấy hai điểm B và D sao cho OB=OD. Chứng minh ^OAB=^OCD.
Câu 3: Cho góc xOy, trên Ox lấy các điểm A, B và trên Oy lấy các điểm C, D sao cho OA=OC; AB = CD. Chứng minh rằng:
a. ΔABC=ΔCDA
b. ΔABD=ΔCDB
3.2. Bài tập trắc nghiệm
Câu 1: Cho tam giác ABC vuông tại A, tia phân giác BD của góc B (D thuộc AC). Trên cạnh BC lấy điểm E sao cho BE = BA. Hai góc nào sau đây bằng nhau?
A. ^EDC=^BAC
B. ^EDC=^ACB
C. ^EDC=^ABC
D. ^EDC=^ECD
Câu 2: Cho tam giác BAC và tam giác KEF có BA = EK, ˆA=ˆK, CA = KF. Phát biểu nào trong các phát biểu sau đây là đúng?
A. ΔBAC=ΔEKF
B. ΔBAC=ΔEFK
C. ΔABC=ΔEKF
D. ΔBAC=ΔKEF
Câu 3: Cho hai đoạn thẳng BD và EC vuông góc với nhau tại A sao cho AB = AE, AD = AC, AB < AC. Phát biểu nào trong các phát biểu sau đây là sai:
A. ΔAED=ΔABC
B. BC = ED
C. EB = CD
D. ^ABC=^AED
Câu 4: Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C, trên tia Oy lấy hai điểm B, D sao cho OA = OB, OC = OD (A nằm giữa O và C, B nằm giữa O và D). Chọn câu đúng
A. ΔOAD=ΔBOC
B. ΔOAD=ΔOCB
C. ΔAOD=ΔOBC
D. ΔOAD=ΔOBC
Câu 5: Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C, trên tia Oy lấy hai điểm B, D sao cho OA = OB, OC = OD (A nằm giữa O và C, B nằm giữa O và D). So sánh ^CAD và ^CBD
A. ^CAD=^CBD
B. ^CAD<^CBD
C. ^CAD>^CBD
D. ^CAD=2.^CBD
4. Kết luận
Qua bài học này, các em cần nắm được những nội dung sau:
-
Chú ý khi vẽ tam giác biết hai cạnh và góc xen giữa.
-
Trường hợp bằng nhau cạnh - góc - cạnh của tam giác và hệ quả.
-
Vận dụng lý kiến thức làm được các bài toán liên quan.
Tham khảo thêm
- doc Toán 7 Chương 2 Bài 1: Tổng ba góc của một tam giác
- doc Toán 7 Chương 2 Bài 2: Hai tam giác bằng nhau
- doc Toán 7 Chương 2 Bài 3: Trường hợp bằng nhau thứ nhất của tam giác cạnh - cạnh - cạnh (c-c-c)
- doc Toán 7 Chương 2 Bài 5: Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc (g-c-g)
- doc Toán 7 Chương 2 Bài 6: Tam giác cân
- doc Toán 7 Chương 2 Bài 7: Định lí Py-ta-go
- doc Toán 7 Chương 2 Bài 8: Các trường hợp bằng nhau của tam giác vuông
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)

