Toán 7 Chương 1 Bài 7: Định lí
Mời các em cùng tham khảo nội dung bài giảng Định lí do eLib biên soạn và tổng hợp dưới đây. Bài giảng giúp các em nắm vững lý thuyết bài học, thêm vào đó là những bài tập minh họa có hướng dẫn giải chi tiết sẽ giúp các em dễ dàng làm được các dạng bài tập ở phần này.
Mục lục nội dung

Toán 7 Chương 1 Bài 7: Định lí
1. Tóm tắt lý thuyết
1.1. Định lý
- Định lý là khẳng định suy ra từ những khẳng định được coi là đúng.
- Mỗi định lý thường được phát biểu dưới dạng “Nếu A thì B”.
-+ A gọi là giả thiết.
+ B gọi là kết luận.
- Giả thiết và kết luận được viết tắt tương ứng là GK và KL.
1.2. Chứng minh định lý
- Chứng minh định lý là dùng lập luận để từ giả thiết suy ra kết luận.
- Để chứng minh định lý ta làm như sau:
+ Vẽ hình.
+ Ghi giả thiết, kết luận.
+ Nêu các bước chứng minh. Mỗi bước gồm một khẳng định và căn cứ của khẳng định đó.
2. Bài tập minh họa
Câu 1: Điền vào chỗ trống bằng những nội dung thích hợp để được các định lý:
a. Nếu M là trung điểm của đoạn AB thì….
b. Nếu …. thì MA=MB=12AB.MA=MB=12AB.
c. Nếu tia Ot là tia phân giác của góc xOy thì ….
d. Nếu …..thì ^xOt=^tOy=12^xOyˆxOt=ˆtOy=12ˆxOy
e. Nếu ^xOyˆxOy và ^x′Oy′ là hai góc đối đỉnh thì …..
Hướng dẫn giải
a. Có thể điền vào chỗ trống theo vài cách sau đây:
M nằm giữa A và B.
MA= MB.
MA=MB=12AB.
M nằm giữa A,B và MA = MB.
MA + MB = AB và MA = MB.
b. Chỉ có một cách điền vào chỗ trống: M là trung điểm của đoạn AB.
c. Có thể điền vào chỗ trống theo vài cách sau đây:
Ot nằm giữa hai tia Ox và Oy.
^xOt=^tOy.
^xOt=^tOy=12^xOy.
Ot nằm giữa hai tia Ox, Oy và ^xOy=^tOy.
^xOy=^tOy và ^xOt+^tOy+^tOy=^xOy.
d. Chỉ có một cách điền vào chỗ trống: Ot là tia phân giác của góc xOy.
e. Có thể điền như sau: Chúng bằng nhau.
Nhận xét: Ở câu a, c, e còn có thể điền theo nội dung khác.
Câu 2: Cho mệnh đề: “Số đo của góc tạo bởi tia phân giác với mỗi cạnh của góc bằng nửa số đo của góc ấy”.
a. Phát biểu mệnh đề trên dưới dạng: “Nếu…. thì….”
b. Hãy chứng minh mệnh đề đó.
Hướng dẫn giải
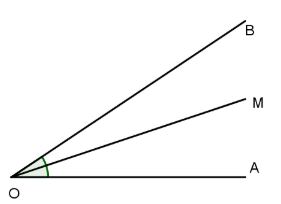
a. Nếu OM là tia phân giác của góc AOB thì:
^AOM=^MOB=12^AOB.
b. Chứng minh OM là phân giác của góc AOB nên:
^MOA+^MOB=^AOB^MOA=^MOB}2^MOA=^APB⇒^MOA=12^AOB.
Mà ^MOA=^MOB nên ^MOA=^MOB=12^AOB.
Câu 3: Cho mệnh đề sau: “C là một điểm nằm trên đoạn thẳng AB. Gọi M là trung điểm của đoạn AC, N là trung điểm của đoạn BC thế thì MN=12AB. Hãy chứng minh.
Hướng dẫn giải
Ta có M là trung điểm của đoạn AC nên M thuộc tia AC, tương tự N thuộc tia BC.
Hai tia CA, CB là hai tia đối nhau (do C nằm giữa AB) ⇒ C nằm giữa M và N ( Hình bên)
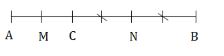
Lại có: MC=12ACNC=12BC}⇒MC+NC=12AC+12BC=12(AC+BC)=12AB.
Hay MN=12AB.
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Chứng minh định lý: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông”.
Câu 2: Chứng minh định lý sau: Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau.
Câu 3:
a. Hãy phát biểu định lý sau dưới dạng “nếu…thì…”: “Số đo góc tạo bởi tia phân giác với mỗi cạnh của góc bằng nửa số đo góc ấy”.
b. Chứng minh định lý đó.
3.2. Bài tập trắc nghiệm
Câu 1: Chứng minh định lí là:
A. Dùng lập luận để từ giả thiết suy ra kết luận.
B. Dùng hình vẽ để từ giả thiết suy ra kết luận.
C. Dùng đo đạc thực tế để từ giả thiết suy ra kết luận.
D. Cả A, B, C đều sai.
Câu 2: Khi chứng minh một định lý, người ta cần:
A. Chứng minh định lý đó đúng trong một trường hợp cụ thể của giả thiết.
B. Chứng minh định lý đó đúng trong hai trường hợp cụ thể của giả thiết.
C. Chứng minh định lý đó đúng trong mọi trường hợp có thể xảy ra của giả thiết.
D. Chứng minh định lý đó đúng trong vài trường hợp cụ thể của giả thiết.
Câu 3: Trong các câu sau, câu nào cho một định lí:
A. Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
B. Đường thẳng nào vuông góc với một trong hai đường thẳng cắt nhau thì song song với đường thẳng kia.
C. Nếu hai đường thẳng AB và AC cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song.
D. Nếu hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì hai đường thẳng đó song song.
Câu 4: Cho định lí: "Nếu hai đường thẳng song song cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau:. Gỉa thiết của định lí là:
.jpg)
A. a//b,a⊥c.
B. a//b,c∩a={A},c∩b={B}.
C. a //b, a // c.
D. a // b, c bất kì.
Câu 5: Trong định lý ''Hai góc đối đỉnh thì bằng nhau''.
Ta có giả thiết của định lý là:
A. a cắt b tại O.
B. góc O1 và góc O2 là hai góc đối đỉnh.
C. góc O1 và góc O2 là hai góc bằng nhau.
D. góc O1 và góc O2 là hai góc nhọn.
4. Kết luận
Qua bài học này, các em cần nắm được những nội dung sau:
- Hình thành khái niệm định lí.
- Cách chứng minh định lí.
- Chứng minh được một vài định lí đơn giản.
Tham khảo thêm
- doc Toán 7 Chương 1 Bài 1: Hai góc đối đỉnh
- doc Toán 7 Chương 1 Bài 2: Hai đường thẳng vuông góc
- doc Toán 7 Chương 1 Bài 3: Các góc tạo bởi một đường thẳng cắt hai đường thẳng
- doc Toán 7 Chương 1 Bài 4: Hai đường thẳng song song
- doc Toán 7 Chương 1 Bài 5: Tiên đề Ơ-clit về đường thẳng song song
- doc Toán 7 Chương 1 Bài 6: Từ vuông góc đến song song
.JPG)

