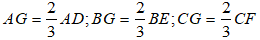Toán 7 Chương 3 Bài 4: Tính chất ba đường trung tuyến của tam giác
eLib xin giới thiệu đến các em nội dung bài giảng do eLib tổng hợp và biên soạn dưới đây. Bài học sẽ giúp các em tìm hiểu về Tính chất ba đường trung tuyến của tam giác cùng với những bài tập minh họa có hướng dẫn giải chi tiết sẽ giúp các em dễ dàng nắm đươc nội dung phần này.
Mục lục nội dung

Toán 7 Chương 3 Bài 4: Tính chất ba đường trung tuyến của tam giác
1. Tóm tắt lý thuyết
1.1. Đường trung tuyến của tam giác
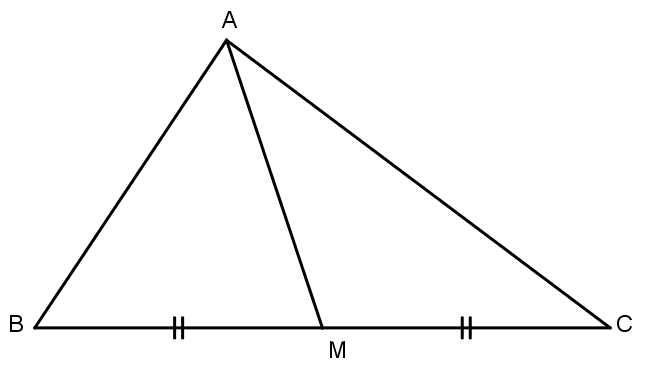
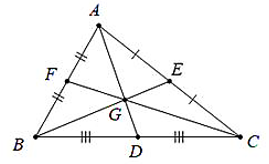
- Đoạn thẳng AM đối đỉnh A của tam giác ABC với trung điểm M của cạnh BC gọi là đường trung tuyến (xuất phát từ đỉnh A hoặc ứng với cạnh BC) của tam giác ABC.
- Đường thẳng AM cũng gọi là đường trung tuyến của tam giác ABC.
- Mỗi tam giác có ba đường trung tuyến
- Đường trung tuyến của một tam giác là đoạn thẳng nối đỉnh và trung điểm cạnh đối diện
1.2. Tính chất ba đường trung điểm của tam giác
Định lý: Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm đó cách mỗi đỉnh một khoảng bằng 23 độ dài trung tuyến đi qua đỉnh ấy.
- Giao điểm của ba đường trung tuyến được gọi là trọng tâm của tam giác.
Ví dụ: Với G là trọng tâm của ΔABC ta có:
2. Bài tập minh họa
Câu 1: Cho ΔABC, AC > AB. Gọi BE và CD là các trung tuyến. Chứng minh: CD > BE.
Hướng dẫn giải
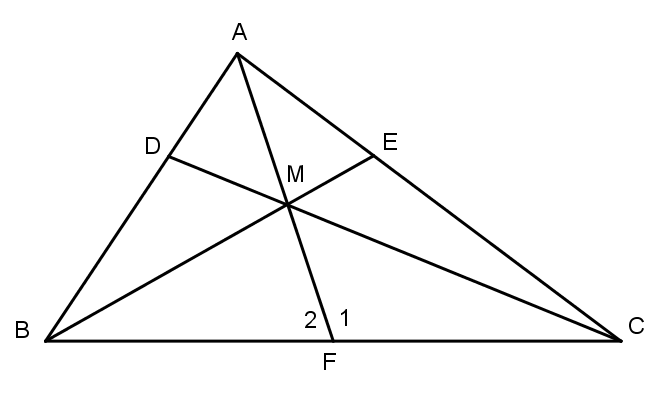
Gọi F là trung tuyến của BC thì ba đường trung tuyến AF, BE, CD cắt nhau ở M. Vì AC > AB nên ^F1>^F2 (do ΔAFB và ΔAFCcó AF cạnh chung, FB = FC và AC > AB)
Từ ^F1>^F2từ hai tam giác MFB và MFC có: MF cạnh chung, FB = FC ta suy ra MC > MB.
Hay 23CD>23BE. Vậy CD > BE.
Câu 2: Cho hai đường thẳng x’x và y’y cắt nhau ở O. Trên tia Ox lấy hai điểm A và B sao cho A nằm giữa O và B, AB = 20A. Trên y’y lấy 2 điểm L và M sao cho O là trung điểm của đoạn thẳng LM. Nối B với L, B với M và gọi là P là trung điểm của đoạn thẳng MB, Q là trung điểm của đoạn thẳng LB. Chứng minh các đoạn thẳng LP và MQ đi qua A.
Hướng dẫn giải
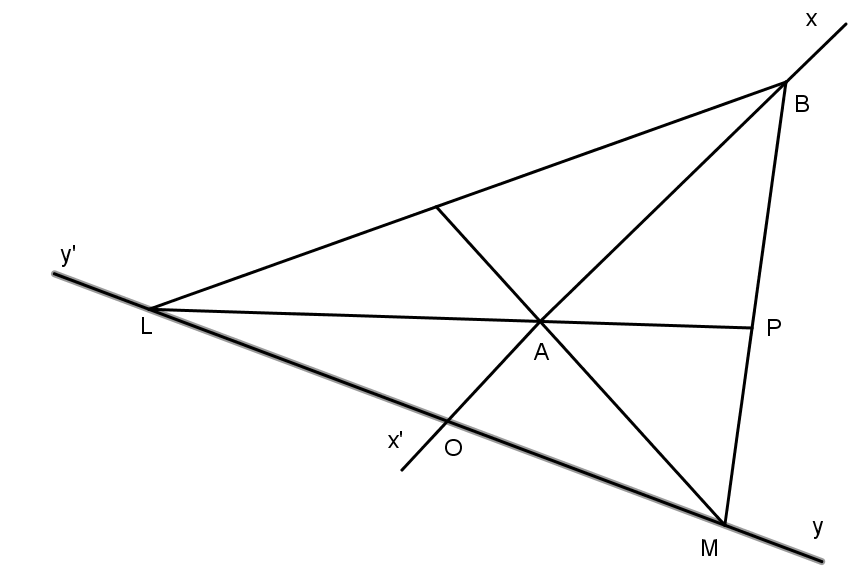
Ta có O là trung điểm của LM (gt)
Suy ra BO là đường trung tuyến của ΔBLM(1)
Mặt khác BO = BA + AO vì A nằm giữa O, B hay BO = 2AO + AO = 3AO vì AB =2AO (gt)
Suy ra AO=13BOhayBA=23BO(2)
Từ (1) và (2) suy ra A là trọng tâm của ΔBLM (tính chất của trọng tâm)
Mà LP và MQ là các đường trung tuyến của ΔBLM vì P là trung điểm của đoạn thẳng MB (gt) và O là trung điểm của đoạn thẳng LB (gt)
Suy ra các đoạn thẳng LP và MQ đều đi qua A (tính chất 3 đường trung tuyến).
Câu 3: Kéo dài trung tuyến AM của ΔABC một đoạn thẳng MD có độ dài bằng 13 độ dài AM. Gọi G là trọng tâm của ΔABC. So sánh các cạnh của ΔBGD với các trung tuyến của ΔABC.
Hướng dẫn giải
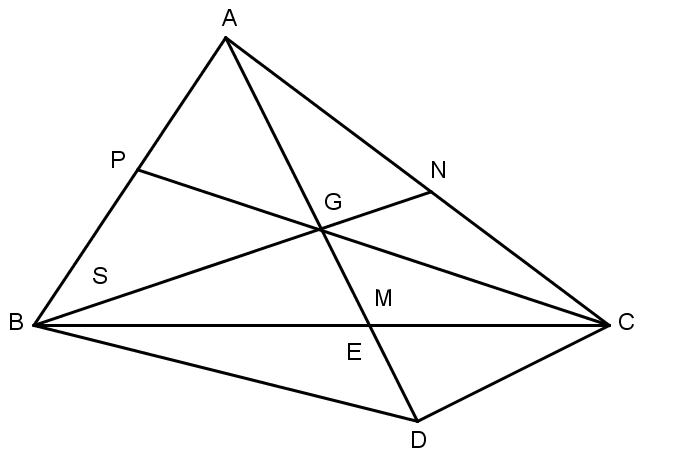
Gọi N, P lần lượt là trung điểm của AC, AB.
Ta có AM, BN, CP cắt nhau tại G(tính chất đường trung tuyến) và có
BG=23BN;CG=23CP;AG=23AM.
ΔBMG=ΔCMD(c.g.c)⇒GB=DCΔGMC=ΔDMB(c.g.c)⇒GC=DB
Xét ΔBGD và ΔCDG có:
GB = DC
BD = DG
GD cạnh chung
Nên ΔBGD=ΔCDG(c.c.c)⇒BD=CG=23CP
Ta cũng có: GD=23AM
Ta có ΔBGD có các cạnh lần lượt bằng 23 các trung tuyến của ΔABC
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Cho ΔABC có BM, CN là hai đường trung tuyến cắt nhau tại G. Kéo dài BM lấy đoạn ME = MG. Kéo dài CN lấy đoạn NF = NG. Chứng minh:
a) EF = BC
b) Đường thẳng AG đi qua trung điểm BC.
Câu 2: Cho ΔABC. Trên cạnh BC lấy điểm T sao cho TB=23BC. Trên tia đối của tia CA lấy điểm D sao cho CD = CA. Đường thẳng DT cắt cạnh AB tại E. Chứng minh EA = EB.
Câu 3: Cho ΔABC,BC=a,CA=b,AB=c. Kẻ trung tuyến AM. Đặt AM=ma.
Chứng minh rằng: b+c−a2<ma<b+c2
3.2. Bài tập trắc nghiệm
Câu 1: Trong tam giác ABC có trung tuyến AM = 9cm và trọng tâm G. Độ dài đoạn AG là
A. 4,5cm
B. 3cm
C. 6cm
D. 4cm
Câu 2: Chọn câu sai:
A. Trong một tam giác có ba đường trung tuyến
B. Các đường trung tuyến của tam giác cắt nhau tại một điểm
C. Giao của ba đường trung tuyến của một tam giác gọi là trọng tâm của tam giác đó
D. Một tam giác có hai trọng tâm
Câu 3: Cho hình vẽ sau:

Điền số thích hợp vào chỗ chấm: BG = ...BE
A. 2
B. 3
C. 13
D. 23
Câu 4: Điền số thích hợp vào chỗ chấm: "Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng...độ dài đường trung tuyến đi qua đỉnh ấy"
A. 23
B. 32
C. 2
D. 3
Câu 5:
Cho hình vẽ sau:

Điền số thích hợp vào chỗ chấm: AG = ...GD
A. 2
B. 3
C. 13
D. 23
4. Kết luận
Qua bài học này, các em cần nắm được những nội dung sau:
- Nắm được định nghĩa, tính chất của đường trung tuyến trong tam giác.
- Áp dụng giải các bài toán có liên quan.
Tham khảo thêm
- doc Toán 7 Chương 3 Bài 1: Quan hệ giữa góc và cạnh đối diện trong một tam giác
- doc Toán 7 Chương 3 Bài 2: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
- doc Toán 7 Chương 3 Bài 3: Quan hệ giữa ba cạnh của một tam giác Bất đẳng thức tam giác
- doc Toán 7 Chương 3 Bài 5: Tính chất tia phân giác của một góc
- doc Toán 7 Chương 3 Bài 6: Tính chất ba đường phân giác của tam giác
- doc Toán 7 Chương 3 Bài 7: Tính chất đường trung trực của một đoạn thẳng
- doc Toán 7 Chương 3 Bài 8: Tính chất ba đường trung trực của tam giác
- doc Toán 7 Chương 3 Bài 9: Tính chất ba đường cao của tam giác