Toán 7 Chương 2 Bài 1: Tổng ba góc của một tam giác
Elib đã biên soạn và tổng hợp để giới thiệu đến các em nội dung bài giảngTổng ba góc của một tam giác. Bài giảng giúp các em nắm vững lý thuyết bài học, kèm theo đó là những bài tập minh họa có hướng dẫn giải chi tiết sẽ giúp các em hiểu bài hơn. Mời các em cùng theo dõi.
Mục lục nội dung

Toán 7 Chương 2 Bài 1: Tổng ba góc của một tam giác
1. Tóm tắt lý thuyết
1.1. Tổng ba góc của một tam giác
Định lý: Tổng ba góc của một tam giác bằng
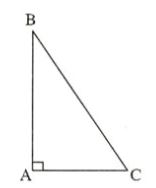
1.2. Áp dụng vào tam giác vuông
Định lý: Trong một tam giác vuông hai góc nhọn phụ nhau.
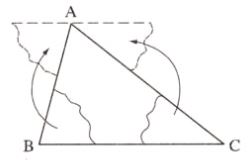
1.3. Góc ngoài của tam giác
Định nghĩa: Góc ngoài của một tam giác là góc kề bù với một góc của tam giác ấy.
Định lý: Mỗi góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó.
Nhận xét: Góc ngoài của tam giác bằng tổng của hai góc trong không kề với nó.
2. Bài tập minh họa
Câu 1: Trong các hình a, b, c hình nào ghi số đo sai?
.jpg)
Hướng dẫn giải
Tổng ba góc của tam giác trong hình a là:
Nên hình a ghi số đo sai.
Tổng ba góc của tam giác trong hình b là:
Nên hình b ghi số đo đúng.
Tổng hai góc trong của tam giác trong hình c là khác với góc ngoài, không kề với chúng là
Vậy hình c ghi số đo sai
Câu 2: Cho điểm O trong tam giác ABC. Chứng minh rằng
Hướng dẫn giải
Kéo dài BO cắt AC tại D.
Ta có
(Vì là góc ngoài của )
Mặt khác:
(vì là góc ngoài của )
Suy ra
Vậy
Câu 3: Cho tam giác ABC có Tia phân giác của góc B cắt AC cắt ở D. Tính
Hướng dẫn giải
.jpg)
Xét tam giác ABC có
Do BD là tia phân giác của góc B nên
Suy ra
Vậy
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Cho tam giác ABC có Gọi Am là tia phân giác của góc ngoài ở điểm A. Hãy chứng minh tỏ rằng Am// BC.
Câu 2: Chứng minh rằng tổng ba góc ngoài của một tam giác bằng 4 vuông.
Câu 3: Tìm số đo các góc của tam giác ABC biết rằng:
3.2. Bài tập trắc nghiệm
Câu 1: Cho tam giác ABC vuông tại A. Khi đó
A.
B.
C.
D.
Câu 2: Cho tam giác ABC có . Số đo góc B là
A. 340
B. 350
C. 600
D. 900
Câu 3: Cho tam giác có ba góc bằng nhau. Tính số đo mỗi góc
A. 400
B. 500
C. 600
D. 700
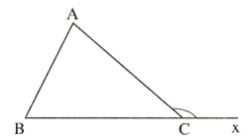
Câu 4: Cho hình sau. Tính số đo x
.jpg)
A. 900
B. 1000
C. 1200
D. 1400
Câu 5: Cho tam giác ABC biết rằng số đo các góc tỉ lệ với 2, 3, 4. Tính số đo góc B
A.
B.
C.
D.
4. Kết luận
Qua bài học này, các em cần đạt được những mục tiêu sau:
-
Định lí tổng 3 góc trong một tam giác.
-
Định nghĩa, tính chất góc ngoài trong một tam giác.
Tham khảo thêm
- doc Toán 7 Chương 2 Bài 2: Hai tam giác bằng nhau
- doc Toán 7 Chương 2 Bài 3: Trường hợp bằng nhau thứ nhất của tam giác cạnh - cạnh - cạnh (c-c-c)
- doc Toán 7 Chương 2 Bài 4: Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh (c-g-c)
- doc Toán 7 Chương 2 Bài 5: Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc (g-c-g)
- doc Toán 7 Chương 2 Bài 6: Tam giác cân
- doc Toán 7 Chương 2 Bài 7: Định lí Py-ta-go
- doc Toán 7 Chương 2 Bài 8: Các trường hợp bằng nhau của tam giác vuông