Toán 7 Chương 3 Bài 3: Quan hệ giữa ba cạnh của một tam giác Bất đẳng thức tam giác

Định lý: Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng nhỏ hơn độ dài cạnh còn lại.

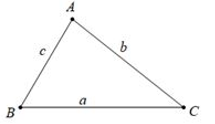
Ví dụ: Cho tam giác ABC, ta có các bất đẳng thức sau:

• AB + AC > BC hay b + c > a
• AB + BC > AC hay c + a > b
• AC + BC > AB hay b + a > c

Hệ quả: Trong một tam giác, hiệu độ dài hai cạnh bất kì bao giờ cũng nhỏ hơn độ dài cạnh còn lại.

Ví dụ: Cho tam giác ABC, ta có các bất đẳng thức sau:

• |AB - AC| < BC hay |b - c| < a
• |AB - BC| < AC hay |c - a| < b
• |AC - BC| < AB hay |b - a| < c

Nhận xét: Trong một tam giác, độ dài một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng các độ dài của hai cạnh còn lại

Ví dụ: Trong tam giác ABC, với cạnh BC ta có:

|AC - AB| < BC < AC + AB hay |b - c| < a < b + c

Câu 1: Cho điểm D nằm trên cạnh BC của \(\Delta ABC\). Chứng minh rằng:

\(\frac{{AB + AC - BC}}{2} < AD < \frac{{AB + AC + BC}}{2}\)

Hướng dẫn giải

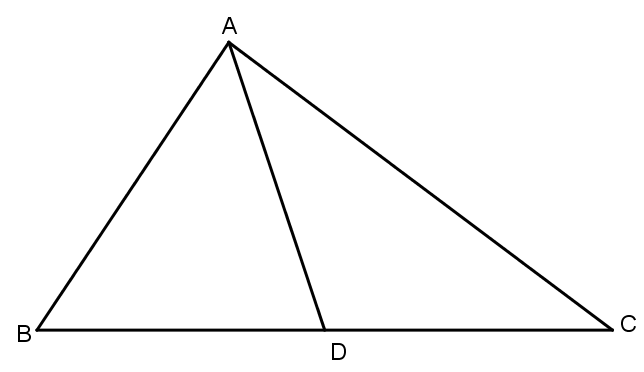
Trong \(\Delta ABD\) ta có:

\(AB - BD < AD < AB + B{D^{\,\,(1)}}\)

Trong\(\Delta ACD\) ta có:

\(AC - DC < AD < AC + DC\,{\,^{(2)}}\)

Cộng (1) và (2) ta được:

AB + AC – BD – DC < 2AD < AB + AC + BD + DC

Hay AB + AC – BC < 2AD < AB + AC + BC

Vậy \(\frac{{AB + AC - BC}}{2} < AD < \frac{{AB + AC + BC}}{2}\)

Câu 2: Một tam giác có hai cạnh dài 2cm và 10cm. Tìm số đo cạnh thứ ba, biết rằng số đo ấy là một số nguyên tố.

Hướng dẫn giải

Giả sử cạnh thứ ba dài x(cm). Áp dụng bất đẳng thức trong tam giác ta c\(10{\rm{ }} - {\rm{ }}2 < x < 10 + 2 \Rightarrow 8 < x < 12\)

Vì x là số nguyên tố lớn hơn 8 và nhỏ hơn 12 nên x = 11

Vậy số đo cạnh thứ ba là 11cm.

Câu 3: Cho \(\Delta ABC,M\) là một điểm tuỳ ý ở miền trong \(\Delta ABC\). Chứng minh: \(MB + MC < AB + AC\)

Hướng dẫn giải

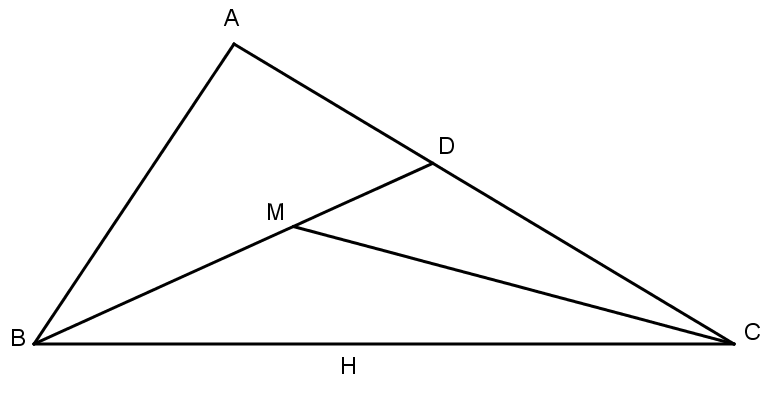
Vì M thuộc miền trong \(\Delta ABC\) nên tia BM thuộc miền trong \(\widehat B\), nó cắt cạnh AC tại D.

D nằm giữa A và C, M nằm giữa B và D.

Trong \(\Delta BAD\) có:

\(BM + MD < BA + AD\,{\,^{(1)}}\)

Trong \(\Delta MDC\) có: \(MC - MD < DC{\,^{\,(2)}}\)

Cộng 2 vế của (1) và (2) với nhau ta được:

BM + MC < BA + AD + DC

Hay BM + MC < BA + AC.

Câu 1: Hãy tìm độ dài của cạnh của một tam giác, biết cạnh thứ nhất dài gấp rưỡi cạnh thư hai, cạnh thứ nhất dài gấp rưỡi cạnh thứ ba và nửa chu vi tam giác bằng 9,5cm.

Câu 2: Cho \(\Delta ABC\)có AC > AB. Nối A với trung điểm M của BC. Trên tia AM lấy điểm E sao cho M là trung điểm của đoạn  thẳng AE. Nối C với C.

a) So sánh hai đoạn thẳng AB và CE.

b) Chứng minh: \(\frac{{AC - AB}}{2} < AM < \frac{{AC + AB}}{2}\)

Câu 3: Cho điểm M nằm trong \(\Delta ABC.\) Chứng minh rằng tổng MA + MB + MC lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của \(\Delta ABC.\)

Câu 1: Cho tam giác ABC có AB>AC. Kẻ tia phân giác AD của góc A (D thuộc BC). Trên đoạn AD lấy một điểm E tùy ý. Hãy chọn khẳng định đúng.

A. AB−AC>EB−EC

B. AB−AC<EB−EC

C. AB−AC=EB−EC

D. Cả 3 đáp án trên đều sai

Câu 2: Cho tam giác ABC biết AB = 1cm, BC = 9cm và cạnh AC là một số nguyên. Chu vi tam giác ABC là:

A. 17cm

B. 18cm

C. 19cm

D. 16cm

Câu 3: Cho tam giác ABC có BC=1cm, AC=8cm và độ dài cạnh AB là một số nguyên (cm). Tam giác ABC là tam giác gì?

A. Tam giác vuông tại A

B. Tam giác cân tại A

C. Tam giác vuông cân tại A

D. Tam giác cân taị B

Câu 4: Dựa vào bất đẳng thức tam giác, kiểm tra bộ ba nào trong các bộ ba đoạn thẳng có độ dài cho sau đây không thể là ba cạnh của một tam giác

A. 3cm, 4cm, 7cm 

B. 4cm, 5cm, 6cm 

C. 2cm, 5cm, 7cm 

D. 3cm, 6cm, 5cm 

Câu 5: Cho tam giác ABC có cạnh AB= 1cm và cạnh BC=4cm. Tính độ dài cạnh AC biết độ dài cạnh AC là một số nguyên 

A. 1cm 

B. 2cm

C. 3cm

D. 4cm

Qua bài học này, các em cần nắm được những nội dung sau:

• Hiểu được bất đẳng thức trong tam giác.
• Áp dụng làm được các bài toán liên quan.